|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faith C. — Rings and Things and a Fine Array of Twentieth Century Associative Algebra |
|
|
 |
| Предметный указатель |
Cedo example 12.13f
Cedo theorem 6.33—6.34
Cedo — Herbera theorem 9.7
Cedo, Ferran 309
Center 2.5s
centralizer 2.5Cs
CF ring 13.31s
CFPF ring 5.12
Chain module 5.1A'f 16.46s
Chain ring (= valuation ring) 3.15As
Chain, ascending Loewy 3.33As
Chain, composition 2.17Cs
Chain, equivalent 2.17Fs
Chain, refinement of 2.17C
Chandra, Harish 282—283
Chandra, Lily 282
Change of rings theorem 14.8A 14.8B 14.8C
Character module 4.Bs
Characteristic equation 2.6B
Chase 24 87 95 110 218 245 253
Chase theorem 1.17A 3.4D—3.4E 6.6
Chase — Faith Theorem 4.6
Chase, Stephen ("Steve") 278 299
Chatters 189 211
Chatters module 7.21s
Chatters theorem 7.1—7.2 7.21
Cheatham 90
Cherlin theorem 3.43As
Cherlin, Chantal xxix
Cherlin, Gregory xxix 260 266n 285
Chevalley 23 85 101 179—180
Chevalley theorem 2.6 2.6ff 9.19(4)
Chevalley, C. 277
Chihara, Theodore ("Ted") 261
Chinese remainder theorem (reference) 5.1A'f
Clark 101 104
Classical Krull dimension 14.1A 14.24
Classical quotient ring 3.12Bf 3.6As 6.26 7.35ff
Classical right quotient ring ( ) 3.12Bf 6.36 7.35s ) 3.12Bf 6.36 7.35s
Classical valuation ring 9.15B
Clements, Samuel see "Mark Twain"
Clements, Susy 295
Closed (essential) ideal 4.11
Closed ideal 4.11
Clouseau, "Inspector" 294
Co-faithful 3.9 6.32As
Co-faithful module 3.9 3.62As
Co-Noether (also Noetherian) 7.49
Cogenerator module 3.3'
Cogenerator ring 3.3' 4.23A
Cogenerator, minimal 3.3'f
Cohen — Montgomery theorem 12.F
Cohen — Ornstein theorem 2.19B
Cohen, I. theorem 2.19A
Cohen, I.S. 105 108 110
Cohen, M. 183
Cohen, M. theorem 12.A
Cohen, Miriam 289
Cohen, Paul J. 273—274
Coherent ring 6.6
Cohn 10—12 16 23 24 67 90 121 197 22—223 225—226
Cohn pure module 6.As
Cohn pure submodule 6.As
Cohn theorem 2.7s 6.24 6.31
Cohn — Bergman theorem 9.26C
Cohn, Paul Moritz 283 299
Cohn, Richard Moses ("Dick") 283
Colby 160
Colby theorem 6.8—6.9
Cole (Prize) 282
Compact faithful module 3.9 3.62As
Complement direct summands (cds) 8.6s
Complement right ideal 3.2Es
Complement submodule 3.2Es
Complement, maximal 13.14B
Complemented lattice 12.4s
Complete local ring 5.4B
Complete, maximally 5.14As
Completely primary ring 5.1A's
Completely sigma  injective 7.32s 7.32—7.34 injective 7.32s 7.32—7.34
Completion of a local ring 5.4B
Completion, p-adic 5.4B 13.4C
Composition series 2.17F
Conch subring 9.10s
Conch, an element 9.10s
Conjugate subring 2.5Cs
Connell theorem 11.1—11.4 11.9—11.10
Connell, Ian 292
Cononsingular ring 12.0As
Continuous geometry 12.4s
Continuous module 12.4C's
Continuous ring 12.4As
Corner theorem 1.16
Correl, Ellen 260
Cotorsion-free 1.16A
Couchot theorem 6.7B—6.7C
Courter theorem 12.0B
Courter, Dick 283
Cover, projective 3.30s
Cowling, Vincent 299
Cox 198
Cox theorem 13.23
Coxeter, H.M.S. 291
Cozzens 66 69 143 149 197
Cozzens V-domains 3.20f
Cozzens — Faith theorem 2.6F
Cozzens, John 258 286—287 303 312
Cozzens, Margaret ("Midge") 286
Crawley — Jonsson theorem 8.3
Critical composition series 14.33s
Critical quotients 14.33s
Critical submodule 14.33s
Croisot 62 77 179 227
Croisot, Robert 284
Crossed product 2.5Bff
CS module 12.4s
CS ring 12.4s
CS, quotient 12.4C
Curie, Pierre 321
Curtis 18 49
Cyclic algebra 2.5Bff
Cyclic group 1.6
Cyclic presented 6.5As
Cyclic, sigma 5.1As
D see "Dual"
D-ring see "Dual"
Dade 176 185
Dade theorem 3.17 11.11ff
Dales, H.G. 260
Damiano — Faith theorem 3.18C
Davis 164—165
Davis theorem 9.9 9.29
Decomposable module 1.2
Dedekind see §17
Dedekind finite ring 4.6A 4.6A'
Dedekind independence theorem 17.0
Dedekind infinite 4.6B
Dedekind ring 9.29s
Degree, bounded 5.1
Dehn 221
Dehn definition 15.1
Deligne theorem 1.31B
Delta ( ) injective module 3.10A 7.45s 13.4E ) injective module 3.10A 7.45s 13.4E
Delta ( ) ring 7.47s ) ring 7.47s
DeMeyer 99 245
Dense right ideal 9.27s §12
Dense ring of linear transformations 2.6 3.8A
Dense rings of linear transformations (l.t.'s) 2.6 3.8A
Density theorem, Chevalley — Jacobson 2.6 3.8A
Dependence theorem 17.1
| Derivation 1.32B
Derivation, inner 2.5f
Desargues 23
Deskins, Barbara 262
Deskins, W.E. ("Cupcake") 261 262
Dewey, Thomas 298
Dicks 124 130 159—160
Dicks — Menal theorem 3.24B
Dicks, Warren 308—309
Dickson theorem 2.5f—2.6s
Dickson, L.E. 15 19 23
Dickson, Leonard E. 258
Dickson, S.E. 184
Dickson, S.E. theorem §13
Dieudonne 24 69
Differential polynomial ring 3.20f 7.15s
Differential, ordinary 7.15s
Dikranjan 194
Dimension of a prime ideal 2.22s
Dimension, global 14.3s
Dimension, Goldie 3.13s
Dimension, homological 14.3s
Dimension, injective 14.3s
Dimension, Krull 14.1 A 14.24 14.26 14.28s
Direct factor (= summand) 1.1—1.4 2.0ss
Direct product 1.1
Direct sum 1.1
Direct summand 1.1—1.4
Directly finite ring 4.6A
Dischinger 103
Discrete Pruefer ring 9.35f
Discrete ring (= skew field) 2.0s
Discrete valuation domain 6.46f 9.28s
Divisible group 1.10
Division algebra 2.0s 2.7ss
Dixmier 218
Dixmier theorem 14.47
Dlab 254
Dlab — Ringel theorem 13.30A—13.30D
Dlab, V. 287
Dobbs 137
Dold, Albrecht ("Al") 264 277
Domanov 98
Domanov theorem 11.9'
Domination of a local ring 9.18
Domination of local ring 9.18
Donnelly, Sarah xxix
Drazin 30 101
Dual (D) ring 13.12s
Dual module 1.5
Dual ring 13.12s
Duality context 13.1s
Duality functor 13.1s
Duality, inverse of 13.1a
Duality, Morita 13.1s
Dubois theorem 1.20
Dugas — Goebel theorem 1.16A 1.16B
Dukas, Helen 279
Dung 189 see
Durkheim, Emil 275
Dyer-Bennet, John 259
Dyson 48
Dyson, Freeman 271 278 283 301 314n
Dyson, Ima 283
E-reflexive module 13.1s
Eakin 184 245
Eakin theorem 10.5—10.7
EC see "Existentially closed"
Eckmann — Schoepf theorem 3.2D
Eckmann, Beno 277
Eckstein 49
Eddy, Captain 287
Eggert 170—171 191
Eggert theorem 9.31
Ehrlich 28 89
Ehrlich theorem 4.3As 6.3B
Eilenberg 52 54 77 206—207 218
Eilenberg theorem 3.4
Eilenberg, Samuel ("Sammy") 262 312—314 320
Einstein, Albert 279—280 286 314 316
Eisenbud 37 72 114 184 229
Eisenbud — Griffith theorem 5.3A—5.3B
Eisenbud, David 312
Eklof — Sabbagh theorem 6.20
Elementary divisor ring (= EDR) 3.6Bs
Elementary equivalent 6.43
Elliott 127
Elliott, Joanne 299
Embedding of a group (module) 3.3s
Endo 117—118 245
Endo theorem 4.A1 4.27—4.28 5.40 9.24(4)
Endomorphism ring 1.2
Epimorphism, flat 12.3 12.14
Epimorphism, module 3.0
Epimorphism, ring 12.1
Equivalence chains 2.17Fs
Equivalence of categories 3.51f
Equivalence, Morita 3.51f
Equivalent categories 3.51f
Erdoes, Paul 290—291
Erikson, Erik 272n
Ernest, John A. 276
Essential extension 3.2Ds
Essential submodule 3.2Ds
Euclid 316 323
Evans 158
Evans theorem 6.3F 8.G
Exact sequences 14.3s
Exchange finite exchange property 8.3s
Exchange module 8.3s
Exchange property 8.3s
Exchange ring 8.4As
Existentially closed (= EC) rings 6.20s
Existentially closed sfields 6.24
F-semiperfect ring 6.52s
f.e. see "Finitely embedded"
Facchini 64 159 239
Facchini theorem 5.4E 6.17—6.18 8.8f 9.36 9.37 13.11B
Facchini — Faith theorem 6.4
Facchini, Alberto 309—310
Factor set 2.5Bff—2.6ss
Faith theorem 1.32A 2.10—2.12 2.15A—2.15B 2.16C—2.16D 2.371 3.5C 3.7A—3.7B 4.4 4.19B—4.19D 4.25 4.29—4.31 5.27—5.35 5.38 5.41—5.42 5.44—5.45 5.48 5.52—5.56 6.30 6.39 7.32—7.34 7.38—7.47 9.4—9.6 9.13—9.15 9.34 12.6 13.31 13.42—13.43 16.15 16.19—16.20 16.24 16.27—16.32 16.34—16.37 16.40—16.45 16.50 §17
Faith — Herbera theorem 8.8ff 13.10
Faith — Menal theorem 13.18—13.20 13.37A—13.37B 13.38
Faith — Utumi theorem 4.2A 3.9D 7.6 3.9D
Faith — Walker Theorem 3.5A 3.5B 3.5D 8.2A 8.2B 13.33
Faith, Carl 253ff
Faith, Cindy 261 270 302
Faith, Eldridge 258—259
Faith, Frederick 257
Faith, Heidi 261 270 276—277 296
Faith, Herbert Spencer ("Dad") 258
Faith, Vila Belle Foster ("Mama") 256
Faith-Herbera 159
Faithful Modulle 2.6s
Falk, Rick 258
Farkas 178
Farkas — Snider theorem 12.C
Faticone theorem 5.46 5.48
Faticoni 104 117
Faticoni, Theodore ("Ted") 306 307 307n
Faulkner, William 324
FBM (finite bounded module type) ring 8.8ff
Feit, Walter 301
Fermat, Pierre 318 323
Feynman, Richard 281
FFM (finite module type) ring 8.8ff 11.11ff(p.177)
FGC classification theorem 5.11
FGC ring 5.1 As
FGF ( modules modules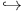 freebees) ring 13.31s freebees) ring 13.31s
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)  injective
injective  ) injective module
) injective module  modules
modules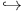 freebees) ring
freebees) ring