|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faith C. — Rings and Things and a Fine Array of Twentieth Century Associative Algebra |
|
|
 |
| Предметный указатель |
Field formally real 1.30 1.40s 2.39s
Field ordered 1.30
Field splitting 2.5Bff—2.6ss 2.51
Field, absolutely algebraic 1.28 2.40s
Field, algebraic 1.28
Fieldhouse 91
Fieldhouse, David 292
Findlay 169 180
Findlay — Lambek theorem 9.27s §12
Fine, Nathan 260
Finite basis of a module 1.1
Finite fractions 9.28s
Finite representation type see "FFM"
Finitely embedded (= f.e.) module 3.58s
Finitely embedded ring 3.58s 7.8s 7.8ff
Finitely generated (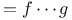 ) module 1.1 ) module 1.1
Finitely generated (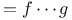 ) ring 2.21A 2.21Af ) ring 2.21A 2.21Af
Finitely PF (= FPF) ring 4.26ff
Finitely presented ( ) module 6.As ) module 6.As
Finitely pseudo-Frobenius (= FPF) 4.26s
Fisher 225
Fisher — Osterburg theorem 12.D(1) 12.D(1)
Fisher — Snider theorem 4.12
Fisher, B. 301
Fisher, Louis 296 317
Fitting 38 86 105
Fitting lemma 3.64—3.66 8.8f
Fitting theorem 3.38 3.69 5.1A'f
Fitzgerald, F. Scott 317
Flat embedding 3.16C 16.33
Flat epimorphism 12.3 12.14
Flat module 4.As
Flexner, Abraham 270 278 281 316
Fontana 171
Formanek 98 178 224 227
Formanek — Jategoankar theorem 12.G
Forsythe 94
Fossum 168
Fossum — Griffith — Reiten theorem 4.25
Foster, Vila Belle ("Mama") 256
Fp-injective module 6.As
FP-injective ring 6.Es 6.Bs
FPF see "PF"
FPF (= finitely pseudo Frobenius) product theorem 5.28
FPF ring 4.26s see
FPF ring theorem 5.42
FPF split-null extension 5.41
Fractionally FP-injective 6.4s
Fractionally self-injective (= FSI) 5.9s
Fraenkel, A. 313
Franco 310
Frattini 71
Frattini subgroup 3.34s
Fred see "Faith"
free see "Algebra"
Free algebra 15.15
Free basis 1.1
Free direct summands 3.79 5.34s
Free module 1.1 3.1As
Free rank 5.34s
Free rank of a module 5.34s
Free ring 14.15(4)
Freud 276
Freyd 52 77
Friend, David 290n
Frink, Aileen 262
Frink, Orrin 262 277
Frobenius 5 2.0
Froeschl theorem 9.15C
FSFPI ring 6.4
Fuchs 6 69—70 122 135 157 166
Fuchs — Salce theorem 6.19 9.13f
Fuchs — Salce — Zanardo theorem 9.46A
Fuchs — Szele theorem 1.26A
Fuelberth — Teply theorem 4.1F
Fulbright 263 303 308 314
Fuld, Mrs. Felix 273
Fuller 59 70 77—78 161 254 see
Fuller theorem 5.2E 6.57
Fuller, Kent R. 287
Fully bounded Noetherian (FBN) ring 3.36Es 15.17s
Fully bounded ring 3.36Es
Fully invariant submodule 1.3
Fussell, Paul 269
Gabriel 52 90 181 184 211 218
Gabriel theorem 4.Cf 12.1s 14.27 14.28A 14.28B
Gaddis, John Lewis 272
Gaerding, Lars 269
Galois ix
Galois group 2.7ss
Galois subring (= fixring) 2.7ss 17.0ff
Galois theory 2.7
Galois, Evariste 256
Gambill, Robert ("Bob") 260
Gandhi ("Mahatma") 283 295
Gangiolli, Minoto 283n
Gaudi, Antonio 311 321
Gauss 132
Gauss theorem 1.28C(2)
Gauss, Karl Friedrich 255
Gelfand, I.M. 302
General Wedderburn theorem 3.51ss
Generalized Dedekind ring 9.36s
Generalized principal ideal theorem 2.23
Generated, 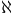 1.1 3.1B 1.1 3.1B
Generated, countably 1.1
Generated, finitely 1.1
generator function 1.32A
Generator of a category 3.3f
Generator of a field 1.28ff 1.32A
Generator of a group 1.6
Generator of a module 1.1
Generator of mod-R 3.3f
Generic division algebra 15.16f
Generic matrix ring 15.15
Generic product of rings 5.23As
Gentile 174
Gentile theorem 13.39—13.40
Genus of a module 5.22f
Genus, big 5.22f
Genus, little 5.22f
Geometry, continuous 12.4s
Geometry, projective 12.4As
Geramita, Anthony Vito 304—305
Gill 111
Gill theorem 5.1 5.4D 5.16
Gillman, Leonard ("Lenny") 260
Gillman, Reba 260
Gilmer 171
Gilmer theorem 9.19 9.35f 16.8B—16.8C
Gilmer — Heinzer theorem 9.19(5)
Ginn 198
Ginn — Moss theorem 7.8
Global dimension 14.3s
Global dimension theorem 14.12
Goedel, Kurt 273 281 318
Golan, Hembda 288
Golan, Jonathan 288
Goldie 63 74 77 79 179—181 227 238
Goldie dimension 3.13s 16.9B 16.16
Goldie ring 3.13
Goldie theorem 3.13
Goldie — Small theorem 14.31A
Goldie, Alfred 284—285 299
Goldman 72 99 185 243 253 see
Goldman theorem 3.36 3.36B
Goldstine, Herman 281
Golod 74
Golod — Shafarevitch theorem 3.43As
Gomez Pardo 135
| Gomez Pardo theorem 13.31 (10)
Gomez Pardo — Guil Asensio theorem 12.8A 13.34—13.35
Gonshor, Harry 283
Goodearl 77 94—95 97—98 123 130 141 143 158 174 182 187 193 215 242
Goodearl theorem 4.1G 4.1K 4.2C 4.8—4.9 4.11 14.15.9—14.15.11
Goodearl — Handelman theorem 4.8
Goodearl — Moncasi theorem 6.31
Goodearl — Warfield theorem 6.3H
Goodearl — Zimmermann — Huisgen theorem 14.41—14.45
Goodearl, Kenneth ("Ken") 303 309
Goodearl-Warfield 17 22 72—74 80 212—214
Goodman, Adolph W. 255 292
Gopalakrishnan 209
Gorbachev, Mikhail 272
Gordon 71 74 211
Gordon theorem 3.34A(2) 14.33
Gordon — Robson theorem 14.29A 14.29B 14.30—14.31 14.43s
Gorenstein, Daniel ("Danny") 299 300—303 315
Gorenstein, Helen 302—303
Gorenstein, Julia 303
Gould, S.H. 256 291
Goursaud 61—62
Goursaud theorem 13.7A
Govorov 68
Govorov — Lazard theorem 4.A
Grad, Arthur 300
Graves, Robert 323
Green 210
Greenberg — Vasconcelos theorem 14.20
Grell 85
Griffin 165 170—171 191
Griffin theorem 9.12 9.30 9.33
Griffith 55 110 165 see
Griffith — Eisenbud theorem 3.5Af
Grobman, Arnold 285
Groethendieck 100 184
Groethendieck theorem 4.16As
Groethendieck, Alexandre 301
Gross, Mason 286
Group algebra 2.39—2.40
Group rings §11
Group, abelian 1.6—1.21
Group, bounded order 1.8—1.9 1.14
Group, circle 17.1ss
Group, divisible 1.10—1.13
Group, free 3.24A 3.24B 3.74r6
Group, Galois 2.7s
Group, general linear 3.74s
Group, locally finite 11.9 12.0C
Group, polycyclic by finite 11.12
Group, primary 1.7
Group, reduced 1.11f
Group, torsion 1.6 1.14
Group, torsionfree 1.6
Gruson 210
Guil see "Asensio"
Gulliksen 215—216
Gupta theorem 4.2B
Gupta, Ram 292
Guy, Arthur 279—280
Guy, Dorothy 279—280
Guy, Jennifer 280n
Hadamard, Jacques 317
Hajarnavis 189 211
Hajarnavis — Norton theorem 13.16—13.17
Hale, Jack 260
Hall theorem 2.50f
Hall, M. 48 78 94
Hall, P 178
Halmos, Paul 281
Halperin, I. 291
Hamilton 15 21 2.0s
Hamilton — Cayley theorem 2.6B
Hamiltonian group 3.75s
Hamsher theorem 3.32f
Handelman 97 123 190
Handelman — Goodearl theorem 4.8
Handelman — Lawrence theorem 12.13
Hannah 97
Hansen theorem 3.11A
Harada 158 219
Harada theorem 3.9D 13.9D 4.1A
Harada — Ishii theorem 3.8B
Harada, K. 301
Harcenko (Kharchenko) 45 130
Harcenko theorem 12.A 12.B
Hardy, Thomas 265
Harmani 30
Harrison 24
Hart 77 214
Hartley 176
Hartley — Pickel theorem 3.76
Hartley, Brian 309
Hasse 19
Hauger 143
Hausdorff 31
Hazard, Clifton 259
Heaton, Bob 283
Heidi see "Faith"
Heinzer 72 127
Heinzer theorem 10.5—10.7
Heitman 123
Heitman — Levy theorem 6.3Bf
Henriksen theorem 2.16H 4.7D 6.3D
Henriksen, Melvin 260 286n 290
Hensel 85 154
Henselian ring 8.Gs
Heraclitus 296n
Herbera 101 104 112 159 160 169 197
Herbera theorem 3.6B—3.6E 4.17A 6.14 8.8ff 9.7
Herbera — Shamsuddin theorem 8.C
Herbera — Xue theorem 6.15
Herbera, Dolors 306 308—309
Hermite ring 6.3Bs
Herstein 18—19 26—28 30 43 47 71 75 223—225
Herstein theorem 2.15Af 2.16Js 2.38D 2.44—2.47
Herstein — Small theorem 2.38C 3.41—3.42
Herstein, Israel ("Yitz") 277 286 301 304 315
Herzog 160 205
Herzog theorem 16.58
Herzog, Fritz 262
Higgins 74
Higman 74 160 177
Higman problem 11.11f
Higman theorem 3.43Ass 11.11ff
hilbert 22 210
Hilbert basis theorem 2.20ff
Hilbert division ring 2.0f
Hilbert Fourteenth problem 2.21Bf
Hilbert group ring 11.14
Hilbert Problem (= HP) 2.21Bf
Hilbert ring 3.36s
Hilbert Seventeenth Problem, Part II see "Artin E."
Hilbert — Nullstellensatz 2.30C 3.36B
Hilbert — Syzygy theorem 14.9
Hilbert, David 267 271 308 315 315n
Hildebrandt, T.H. 291
Hill, George William 300
Hille, Einar 313
Hingley, Ronald 303
Hinohara 109 123
Hinohara theorem 3.23C 6.3Af
Hirano — Park theorem 8.4F
Hitler, Adolph 269—272 274 274n
Hochschild 24 49 99
Hochschild theorem 4.15B 14.15.4
Hochschild, Gerhard 291 301
Hochster 174
Hochster — Murthy theorem 10.1
Hocking, John G. 261
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



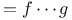 ) module
) module  ) module
) module