|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faith C. — Rings and Things and a Fine Array of Twentieth Century Associative Algebra |
|
|
 |
| Предметный указатель |
Vamos — Faith 5.19
Vamos — Menal theorem 6.22—6.23
Vamos, Peter 308—310
Van der Waerden 9 11—12 37 39 41 49 255
Vandermeer, Johnny 303n
Vanishing ideal 3.31
Vanishing radical 3.31
Vanishing, left 3.31 3.80
Varadarajan 8
Variety, algebraic 2.30As
Variety, irreducible 2.30As
Vasconcelos 81 134 198
Vasconcelos conjecture 13.23
Vasconcelos theorem 5.23A 5.24 12.9 14.20
Vasconcelos, Wolmer 319n
Vasershtein 123
Vasershtein, Boris 309
Veblen, Oswald 284
Vicknair 111
Vila 35—36
Villamayor 60 148
Villamayor ring 3.19A
Villamayor theorem 3.19A 7.38s
Vinsonhaler theorem 3.5F
Viola-Prioli 190
Viola-Prioli theorem 12.12
Viswanathan 230
VNR see "von Neumann"
VNR ring 4.As
von Goethe, Johann Wolfgang 265
von Neumann 89 179 187
von Neumann coordinization theorem 12.4
von Neumann dimension function 12.4f
von Neumann regular (= VNR) ring 4.As
von Neumann regular ring 4.Ass
von Neumann, John ("Johnny") 280—281 291 303
Voss 78
Wadsworth 169
Wagner 48
Wagner identity 15.1(4)
Wagner theorem 2.50f
Waksman 297
Waldheimer 274n
Walker, C.L. 184
Walker, Carol 281—282 306—307
Walker, E.A. 110 184
Walker, Elbert A. 281—282 306—307
Walker, G.L. see "Perlis"
Walker, Gordon L. 260
Walker, R.J. 260
Wang 35
Ward, James A. 255
Warfield 121—122 160 see
Warfield theorem 3.57 5.3C—5.3D 6.D 6.5A—6.5B 6.46 7.5C—7.5D 8.H 8.2B 8.4A 8.4D 8.4H 8.8
Warfield — Goodearl theorem 6.3H 8.4H
Warfield, Robert 309
WARNING 23 101
Wasan, Kamlesh 292
Weak 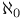 injective 4.2Bs injective 4.2Bs
Webber 143
Webber theorem 7.1
Wedderburn 21 23—24 27 57 78
Wedderburn factor 2.52ff
Wedderburn theorem on finite division rings 2.6ff
Wedderburn theorems §2
Wedderburn — Artin theorem 2.1—2.4
Wedderburn, J.H.M. 315 319
Wehlen 49
Weibel, Charles ("Chuck") 304—305
Weil, Andre 278
Weiss, Marie 255
Weyl algebra 7.19s 14.15 14.46
Weyl, Herman 285
Whitcomb 176—177
| Whitney, Gertrude 292
Whitney, Hassler ("Hass") 268—269
Wiegand theorem 5.7—5.8 5.24—5.25
Wiegand, R. 114 154
Wiegand, R. problem 5.26
Wiegand, Roger 309
Wiegand, Sylvia 309
Wielandt 71
Wilder, Billy 265
Wiles, Andrew 301 318
Wilkerson 62
Wilson, Jay 318—319
Wilson, Robert Lee 302n
Wisbauer 64 189
Witherspoon, John 318
Witt 23
Witt, Ernest 273—274
Wolfson, Kenneth 298—300
Wolfson, Roz 300
Wong 57 93 180 232 see
Wood see "Lawrence"
Wood, Japheth 291
Woodin, H.G. 266
Woolf, Harry 278 280
Woolf, Patricia Kelsh 279—280
Wordsworth, William xxix
Wuerfel theorem 6.8—6.9
Xue 106 193—195 197
Xue theorem 6.15 9.1
Yamagata theorem 8.5
Yang, Ning Chang 278—279
Yeager, "Chuck" 261
York, Linda 258
Yoshimura 104 120 185 191
Yoshimura theorem see remark 12.14
Youngman, Henny 258n 298
Yousif 104 122
Yousif theorem 12.8
Yu 157
Yue 65
Zacharias theorem [88]
Zaks, Abraham 287
Zalesski 141
Zalesski theorem 4.6E
Zalesski — Neroslavskii theorem 7.12s
Zanardo 135 see
Zaring, Wilson 284
Zariski 85 108
Zariski theorem 1.31A
Zariski, Oscar 301
Zariski-Samuel 13 34 36—38 71
Zassenhaus 87
Zelinsky 4 24 49 108 161 163 194 207
Zelinsky theorem 2.16G 8.B
Zelinsky — Sandomierski theorem 13.3
Zelmanowitz 36 130—131 180 193 236
Zelmanowitz theorem §12
Zeno, of Citrium 296n
Zeno, of Elea 296n
Zero divisors of a module 16.11
Zero divisors question 11.12s
Zero divisors, few 9.9s
Ziegler theorem 6.49
Zig-zag theorem 6.25
Zimmerman 189
Zimmermann theorem 1.25 6.D' 6.55 11.8
Zimmermann — Huisgen theorem 6.56
Zimmermann-Huisgen 68 189
Zip McCoy rings 6.38f
Zip rings 6.32s 6.38 6.39 16.28B
Zippin, Leo 267
Zjabko 30
Zjabko theorem 2.16JF
Zorn Lemma 2.17A
Zuckerman, G.M. 297
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



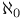 injective
injective