|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Faith C. — Rings and Things and a Fine Array of Twentieth Century Associative Algebra |
|
|
 |
| Предметный указатель |
Pappus 23
Paravaluation 9.11f
Pardo see “Gomez”
Park 94
Park theorem 8.4F
Parshall 23
Parshall, Karen H. 258
Pascaud 101
Passman 46 96 176 177—178 227 254
Pedoe, A. 291
Pendleton 231
Pendleton — Ohm theorem 14.36
Penrose, Sir Roger 323—324
Perello, Carlos 308
Perfect ring 3.31s
Perils radical 3.33Cf
Perils — Jacobson radical 3.33Cf
Perils — Walker theorem 11.11
Perlis 70 243
Perlis — Jacobson radical 3.33Cf
Perlis, Sam 256—259 260
PF ring 4.20
Piatetski-Shapiro 291
Picasso, Pablo 271 311n
Pickel see "Hartley"
PID 1.15s
Pierce 216
Pillay 62 104 111 117—118
Pillay theorem 3.6A—3.6E 4.1B
Pillay, Kanyakumari 305
Pillay, Khandon 305
Pillay, Lalita 305
Pillay, Poobhalan ("Poo") 285 305—306 309
Poincare, Henri 300 317
Polynomial identity (PI) ring 15.1s 15.14s
Pomerance, C. 290n
Popescu 70 171—172
Popescu theorem 3.33D 9.36s
Posner 227
Posner theorem 15.6
Power series ring  (also R[[x]]) 2.0s 6.12ff (also R[[x]]) 2.0s 6.12ff
Primary decomposable 5.1A'
Primary ideal 2.25
Primary ring 5.1A's
Prime avoidance 16.5ff (Cf.
Prime ideal 2.18As 2.22s
Prime radical 2.31f
Prime ring 2.22s
Prime, associated 2.25 16.11
Prime, Noetherian 16.9Ds
Prime, rank of a 2.22s
Prime-avoidance theorem 16.5 16.7A—16.7B 16.8A
Primitive ideal 2.6s
Primitive ring 2.6s
Principal ideal domain (PID) 1.14ff 1.15s
Principal ideal ring (PIR) 5.1Bs
Principal ideal theorem 2.22
Principal indecomposable module (= prindec) 3.30f
Prindec see "Principal indecomposable"
Procesi 72 99
Product theorem 5.28
Projective cover 3.30s 3.31
Projective geometry 4.Ass
Projective module 3.1As
Projective, uniformly big 3.26
Proper polynomial identity 15.4s
Proust, Marcel 283
Pruefer domain 4.1D 9.29s
Pruefer ring 9.29s
Pruefer, discrete 9.35f
Pruefer, strong 9.35s
Pseudo-Frobenius (PF) ring 4.20
Pseudo-Frobenius ring 4.20
Pseudo-injective module 6.36As
Puninski 64
Puninski theorem 6.E
Pure essential extensions 6.46 6.46A
Pure injective module 1.25 6.Bs 6.45 6.45ff
Pure-injective envelope 6.46
Pure-injective module 1.25s 6.Af
Pure-quotient infective 6.46(AB)
Pure-semisimple module 6.56s
Purely infinite ring 4.8s
Purely inseparable extension 2.9Af
Pusat — Yilmaz — Smith theorem 14.38
q.f.d. see "Quotient finite dimensional"
Qf see "Quasi-Frobenius"
QF-1 rings 13.29s 13.30 13.30E
Quasi-Frobenius (QF) ring 3.5Bs
Quasi-Frobenius extension 13.27
Quasi-Frobenius ring 3.5Af 4.23B §13
Quasi-injective hull 3.9D
Quasi-injective module 3.9As
Quasi-valuation 9.10s
Quasiregular element 3.33Cf
Quasiregular ideal 3.33Cf
Quentel theorem 9.24(5)
Quigley theorem 1.33—1.34
Quillen — Suslin theorem 3.25
Quotient see "Martindale" "Ore"
Quotient CS 12.4Cs
Quotient finite dimensional module 3.13s 5.20As 7.27—7.31
Quotient finite dimensional ring 3.13s
Quotient ring 3.12Bf
Radical extension of a ring 2.9s 2.10s
Radical of a module 3.19As
Radical of a ring 2.6s
Radical, Baer 2.38A
Radical, ideal 2.22s
Radical, Jacobson 2.6s
Radical, Koethe 3.50s
Radical, lower nil 2.38A
Radical, nil 2.34s
Radical, Perlis 3.33Cf
Radical, prime 2.31f
Radical, T-nilpotent 3.31
Radical, vanishing 3.31
Ramamurthi — Rangaswamy theorem 6.16
Ramanathan, K.G. 294
Ramanujan (Prize) 282
Ramras — Snider theorem 14.23
Rank of a free module 1.1
Rank of a prime ideal 2.22s
Rao 99
Rao, Ranga 292
Raphael, Robert 309
Rational extension of a module 12.0Ass
Rational extension, maximal 12.0Ass
Rationally complete module 12.0B
Ratliff 168
Raynaud 210
Razmyslov 227
RD-pure submodule 1.17As
Reagan, Ronald ("Ron") 272
Reduced group 1.11
Reduced order of a group of automorphisms 2.7s
Reduced part of a group 1.12
Reduced rank of a ring 3.56s
Reduced ring §12
Reeves, Billy 322
Refinement of chains of submodules 2.17F
Refinement Theorem 2.17F
Regev theorem 15.13
Regis, Ed 281 316
Regular element 2.16Fs 3.6As 3.12Bf 3.55
Regular local ring 14.16s
Regular, strongly 4.3As 4.19As
Regular, top 12.5s
Reichardt theorem 2.21Bf
Reiner 18 103 219
| Reis 230
Reis — Viswanathan theorem 16.As 16.8Af
Reisel 49
Reiten 161 see
Rentschler 211 218
Rentschler — Gabriel theorem 14.28A
Rentschler, Rudolph 277
Representations of bounded degree 15.1(7) 15.12 15.17ff
Resco 22 66 197
Resco — Stafford — Warfield theorem 3.36E
Resco, Richard 287
Restricted maximal condition 7.38s
Restricted minimum condition 7.38s
Restricted right minimum condition (= RRM) 7.38S
Restricted right socle condition (= RRS) 7.38s
Ribenboim 18 127 176
Richman theorem 9.29B 12.3
Richmond, Ered 306
Richoux 30
Rief, Rita 314
Rieffel 77
Rieffel, Marc 319—320
Rim 254
Rinehart 143
Rinehart theorem 14.15.8
Rinehart, George 303n
Riney, David 261
Ring minus-1 1.1
Ring, aleph (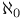 )-continuous 12.4As )-continuous 12.4As
Ring, almost maximal valuation 5.4Bs
Ring, arithmetical 6.4 6.5A
Ring, Artinian 2.1f
Ring, balanced 13.29s
Ring, basic 3.52
Ring, boolean 2.17E
Ring, bounded 5.44Bs
Ring, Camillo 3.33' 5.20
Ring, chain 3.14As
Ring, co-Noetherian 7.49
Ring, cogenerator 3.3'(4) 3.5B' 4.20ff
Ring, conch 9.10s
Ring, continuous 12.4As
Ring, Dedekind Finite (DF) 4.6A 4.6.A'
Ring, Dedekind Infinite 4.6B
Ring, endomorphism 1.2
Ring, F-semiperfect 6.52s
Ring, FBM 8.8ff 11.11ff
Ring, FFM 8.8ff 11.11ff
Ring, finite module type 8.8ff
Ring, finite representation type see "FFM"
Ring, FPF 4.26s see
Ring, generalized Boolean 2.8B
Ring, generalized uniserial (serial) 5.1Bs
Ring, Goldie 3.13s
Ring, Hilbert 3.36s
Ring, injective cogenerator 3.3'(4) 3.5' 4.20ff
Ring, Krull 9.21s
Ring, lift/rad 3.30f
Ring, linearly compact 5.4Af
Ring, local 3.14f
Ring, Loewy 3.33As
Ring, Manis 9.10s
Ring, Marot 9.20s
Ring, matrix §2 2.16Dff
Ring, matrix cancellable §10 p.174
Ring, max 3.31 3.32ff
Ring, maximal 5.4Aff
Ring, Noetherian 2.1f
Ring, nonsingular 4.2s 5.3Ds §12
Ring, opposite 2.5Bf 2.43s
Ring, Osofsky 3.33'
Ring, perfect 3.31s
Ring, PF 4.20
Ring, PP (= PP) 7.3As
Ring, primary 5.1A's
Ring, primary-decomposable 5.1A'
Ring, prime 2.22s
Ring, primitive 2.5s
Ring, product 1.3
Ring, pseudo-Frobenius (PF) 4.20
Ring, q.f.d. 5.20As 7.27—7.31
Ring, QF-1 13.29s
Ring, QI 3.9A 7.37f 7.39—7.43
Ring, quasi-Frobenius (QF) 3.5Af 4.23B §12
Ring, radical extension 2.10s
Ring, radical of a 2.6s 3.33Cf
Ring, reduced §12
Ring, regular local §15
Ring, S 12.0As see
Ring, sandwich 9.14s
Ring, SBI 3.54f 8.4Bs
Ring, self-injective 3.2s 3.5Af 4.5ff 4.20ff 5.42 6.28
Ring, semiartinian 3.33As
Ring, semilocal 3.11As
Ring, semiperfect 3.30s 6.52s
Ring, semiprimary 3.11As 5.1A's
Ring, semiprime 2.2s 2.34
Ring, semiprimitive 2.6f
Ring, semisimple 2.1
Ring, serial 5.1Bs
Ring, sigma cyclic 5.1s
Ring, similar 3.51f
Ring, simple 2.1f
Ring, skalar 12.0As
Ring, stable range of a 6.3Fs
Ring, subdirect product of 2.6ff
Ring, subdirectly irreducible 2.17D
Ring, triangular matrix 2.6s
Ring, uniserial 5.1Bs
Ring, valuation 3.14As 5.1A'f
Ringdal see "Amdal"
Ringel 160 254
Ringel theorem 13.30E
Ringel, Klaus 287
Ritt 143
Ritt (Lecturer) 287
Ritt algebra 7.16s
Ritter 88
Rizvi 150 188
Rizvi theorem 12.4D 12.7
Rizvi — Yousif theorem 12.4D 12.8
Robertson, Malcolm 291
Robinson 129
Robson 74 80 181 211
Robson theorem 7.4
Rockefeller (Institute) 278
Roggenkamp 177
Roggenkamp theorem 11.11f
Roiter 160
Roitman 164
Roitman theorem 9.3 9.8
Roitman — Scott theorem 11.10ss
Roos 143 209
Rose — Baldwin theorem 3.43As
Roseblade theorem 11.12 11.14
Roselli 194
Rosenberg 4 24 49 161 207
Rosenberg theorem 2.16J
Rosenberg — Rinehart theorem 14.15.11
Rosenberg, Alex 303n
Rosenthal, Arthur 255
Rothenberger, Fritz 291—292
Rowen 44—45 76 224
Rowen PI-algebra 15.14s
Rowen polynomial 15.14s
Royster, Kimberly 255
Rubin 190
Rubin theorem 12.11
Rubin, Jerry 321
Russell, Bertram 323
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 (also R[[x]])
(also R[[x]]) 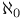 )-continuous
)-continuous