|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Knuth D.E. Ч The art of computer programming (vol. 2 Seminumerical Algorithms) |
|
|
 |
| ѕредметный указатель |
Divided differences 504 516
Dividend: the quantity u while computing [u/v] and u mod v 270
Division 194 265 270Ч275 278 282Ч284 311Ч313
Division, algebraic numbers 333 674
Division, avoiding 523Ч524
Division, balanced ternary 283
Division, by ten 321 328
Division, by zero 220 224 241 639
Division, complex 228 283 706
Division, continued fractions 649
Division, double-precision 251Ч252 278Ч279
Division, exact 284
division, floating point 220Ч221 230Ч231 243
Division, fractions 330
Division, long 270Ч275 278 282Ч284
Division, mixed-radix 209 635
Division, mod m 354 445 499
Division, multiprecision 270Ч275 278Ч279 282Ч283 311Ч313
Division, multiprecision by single-precision 282
Division, polynomial 420Ч439 487 534
Division, power series 525Ч526 533Ч534
Division, pseudo- 425Ч426 435Ч436
Division, quater-imaginary 283
Division, short 282
Division, string polynomials 436Ч437
Divisor (x is a divisor of y if y mod x = 0 and x > 0; it is a proper divisor if it is a divisor such that 1 < x < y), polynomial 422
Divisor: The quantity v while computing [u/v] and u mod v 270
Dixon, John Douglas 372 401Ч402 412 414 415 417
Dixon, Wilfrid Joseph 565
Dobell, Alan Rodney 17
Dobkin, David Paul 697 712
Dodgson, Charles Lutwidge 435
Donsker, Monroe David 559
Doob, Joseph Leo 559
Dorn, William Schroeder 488
Dot product 36 97 173Ч174 499Ч501
Double-precision arithmetic 246Ч253 278Ч279 295
Doubling 322 462
Doubling step 467
Doubling, continued fraction 375
Downey, Peter James 485
Dragon curve 606 609 655
Dragon sequence 655
Dresden, Arnold 196
Drift 237 244
Du Shiran 287
Dual of an addition chain 481 484
Duality formula 569
Duality principle 481 485 507 535 718
Dubner, Harvey Allen 664
Dumas, Philippe 355
Duncan, Robert Lee 264
Duodecimal number system 199Ч200
Dupre, Athanase 653
Durbin, James 57 568
Durham, Stephen Daniel 34
Durstenfeld, Richard 145
e 12 76 359 726Ч727 733
Earle, John Goodell 312
Eckhardt, R. 189
Edelman, Alan Stuart 280
Edinburgh rainfall 74
EDVAC computer 225Ч226
Effective algorithms 161Ч166 169 178
Effective information 179
Egyptian mathematics 335 462
Eichenauer-Herrman, Jiirgen 32 558 559
Eisenstein, Ferdinand Gotthold Max 457
Electrologica X8 computer 222
Electronic mail 406
Elementary symmetric functions 682Ч683
Elkies, Noam David xi
Ellipsoid 105
Ellipsoid, random point on 141
Elliptic curve method 402
Empirical distribution functions 49
Empirical tests for randomness 41 61Ч80
Encoding a permutation 65Ч66 77Ч78 145
Encoding secret messages 193 403Ч407 415 417
Enflo, Per 683
Engineering Research Associates 208
Enhancing randomness 26 34
ENIAC computer 54 280
entropy 712
Enumerating binary trees 527 696 723
Enumerating prime numbers 382 412 416
Equality, approximate 224 233Ч235 239 242Ч243 245
Equidistributed sequence 150 163 177 179Ч183
Equidistribution test 61 74 75
Equitable distribution 181
Equivalent addition chains 480 484
Eratosthenes of Cyrene 412
Erdos, Pal (= Paul) 181 384 471 696
ERH see УExtended Riemann hypothesisФ
ERNIE 3
Error estimation 222 229 232 253 255 309Ч310
Error, absolute 240 309 312Ч313
Error, relative 222 229 232 253 255
Espelid, Terje Oskar 616
Essential 233Ч235 239Ч240 242Ч244
Essential equality 233Ч235 239Ч240 242Ч244
Estes, Dennis Ray 671
Estrin, Gerald 488
Euclid 335Ч337
Euclid's Algorithm 86 99 102 117 184 288 304 334Ч337 340 579
Euclid's algorithm, analysis of 356Ч379
Euclid's algorithm, compared to binary algorithm 341
Euclid's algorithm, extended 342Ч343 354 379 435Ч436 534
Euclid's algorithm, for polynomials 424 438Ч439Ч
Euclid's algorithm, for polynomials, extended 437 458
Euclid's algorithm, for string polynomials 426Ч428
Euclid's algorithm, generalized to the hilt 426Ч428
Euclid's algorithm, multiprecision 345Ч348 373
Euclid's algorithm, original form 335Ч336
Eudoxus of Cnidus 335 359
Euler, constant  359 379 726Ч727 733 359 379 726Ч727 733
Euler, Leonhard (Ёйлер, Ћеонард) xi 357 375 377 392 407 526 649Ч651 653 655
Euler, theorem 20 286 548
Euler, totient function 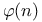 19Ч20 289 369 376 583 646 19Ч20 289 369 376 583 646
Eulerian numbers 284
Evaluation (computing the value), of determinants 498Ч500 523Ч524
Evaluation (computing the value), of mean and standard deviation 232 244
Evaluation (computing the value), of monomials 485 697
Evaluation (computing the value), of polynomials 485Ч524
Evaluation (computing the value), of powers 461Ч485
Eve, James 493 517
Eventually periodic sequence 7 22 375 385
Exact division 439
Excess q exponent 214Ч215 227 246
Exclusive OR 31 32 193 419
Exercises, notes on ixЧxi
Exhaustive search 103
Exponent overflow 217 221 227 231 241 243 249
Exponent part of a floating point number 214Ч215 246 263 283
Exponent underflow 217 221Ч222 227 231 241 249
Exponential deviates, generating 132Ч133 137
Exponential distribution 133 137 589
Exponential function 313 490 533 537
Exponential sums 84Ч85 110Ч115 181 305 382 501
Exponentiation (raising to a power) 461Ч485
Exponentiation (raising to a power) multiprecision 463
Exponentiation (raising to a power) of polynomials 463Ч464
Exponentiation (raising to a power) of power series 526 537 719Ч
Extended arithmetic 244Ч245 639
Extended Euclidean algorithm 342Ч343 354 379 435Ч436 534
Extended Euclidean algorithm, for polynomials 437 458
Extended Riemann hypothesis 395Ч396 671
F-distribution 135
Factor method of exponentiation 463 465 482 485
Factorial number system 66 209
| Factorial powers 297 515 534 643 731
Factorials 416 622
Factorization (discovering factors), of integers 13Ч14 175 379Ч394 396Ч403 412Ч417
Factorization (discovering factors), of polynomials 439Ч461 514
Factorization (discovering factors), of polynomials mod p 439Ч449 455Ч456
Factorization (discovering factors), of polynomials over the integers 449Ч453
Factorization (discovering factors), of polynomials over the rationals 459
Factorization (discovering factors), optimistic estimates of running time 176
Factorization (discovering factors), uniqueness of 436
FADD (floating add) 223Ч224 227Ч228 238 253 516
Fagin, Barry Steven 403 632
Falling powers 297 731
Fan, Chung Teh 143
Fast Fourier Transform 73 306Ч310 318 502 505 512 516 706 710 713Ч714
Fast Fourier transform, history of 701
Fateman, Richard J. 463
Faure, Henri 164
FCMP (floating compare) 223 244
FDIV (floating divide) 223
Feijen, Wilhelmus [= Wim] Hendricus Johannes 636
Ferguson, Donald Fraser 280
Ferranti Mark I computer 3 192
Ferrenberg, Alan Milton 189
FFT 516 (see УFast Fourier transformФ)
Fibonacci, generator 27 34 36 37 47 52 54 92
Fibonacci, Leonardo, of Pisa 197 208 280
Fibonacci, number system 209
Fibonacci, numbers 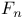 : elements of the Fibonacci sequence 731 : elements of the Fibonacci sequence 731
Fibonacci, numbers, table of 728
Fibonacci, sequence 27 37 213 264 360 468 660 666
Fibonacci, sequence, lagged 27Ч29 35 40 72 75 79Ч80 146 186Ч188 193
Field (an algebraic system admitting addition, subtraction, multiplication, and division) 213 331 420 422 506 525
Field (an algebraic system admitting addition, subtraction, multiplication, and division), finite 29Ч30 449 457 554Ч555 702
Fike, Charles Theodore 490
Finck, Pierre Joseph Etienne 360
Finite fields 29Ч30 449 457 554Ч555 702
Finite Fourier transform see УDiscrete Fourier transformФ
Finite sequences, random 167Ч170 178
Fischer, Michael John 634
Fischer, Patrick Carl 241
Fischlin, Roger 669
Fisher, Ronald Aylmer 145
Fishman, George Samuel 108
FIX (convert to fixed point) 224
Fix-to-float conversion 221 223Ч224
Fixed point arithmetic 214 225Ч226 308Ч310 532
Fixed slash arithmetic 331Ч333 379Ч
Flajolet, Philippe Patrick 355 366 449 541 644
Flammenkamp, Achim 478 483 693
Flat distribution see УUniform distributionФ
Flehinger, Betty Jeanne 262
Float-to-fix conversion 224Ч225 228
Floating binary numbers 214 225 227 254 263
Floating decimal numbers 214 226 254Ч264
Floating hexadecimal numbers 254 263
Floating point arithmetic 36 188 193 196 214Ч264 292
Floating point arithmetic, accuracy of 222 229Ч245 253 329 438 485
Floating point arithmetic, addition 215Ч220 227Ч228 230Ч231 235Ч238 253Ч254 602
Floating point arithmetic, addition, exact 236
Floating point arithmetic, axioms 230Ч231 242Ч245
Floating point arithmetic, comparison 233Ч235 239 242Ч243
Floating point arithmetic, decuple-precision 283
Floating point arithmetic, division 220Ч221 230Ч231 243
Floating point arithmetic, double-precision 246Ч253 278Ч279
Floating point arithmetic, hardware 223Ч226
Floating point arithmetic, intervals 228 240Ч242 244Ч245 333 613
Floating point arithmetic, mod 228 243 244
Floating point arithmetic, multiplication 220 230Ч231 243 263Ч264
Floating point arithmetic, multiplication, exact 244
Floating point arithmetic, operators of MIX 215 223Ч225 516
Floating point arithmetic, quadruple-precision 253
Floating point arithmetic, reciprocal 243 245 263
Floating point arithmetic, single-precision 214Ч228
Floating point arithmetic, subtraction 216 230Ч231 235Ч238 245 253 556 602
Floating point arithmetic, summation 232 244
Floating point arithmetic, triple-precision 252
Floating point arithmetic, unnormalized 238Ч240 244 327
Floating point numbers 196 214Ч215 222 228 246
Floating point numbers, radix-b, excess-g 214Ч215
Floating point numbers, statistical distribution 253Ч264
Floating point numbers, two's complement 228
Floating point radix conversion 326Ч329
Floating point trigonometric subroutines 245 247 490
Floating slash arithmetic 331 333
Floor function [x] 81 732
FLOT (convert to floating point) 223
Floyd, Robert W. 7 148 280 361 505 540
FMUL (floating multiply) 223 516
Foata, Dominique Cyprien 9
Forsythe, George Elmer 4 128
FORTRAN language 188 193 279 600 602
Fourier, division method 278
Fourier, Jean Baptiste Joseph 278
Fourier, series 90 487
Fourier, transform, discrete 169 305Ч311 316Ч318 501Ч503 506 512 520Ч521 524 595 700
Fractals 206
Fraction overflow 217 254 262 264
Fraction part of a floating point number 214Ч215 246 263
Fraction part of a floating point number, distribution of 254Ч264
Fractions, conversion 319Ч328
Fractions, decimal, history 197Ч198 326
Fractions, exponentiation 483
Fractions, random see УUniform deviatesФ
Fractions, terminating 328
Fractions: numbers in [0..1) 36
Fractions: rational numbers 330Ч333 420 526
Fraenkel, Aviezri S. 290 291 292 630
Franel, Jerome 258
Franklin, Joel Nick 149 158 159 177 180 182 577
Franta, William Ray 60
Fredricksen, Harold Marvin 557
Free associative algebra 437
Frequency function see УDensity functionФ
Frequency test 61 74 75
Friedland, Paul 613
Frieze, Alan Michael 599
Frobenius, automorphism 689
Frobenius, Ferdinand Georg 681 689
Frye, Roger Edward 538
FSUB (floating subtract) 223 253
Fuchs, Aime 9
Fundamental Theorem of Arithmetic 334 422 483
Gage, Paul Vincent 409
Galambos, Janos 661
Galois, Evariste 449 457
Galois, fields see УFinite fieldsФ
Galois, groups 679 681 689 690
Gambling systems 161
Gamma distribution 133Ч134 140
Gamma function, incomplete 56 59 133
Ganz, Jurg Werner 707
Gap test 62Ч63 74Ч76 136 158 180
Gardner, Martin 41 200 280 592
Garner, Harvey Louis 280 290 292
Gauss, Johann Friedrich Carl (= Carl Friedrich) 20 101 363 417 422 449 578 679 685 688 701
Gauss, lemma about polynomials 422Ч423 682
Gaussian integers 292 345 579
Gay, John 1
Gebhardt, Friedrich 34
Gehrhardt, Karl Immanuel 200
Geiger, Hans, counter 7
Geiringer, Hilda, von Mises 76
Generalized Dedekind sums 83Ч92 106
Generalized Riemann hypothesis 396
Generating functions 140 147 213 261 276Ч278 525 562Ч563 679Ч680 686 695
Generation of uniform deviates 10Ч40 184Ч189 193
Genuys, Francois 280
Geometric distribution 136 137 140 585
Geometric mean 283
Geometric series 84 307 519 700
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




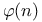
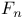 : elements of the Fibonacci sequence
: elements of the Fibonacci sequence