|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Knuth D.E. Ч The art of computer programming (vol. 2 Seminumerical Algorithms) |
|
|
 |
| ѕредметный указатель |
Power series: a sum of the form  see УGenerating functionsФ see УGenerating functionsФ
Power tree 464 481
Poweroids 534Ч536 722
Powers, Don M. 312
Powers, evaluation of 461Ч485
Powers, evaluation of, multiprecision 463
Powers, evaluation of, polynomial 463Ч464
Powers, evaluation of, power series 526 537 719
Powers, Ralph Earnest 396 407
pp: primitive part 423Ч425
Pr: probability 150 152 168 179Ч180 257 264 472 734
Pratt, Vaughan Ronald 356 413
Precision (the number of digits in a representation), double 246Ч253 278Ч279 295
Precision (the number of digits in a representation), multiple 58 202 265Ч318 419 486
Precision (the number of digits in a representation), quadruple 253 295
Precision (the number of digits in a representation), single: fitting in one computer word 215
Precision (the number of digits in a representation), unlimited 279 283 331 416
Preconditioning see УAdaptationФ
Prediction tests 171 183
Preston, Richard McCann 280
Primality testing 380 391Ч396 409Ч414 549
Prime chains 415 666
Prime numbers, distribution of 381Ч382 405
Prime numbers, enumeration of 381Ч382 416
Prime numbers, factorization into 334
Prime numbers, largest known 407Ч412
Prime numbers, Mersenne 185 409 412 413
Prime numbers, size of mth 665
Prime numbers, useful 291 405 407Ч408 549Ч550 711
Prime numbers, useless 415
Prime numbers, verifying primality of 380 391Ч396 409Ч414 549
Prime numbers: integers greater than unity having no proper divisors 380
Primes in a unique factorization domain 421Ч422
Primitive element modulo m 20Ч23
Primitive notations for numbers 195 198
Primitive part of a polynomial 423Ч425
Primitive polynomial 422 436
Primitive polynomial modulo p 30Ч32 422
Primitive recursive function 166
Primitive root: A primitive element in a finite field 20Ч23 185 391 417 456 457
Pritchard, Paul Andrew 631
Probabilistic algorithms see УRandomized algorithmsФ
Probability, abuse of 433
Probability, over the integers 150 152 257 264 472
Probability: ratio of occurrence 150 177 257
Probert, Robert Lorne 699
Programming languages 16 185 222
Pronouncing hexadecimal numbers 201
Proof of algorithms 281Ч282 336Ч337 592
Proofs, constructive versus nonconstructive 286 289 583 630
Proth, Francois Toussaint 663
Proulx, Rene 179
Pseudo-division of polynomials 425Ч426 435Ч436
Pseudorandom sequences 4 170Ч176 179
Ptolemy, Claudius 197
Public key cryptography 406
Purdom, Paul Walton, Jr. 541
Pyke, Ronald 566
q-series 536
Quadratic congruences, solving 417
Quadratic congruential sequences 26Ч27 37
Quadratic forms 98 521
Quadratic forms, minimizing, over the integers 98Ч101 105 115Ч118
Quadratic irrationalities, continued fractions for 358 374Ч375 397Ч401 412 415 665
Quadratic reciprocity law 393 411 414 663
Quadratic residues 415 697
Quadratic sieve method 402
Quadruple-precision arithmetic 253 295
Quandalle, Philippe 710
Quasirandom numbers 4 189
Quater-imaginary number system 205 209Ч210 283
Quaternary number system 195 200
Quick, Jonathan Horatio 77 147
Quinary number system 195 200 213
Quolynomial chains 498 524 704
Quotient, of polynomials 420Ч421 425Ч426 534
Quotient, partial 87 106 117 346 359 362Ч369 379 656 665
Quotient, trial 270Ч272 278 282
Quotient: [u/v] 265 (see УDivisionФ)
Rabin, Michael Oser 175 396 406 413 415 448 449 707
Rabinowitz, Philip 279
Rademacher, Hans 90 91
Radioactive decay 7 132 137
Radix conversion 200 204 205 207 210 319Ч329 486 489
Radix conversion, floating point 326Ч329
Radix conversion, multiprecision 326 328
Radix point 10 185 195 204 209 214 319
Radix, complex 205Ч206 209Ч210
Radix, irrational 209
Radix, mixed 66 199 208Ч211 290 293 505
Radix, negative 204Ч205 209Ч210 212 328
Radix: base of positional notation 195
Rail, Louis Baker 240 242
Raimi, Ralph Alexis 257 262
Raleigh, Walter 199
Ramage, John Gerow 135
Ramanujan Iyengar, Srinivasa 662
Ramaswami, Vammi 383
Ramshaw, Lyle Harold 164 181
ran-array 186Ч188 193
Rand Corporation 3
Randell, Brian 202 225
Random bits 12 30Ч32 35Ч36 38 48 119Ч120 170Ч176
Random combinations 142Ч148
Random directions 135Ч136
Random fractions 10 (see УUniform deviatesФ)
Random functions 4Ч9 385
Random integers, among all positive integers 257 264 342 354
Random integers, in a bounded set 119Ч121 138 185Ч186
Random mappings 4Ч9 385 657Ч658
Random number generators 1Ч193
Random number generators, for nonuniform deviates 119Ч148
Random number generators, for uniform deviates 10Ч40 184Ч189 193
Random number generators, machines 3 404
Random number generators, summary 184Ч193
Random number generators, tables 3
Random number generators, testing 41Ч118
Random number generators, using 1Ч2 119Ч148 664
Random permutations 145Ч148 384 460 679
Random permutations, of a random combination 148
Random point, in a circle 123
Random point, in a sphere 136
Random point, on a sphere 135
Random point, on an ellipsoid 141
Random polynomials 435 448 455 459
Random random number generators 6Ч9 26
Random real numbers 255 263
Random samples 142Ч148
Random sequences, finite 167Ч176 178Ч179 183
Random sequences, meaning of 2 149Ч183
Randomized algorithms: algorithms that use random numbers and usually produce a correct answer 1Ч2 171 395Ч396 401Ч402 413Ч417 436 447Ч449 453 459 669 688
Randomness, guaranteed 35Ч36 170Ч176
RANDU 26 107 188 551
Rangan see УPandu RanganФ
Range arithmetic 228 240Ч242 244Ч245 333 613
Rank, of apparition 410Ч411
Rank, of apparition, of a matrix 443Ч444 506 508 520
Rank, of apparition, of a tensor 506 508 514 520Ч524
RANLUX 109
Rap music 3
Rapoport, Anatol 541
Ratio method 130Ч132 133 140
Rational arithmetic 69 330Ч333 427Ч428 526
Rational function approximation 438Ч439 534
Rational functions 420 498 518
Rational functions, approximation and interpolation 438Ч439 505 534
Rational numbers 330 420 459
Rational numbers, approximation by 331Ч332 378Ч379 617
Rational numbers, mod m 379
Rational numbers, polynomials over 428 459
| Rational numbers, positional representation of 16 211 213 328
Rational reconstruction 379
Real numbers 420
Real Time 286
Realization of a tensor 507
Reciprocal differences 505
Reciprocals 278Ч279 312Ч313 421
Reciprocals, floating point 243 245 263
Reciprocals, mod 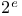 213 213
Reciprocals, mod m 26 213 354 445 456 646
Reciprocals, power series 537
Reciprocity laws 84 90 393 414
Recorde, Robert xi 280Ч281
Rectangle-wedge-tail method 123Ч128 139
Rectangular distribution see УUniform distributionФ
Recurrence relations 10 26Ч33 37Ч40 260Ч261 295 301Ч302; 318 351 362 386 409Ч411 442 525 634 687 695 714
Recursive processes 253 295 299Ч303 318 419 500 531 689 713
Reeds, James Alexander III 599
Rees, David 39 169
Registers 491
Regular continued fractions 346 358Ч359 368 374Ч379 412 415 665
Reiser, John Fredrick 28 39 242
Reitwiesner, George Walter 213 280 280
Rejection method 125Ч126 128Ч129 134 138 139 591
Relative error 222 229 232 253 255
Relatively prime, polynomials 422 436 454
Relatively prime: having no common prime factors 11 19 286 330 332 342 354
Remainder: dividend minus quotient times divisor 265 272Ч273 420Ч421 425Ч426 437 534 see
Replicative law 90
representation of 205Ч206 209Ч210 292
Representation of  225 244Ч245 332 225 244Ч245 332
Representation of numbers see УNumber systemsФ
Representation of trees 482
Reservoir sampling 143Ч144 147
Residue arithmetic 284Ч294 302Ч305 450 454 499
result set 494 517
Resultant of polynomials 433 690 674
Revah, Ludmila 706
Reverse of a polynomial 435 452 673 721
Reversing binary number system 212
Reversion of power series 527Ч530 533Ч536
Revolving binary number system 212
Rezucha, Ivan 143
Rhind papyrus 462
Rho method for factoring 384Ч386 393Ч394 413
Riccati, Jacopo Francesco, equation 650
Rieger, Georg Johann 653
Riemann, Georg Friedrich Bernhard 83 382 414
Riemann, hypothesis 382 663
Riemann, hypothesis, generalized 395Ч396 671
Riemann, integration 153Ч154 259
riffle shuffles 145 147
Ring with identity, commutative 418
Riordan, John 542
Rising powers 534 731
Ritzmann, Peter 721
Rivat, Joel 667
Rivest, Ronald Linn 403 405 707
Robber 190Ч192
Robinson, Donald Wilford 554
Robinson, Julia Bowman 666
Robinson, Raphael Mitchel 664 711
Roepstorff, Gert 366
Rolletschek, Heinrich Franz 9 345
Roman numerals 195 209
Romani, Francesco 500 715
Roof, Raymond Bradley 115
Roots of a polynomial 23 434 483 493
Roots of a polynomial, multivariate 436
Roots of unity 84 531Ч532 700 УExponential
Ross, Douglas Taylor 192
Rotenberg, Aubey 11 47
Rothe, Heinrich August 535
Rouche, Eugene, theorem 690
Roulette 2 10 55
Round to even 237 241
Round to odd 237
Rounding 102 207 217 222 223 230Ч231 236Ч237
Rounding errors 232 242 698 718
Rounding overflow 217 220 222 224 227Ч228
Rounding, mediant 331Ч332 379
Rozier, Charles P. 324
RSA box 404
RSA encryption 403Ч407 415 629 669
Rudolff, Christof 198
Rumely, Robert Scott 396
Run test 63 66Ч69 74Ч77 158 180
Runs above (or below) the mean 63
Runs in a permutation 66 74 76
Russian peasant method 462
Ruzsa, Imre Zoltan 213
Ryser, Herbert John 515 699
Saarinen, Jukka Pentti Paivio 75
Sachau, Karl Eduard 461
Saddle point method 568
Sahni, Sartaj Kumar 60
Saidan, Ahmad Salim 198 461
Salamin, Eugene 283
Salfi, Robert 145
Samelson, Klaus 241Ч242 327
Samet, Paul Alexander 321
Sampling (without replacement) 1 142Ч148
Sands, Arthur David 610
Saunders, Benjamin David 455
Savage, John Edmund 707
Sawtooth function ((x)) 81Ч82 90Ч91
Saxe, James Benjamin 141
Scarborough, James Blaine 241
Schatte, Peter 262 622
Schelling, Hermann von 65
Schmid, Larry Philip 73
Schmidt, Erhard 101 674
Schmidt, Wolfgang M 183
Schnorr, Claus-Peter 118 179 414 417 497 578 664 669
Schoenemann, Theodor 457
Schoenhage Ч Strassen algorithm 306Ч311
Schoenhage, Arnold 292 302 305 311 317 328 470 484 500 522 629 638 656 672 696 715
Scholz Ч Brauer conjecture 478 485
Scholz, Arnold 478
Schooling, William 627
Schreyer, Helmut 202
Schroeder, Friedrich Wilhelm Karl Ernst 531
Schroeder, function 531Ч532 724
Schroeppel, Richard Crabtree 399 400 671
Schubert, Friedrich Theodor von 449
Schwartz, Jacob Theodore 674 675
Schwarz (= Svarc), Stefan 442
Schwenter, Daniel 654
Secrest, Don 279 327
secret keys 193 403Ч407 415 417 505
secure communications 403Ч407 415
Sedecimal number system 202 (see УHexadecimalФ)
Sedgewick, Robert 540
Seed (starting value) 143 146 170 187Ч188 193 550 590
Seed (starting value), in a linear congruential sequence 10 17 20 184
Seidenberg, Abraham 198
Selection sampling 142Ч143 146
Selenius, Clas-Olof 648
Self-reproducing numbers 6 293Ч294 540
Selfridge, John Lewis 394 412 665
Semi-online algorithm 529
Semigroup 539
Seneschol, David 589
Septenary (radix 7) number system 200
Serial correlation coefficient 77
Serial correlation test 72Ч74 91 83 154 182
Serial test 39 60 62 74 75 78 95 106 109Ч115 158
Seroussi, Gadiel 712
Serret, Joseph Alfred 374 449 579
Sethi, Ravi 485
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте