Авторизация
Поиск по указателям
Higham N.J. — Accuracy and Stability of Numerical Algorithms
Обсудите книгу на научном форуме Нашли опечатку?
Название: Accuracy and Stability of Numerical AlgorithmsАвтор: Higham N.J. Аннотация: What is the most accurate way to sum floating point numbers? What are the advantages of IEEE arithmetic? How accurate is Gaussian elimination and what were the key breakthroughs in the development of error analysis for the method? The answers to these and many related questions are included here.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2Год издания: 2002Количество страниц: 680Добавлена в каталог: 19.06.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
GEPP see “Gaussian elimination partial Geuder, James C. 186 Ghavimi, Ali R. 315—317 Gill, Philip E. 210 226 227 229 413 476 Gill, S. 83 Givens rotation 365 Givens rotation, disjoint rotations 367—368 379 Givens rotation, fast 376 Givens, Wallace J. 29 61 Gluchowska, J. 404 GNU MP library 502 Godunov, S.K. 285 Gohberg, L. 128 129 428 Goldberg, David 35 53 85 532 Goldberg, I. Bennett 57 Goldstine, Herman H. 1 29 48 183 184 188 259 260 515 Golub, Gene H. xxviii 11 24 29 115 132 133 172 187 208 231 256 257 282 299 307 308 308 323 345 375 377 380—382 389 399 402—405 429 Goodman, R. 57 Goodnight, James H. 282 Gould, Nicholas I.M. 170 189 Govaerts, Willy J.F. 241 Gradual underflow 38 42 45 56 Gragg, W.B. 295 376 Graham, Ronald L. 79 518 Gram — Schmidt method 369—373 Gram — Schmidt method reorthogonalization 376 Gram — Schmidt method, classical 369 Gram — Schmidt method, classical, error analysis 371 373 Gram — Schmidt method, modified 370 Gram — Schmidt method, modified, connection with Householder QR factorization 353 371—372 376 Gram — Schmidt method, modified, error analysis 371—373 Gram — Schmidt method, modified, error analysis for application to LS problem 386 Gram — Schmidt method, modified, stability 24 Greenbaum, Anne 324 337 Gregory, Robert T. 29 512 522 Griewank, Andreas 469 Grimes, Roger G. 188 219 227 302 524 Grosse, Eric 573 Group inverse 331 Growth factor 165—173 Growth factor for banded matrix 173 Growth factor for block 216 218 221 226 Growth factor for complete pivoting 169—170 Growth factor for diagonally dominant matrix 172 Growth factor for partial pivoting 166—173 Growth factor for partial pivoting large growth in practical problems 167 Growth factor for random matrices 189 Growth factor for rook pivoting 170 Growth factor for tridiagonal matrix 173 Growth factor for upper Hessenberg matrix 172 Growth factor maximization by direct search 472—473 Growth factor numerical maximization for complete pivoting 170 189 Growth factor, a posteriori estimates for 180—181 Growth factor, define using exact or computed quantities 165 189 Growth factor, lower bound for 167 Growth factor, statistical model of 168 Gu, Ming 346 404 406 534 Guard digit 44 Guard digit, test for 52 Gudmundsson, Thorkell 298 Guggenheimer, Heinrich W. 284 Gulliksson, Marten 405 Gustafson, John L. 446 Gustavson, F.G. 187 Haar distribution, random orthogonal matrix from 517—518 Hadamard condition number 279 282 284 Hadamard matrix 116 168 170 193 Hadamard's inequality 284 Hager, William W. 292 301 Hall, Jr., Marshall 168 Halley's method 508 Halmos, Paul R. 511 Hamada, Hozumi 49 Hammarling, Sven J. 317 322 323 376 397 500 Hamming, R.W. 53 431 Hansen, Per Christian 133 377 448 Hanson, Richard J. 375 376 399 402 403 414 499 Harter, Richard 446 Hartfiel, D.J. 132 Harwell — Boeing sparse matrix collection 524 Hauser, John R. 57 59 Hearon, John Z. 311 Heath, Michael T. 259 388 Hedayat, A.S. 168 Hein, Piet 31 115 Helvin, Marie 153 Henderson, Harold V. 317 487 Hennessy, John L. 35 53 Henrici, Peter 48 49 61 77 344 Henson, Van Emden 456 Heron's formula 45 Heroux, Michael 446 569 Herzberger, Jiirgen 483 Hessenberg matrix Gaussian elimination 24—25 30 Hessenberg matrix, determinant of 24—25 30 280 Hessenberg matrix, growth factor for 172 Hewer, Gary 318 Hewlett — Packard HP 48G calculator condition estimator 302 Hewlett — Packard HP 48G calculator exhausting its range and precision 15—16 Hidden bit 41 Higham, Desmond J. 114 128 129 136 167 187 339 342 394 429 Higham, Nicholas J. 65 90 128 129 132 151—153 167 187 190 210 219 227 228 240—242 249—253 256 257 262 269 278 281 292 294 295 298 301—304 317 324 347 349 351 362 375 377 378 380 394—396 398 400 402—405 409 413 414 429 431 446—448 486 505 523 525 564 569 571 Hilbert matrix 512—515 523—524 Hilbert matrix determinant 513 Hilbert matrix, Cholesky factor 513 Hilbert matrix, inverse 513 Hilbert, David 523 Hildebrand, F.B. 28 35 Hodel, A. Scottedward 317 Hodges, Andrew xxix Hoelder inequality 106 107 Hoffman, A.J. 377 Hoffmann, Christoph M. 29 Hoffmann, W. 281 282 376 Hooper, Judith A. 501 Horn, Roger A. 107 115 137 152 306 342 543 547 551 554 Horner's method 94—104 Horner's method for derivatives 96—99 Horner's method for rational function 26 Horner's method running error bound 95—96 103 Horning, Jim 489 Hotelling, Harold 183 433 Hough's underflow story 506—507 Hough, David 43 506 507 Hough, Patricia D. 395 Householder transformation 354—355 Householder transformation error analysis 357—363 Householder transformation in QR factorization 355—357 Householder transformation, aggregated (WY representation) 363—365 Householder transformation, block 375 Householder transformation, choice of sign in 355 Householder transformation, history of 374—375 Householder, Alston S. 2 105 115 147 161 374 403 560 Hull, T.E. 48 50 485 503 528 Hunt, Julian 54 Huskey, H.D. 184 Hyman's method 30 280 285 Hyman, M.A. 280 IBM, ESSL library 436 438 IEEE arithmetic 39 41—43 IEEE arithmetic 42 490 492 IEEE arithmetic double rounding 43 58 IEEE arithmetic exception handling 41 491—492 IEEE arithmetic exceptions 41—42 IEEE arithmetic exploiting in software 490—493 IEEE arithmetic extended formats 42 IEEE arithmetic gradual underflow 42 IEEE arithmetic implementation using formal methods 55—56 IEEE arithmetic NaN 41—42 490 492 IEEE arithmetic parameters 371 41 IEEE arithmetic recommended auxiliary functions 492—493 IEEE arithmetic rounding modes 41 IEEE arithmetic signed zeros 42 IEEE arithmetic Standard 754 41 IEEE arithmetic Standard 854 43 IEEE arithmetic subnormal numbers 42 492 Ikebe, Yasuhiko 300 302 304 Ikramov, Khakim D. 209 525 Incertis, F. 509 Index of a matrix 331 Inertia 214 Inner product error analysis 62—65 Inner product in extended precision 64 Inner product, reducing constant in error bound 63 Intel Itanium chip 46 Intel Pentium chip, division bug 55 Internet 574 Interval analysis 41 190 481—484 Interval analysis, dependencies 482 Interval analysis, fallibility 483—484 Interval analysis, Gaussian elimination 482 Interval analysis, super-accurate inner product 483 Interval arithmetic see “Interval analysis” INTLAB 483 Inverse iteration 24 Inverse matrix 259—285 Inverse matrix bound using diagonal dominance 154 Inverse matrix in solving Ax=b stability 260 Inverse matrix left and right residuals 261 Inverse matrix perturbation theory 127—128 Inverse matrix, Csanky's method for 278 Inverse matrix, error analysis for Gauss — Jordan elimination 273—277 Inverse matrix, error analysis for LU factorization 267—271 Inverse matrix, error analysis for triangular matrix 262—267 Inverse matrix, high-accuracy computation of 281 Inverse matrix, Newton's method for 278 Inverse matrix, Schulz iteration 278 Inverse matrix, Strassen's method for 448—449 478—479 Inverse matrix, times for computation on early computers 272 Inverse matrix, triangular, bounds for 147—149 Inverse matrix, triangular, methods for 262—267 Inverse matrix, why not to compute 260 Involutary matrix 519 Ipsen, Use C.F. 123 129 133 376 377 Iri, Masao 49 485 Irreducible matrix 127 Isaacson, Eugene 186 257 Itanium chip 46 Iterative methods see also “Stationary iterative methods” Iterative methods dates of publication 322 Iterative methods error analysis 325—335 Iterative methods error analysis, survey of 323—324 Iterative methods stopping criteria 335—337 467—468 Iterative refinement backward error analysis 235—239 463 Iterative refinement for least squares problem 388—391 403 Iterative refinement for square linear system 27 184 231—243 462—463 Iterative refinement for Vandermonde system 427—428 Iterative refinement forward error analysis 232—235 463 Iterative refinement in fixed precision 179 234 494 Iterative refinement in mixed precision 234 Iterative refinement LAPACK convergence test 241 Iterative refinement practical issues 241—242 Iterative refinement with QR factorization 368—369 Iterative refinement, condition number estimate from 242 Jacobi method, forward error analysis 328—329 Jalby, William 376 Jankowski, M. 85 240 241 Jansen, Paul 483 Jennings, A. 152 Jennings, L.S. 413 Johnson, Charles R. 107 115 137 152 284 306 342 543 547 551 554 Johnson, Samuel 667 Jones, Mark T. 227 Jones, William B. 505 Jordan canonical form 340 Jordan, Camille 281 Jordan, T.L. 402 Jordan, Wilhelm 281 Kagstroem, Bo 302 315 316 318 Kahan matrix 149 205 Kahan matrix second smallest singular value 154 Kahan, William M. (Velvel) 1 26 29 30 32 42 43 44 45 49 55 58 59 60 69 78 83—86 88 103 111 114 124 149 152 157 226 242 404 483 486 491 494—496 498 499 504 Kahaner, David K. 381 Kailath, T. 429 Kala, R. 318 Kaniel, S. 227 Kaporin, Igor 447 Karasalo, Ilkka 152 Karatsuba, A. 447 Karlin, Samuel 520 Karlson, Rune 392 404 406 Karney, David L. 512 522 Karp, A. 187 Karpinski, Richard 52 495 Kato, Tosio 115 Kaufman, Linda 213 216 226 227 376 Kaufmann, Matt 56 Kearfott, R. Baker 483 Keiper, Jerry B. 31 Keller, Herbert Bishop 186 257 321 Kelley, C.T. 468 476 Kennedy, Jr., William J. 29 Kenney, Charles S. 298 318 523 Kerr, Thomas H. 210 Kielbasihski, Andrzej 77 85 209 241 393 404 410 414 Kincaid, D.R. 499 Kiriljuk, O.P. 285 Kittaneh, Fuad 523 Knight, Philip A. 324 347 349 351 447 448 Knuth, Donald E. xxiii xxviii 49 53 54 61 79 84 85 104 447 471 489 518 523 532 Kocak, Hiiseyin 29 Koltracht, L. 128 129 Koq, O.K. 103 Korner, T.W. 451 Kornerup, Peter 49 Kosowski, Przemyslaw 525 Kostin, V.I. 285 Kostlan, Eric 516 524 Kovarik, Z.V. 132 Kowalewski, G. 428 Krasny, Robert 502 Kreczmar, Antoni 446 Kreiss matrix theorem 346 Krogh, F.T. 499 Kronecker product 306 317 Krueckeberg, F. 191 Kubota, Koichi 485 Kucherov, Andrey B. 209 Kuczyriski, J. 298 Kuki, H. 56 Kulisch, Ulrich W. 483 Kuperman, I.B. 132 La Porte, M. 486 La Touche, Mrs. 79 80 Laderman, Julian 437 446 Laeuchli, Peter 379 Lagrange, Joseph Louis 215 Lancaster, Peter 317 468 LANCELOT 170 189 Lanczos, Cornelius 486 Langlois, Philippe 484 LAPACK 579—581 LAPACK, 497—498 LAPACK, block 228 LAPACK, block and partitioned LU factorization 257 LAPACK, Cholesky factorization 210—211 LAPACK, condition number estimation 292—294 303 LAPACK, forward error bound for linear systems 131 LAPACK, iterative refinement 241—242 LAPACK, least squares problem 405
Реклама
 |
|
О проекте
|
|
О проекте



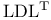 factorization
factorization 
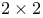 problems, solving
problems, solving