Авторизация
Поиск по указателям
Higham N.J. — Accuracy and Stability of Numerical Algorithms
Обсудите книгу на научном форуме Нашли опечатку?
Название: Accuracy and Stability of Numerical AlgorithmsАвтор: Higham N.J. Аннотация: What is the most accurate way to sum floating point numbers? What are the advantages of IEEE arithmetic? How accurate is Gaussian elimination and what were the key breakthroughs in the development of error analysis for the method? The answers to these and many related questions are included here.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2Год издания: 2002Количество страниц: 680Добавлена в каталог: 19.06.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Second difference matrix 522 Semiconvergent matrix 332 Seminormal equations for least squares problem 391—392 Seminormal equations for under determined system 408 Separation (sep) of two matrices 313 Sha, Xuan-He 437 446 Shampine, Lawrence F. 29 76 86 524 Shannon, Claude E. 56 Shapiro, Alexander 133 Shepherd, David 56 Sherman — Morrison formula 190 487 Sherman — Morrison — Woodbury formula 258 558 Shewchuk, Jonathan Richard 29 91 Shinnerl, Joseph R. 226 229 Shroff, Gautam M. 299 Shub, Michael 133 516 Sierpinski gasket 521 Significance arithmetic 486 Significand 36 Significant digits correct 3—4 28 Significant digits least and most significant 36 Simon, Horst D. 446 447 Singular value decomposition (SVD) 114—115 Skeel, Robert D. 31 123 133 178 186 187 190 231 235 240 482 Skew-symmetric matrix 214 225 Slishman, Gordon 446 569 Sloane, N.J.A. 168 Smale, Steve 2 Smith, David M. 502 Smith, Francis J. 103 427 Smith, Jon M. 32 Smith, Robert L. 500 506 Smith, Roger M. 446 569 Smoktunowicz, Alicja 85 129 136 241 404 525 Snyder, James N. 231 240 Software avoiding underflow and overflow 499—501 Software effects of underflow 501 Software issues in floating point arithmetic 489—509 Software portability 496—499 Software specifying arithmetic parameters 496—497 Software specifying numerical constants 498 Sokolnicka, Jolanta 241 SOR method, forward error analysis 329 Sorensen, Danny C. 180 187 226 228 256 Sorevik, T. 448 Spencer, Herbert 657 Spiefi, J. 446 Spooner, David 485 Square root, of complex number 32 Stability see “Backward stability” “Forward Stable algorithms, designing 26—28 Stationary iterative methods 321—337 Stationary iterative methods and powers of a matrix 351 Stationary iterative methods backward error analysis 330—331 Stationary iterative methods forward error analysis 325—329 Stationary iterative methods scale independence 327 Stationary iterative methods singular systems 333—335 Stationary iterative methods stopping criteria 335—337 Stationary iterative methods, Jacobi method 328—329 Stationary iterative methods, singular systems, theory for 331—333 Stationary iterative methods, SOR method 329 Statistics see also “Variance” Statistics, computational references 29 Steele, Jr., Guy L. 57 Stegun, Irene A. 30 Sterbenz, Pat H. 29 30 45 53 56 486 Stewart, G.W. (Pete) xxviii 68 102 107 115 119 126 133 139 152 163 187 190 209 231 240 241 282 295 302 307 318 339 351 373 374 376 377 382 384 397 400 402—404 500 517 525 Stewart, Michael 210 Stewart, William J. 302 Sticky bit 41 Stockmeyer, Larry J. 102 Stoer, Josef 76 107 114 116 187 Stone, Betty Jane 114 Storey, C. 317 Stoutemyer, David R. 486 Strakos, Zdenek 324 Strang, Gilbert 13 112 133 457 Strassen's method 434—436 Strassen's method error analysis 440—443 Strassen's method error versus operation count 14 Strassen's method for inversion 448—449 478—479 Strassen's method implementation issues 446—447 Strassen's method Winograd's variant 435—436 442—443 Strassen's method, accuracy compared with conventional multiplication 441—442 Strassen, Volker 278 434 448 449 Straus, E.G. 126 133 Street, Anne Penfold 168 Stufken, John 168 Stummel, Friedrich 30 76 187 Subdifferential, of a vector norm 289 Subgradient 290 Subnormal numbers 37 42 492 Substitution, back and forward 140—141 Subtraction, exactness in floating point arithmetic 45 Successive overrelaxation method see “SOR method” Summation 79—92 Summation, choice of method, summary 89—90 Summation, compensated and applications 83—88 Summation, condition number 91 Summation, criterion for minimizing error 82 Summation, distillation algorithms 88 Summation, doubly compensated 87—88 Summation, error analysis 81—83 Summation, insertion method 80 Summation, pairwise (fan-in) 80 Summation, recursive 80 Summation, recursive, ordering in 17 82—83 Summation, statistical error estimates 88—89 Sun, Ji-guang 107 115 119 126 129 133 181 190 201 209 374 377 382 384 392 400 402 404 406 411 414 429 Sun, Xiaobai 282 376 Sun, Zheng 411 414 SVD (singular value decomposition) 114—115 Swann, W.H. 472 Swartzlander, Jr., Earl E. 49 Sweeney, D.W. 56 Swenson, J.R. 48 Sylvester equation 306 Sylvester equation backward error 308—311 Sylvester equation Bartels — Stewart method 307—308 Sylvester equation generalizations 316—318 Sylvester equation perturbation theory 313—315 Sylvester equation practical error bounds 315—316 Sylvester equation solution methods 307—308 Sylvester, James Joseph 305 317 434 Symbolic manipulation package 6 Symbolic Math Toolbox 3 6 463 514 519 Symmetric indefinite factorization see “Block Symmetric indefinite matrix 214 Symmetric positive definite matrix 196 Symmetric positive definite matrix and block LU factorization 255—256 Symmetric positive definite matrix, practical test for 210 Symmetric positive semidefinite matrix 201 Symmetric positive semidefinite matrix, determinantal conditions for 211 Symmetric quasidefinite matrix 229 Synthetic division 96 Tablemaker's dilemma 4 50 Tang, Ping Tak Peter 50 496 528 Tang, W.P. 429 Tao, Pham Dinh 116 301 Tartaglia, Niccolo 479 Tasche, Manfred 456 Taussky, Olga 511 514 Test for accuracy of floating point arithmetic 51—52 Test for guard digit 52 Test matrices 511—525; see also “MATLAB” “Matrix” “Random Test matrices, Harwell — Boeing collection 524 Test matrices, Matrix Computation Toolbox 583—585 Test matrices, Matrix Market 524 Teukolsky, Saul A. 476 487 505 Thacher, Jr., Henry C. 188 Thisted, Ronald A. 29 Thompson, Sir D'arcy Wentworth 1 Threshold pivoting 193 Thron, W.J. 505 Tienari, Martti 49 Tisserand, Arnaud 50 Tisseur, Franchise 294 461 462 468 523 Todd, John 114 115 512 518 523 524 Toeplitz matrix, pseudospectra 525 526 Toeplitz matrix, tridiagonal 521—522 Toh, Kim-Chuan 480 523 Toledo, Sivan 248 Torczon, Virginia J. 472 475 476 Tornheim, L. 169 170 Totally nonnegative matrix 164 520 Totally nonnegative matrix, LU factorization 164—165 188 Totally nonnegative matrix, row scaling in 179 Totally nonnegative matrix, test for 188 Transformations, well conditioned 27 Traub, J.F. 428 Trefethen, Lloyd N. 5 157 168 169 180 323 337 339 340 342 345 346 348 350 351 480 516 523 525 Tremaine, Scott 87 Triangular matrix, bounds for inverse 147—149 Triangular matrix, condition numbers 142—143 Triangular matrix, inversion methods, blocked 265—267 Triangular matrix, inversion methods, unblocked 262—264 Triangular matrix, M-matrix 145—147 Triangular systems 139—155 Triangular systems conditioning 144—145 Triangular systems fan-in algorithm 149—151 Triangular systems partitioned inverse method 153 Triangular systems substitution, backward error analysis 140—142 Triangular systems substitution, forward error analysis 142—147 Triangular systems, accurate solution of 139 143 144 147 Tridiagonal matrix 174—176 Tridiagonal matrix, condition number estimation 299—301 Tridiagonal matrix, growth factor 173 Tridiagonal matrix, LU factorization 174 Tridiagonal matrix, LU factorization, error analysis of 174—176 Tridiagonal matrix, structure of inverse 300—302 Tridiagonal matrix, Toeplitz 521—522 Tropp, Henry S. 489 Trossett, Michael W. 472 Trummer, Manfred R. 340 348 350 Truncation error 5 Tsao, Nai-kuan 76 375 Tucker, Warwick 482 Tukey, John W. 56 456 Turing Award of the ACM xxix 55 Turing programming language 503 Turing programming language, Numerical Turing 503 Turing, Alan Mathison xxix xxx 29 114 119 184 185 281 481 Turing, Alan Mathison, contributions in 1948 paper “Rounding-off errors” 184—185 281 Turnbull, H.W. 374 521 Turner, Peter R. 47 49 152 Twisted factorization 303 Tyrtyshnikov, Evgenij E. 523 Ulp (unit in last place) 39 Uncertainty, in data 5 Under determined system 408 Under determined system backward error, normwise 411 Under determined system backward error, row-wise 411 Under determined system, modified Gram — Schmidt 413 Under determined system, perturbation theory 409—411 Under determined system, Q method (QR factorization) 408 Under determined system, Q method (QR factorization), error analysis 411—413 Under determined system, seminormal equations 408 Under determined system, seminormal equations, error analysis 412 Underflow 16 38 Underflow, avoiding 499—501 Underflow, effects on software 501 Underflow, gradual 38 42 45 56 Underflow, model for error analysis 56—57 Underhill, L.G. 524 525 Ungar, Peter 447 UNICOS library (Cray) 436 438 Unit roundoff 3 38 Update formula, involving small correction 27 Urabe, Minoru 57 Uspensky, J.V. 487 Vajtersic, M. 448 van de Geijn, Robert 282 van der Sluis's theorem 125 van der Sluis, A. 125 126 190 199 381 402 Van der Vorst, Henk A. 187 226 256 324 van Leeuwen, J. 447 Van Loan, Charles F xxviii 24 102 115 129 132 136 172 187 208 210 228 231 256 297 307 308 308 339 342 345 352 363 365 375 377 380 382 397 402 405 451 452 456 van Veldhuizen, M. 189 van Wijngaarden, A. 498 Vancouver Stock Exchange, inaccurate index 54 Vanderbei, Robert J. 229 Vandermonde matrix bounds and estimates for condition number 417—418 Vandermonde matrix definition 416 Vandermonde matrix inverse 416—418 Vandermonde matrix inversion algorithm 417 Vandermonde matrix LU factorization in factored form 422 Vandermonde matrix QR factorization 429 Vandermonde matrix structured condition number 428—429 Vandermonde system 415—431 Vandermonde system accuracy independent of condition number 425 Vandermonde system algorithm for dual 421 Vandermonde system algorithm for primal 422—423 Vandermonde system algorithm for residual of confluent system 427 Vandermonde system backward error analysis 425—426 Vandermonde system complexity results 429 Vandermonde system curing instability 427—428 Vandermonde system forward error analysis 424—425 Vandermonde system history of solution methods 429 Vandermonde system preventing instability 426—427 Vandermonde system structured backward error 429 Vandermonde-like matrix, confluent, definition 419 Vandermonde-like matrix, definition 418 Vandermonde-like matrix, determinant 430 Varah, James M. 133 154 257 Varga, Richard S. 147 154 257 505 Variance, algorithms for computing 11—12 29 Variance, condition numbers for 32 Variance, error bound for two-pass formula 33 Vavasis, Stephen A. 278 395 Vec operator 306 Vec-permutation matrix 314 317 584 Vemulapati, Udaya B. 299 397 Venus probe, loss due to program bug 489 Verdonk, Brigitte 496 Verschaeren, Dennis 496 Veselic, Kresimir 210 Vetterling, William T. 476 487 505 Vieta, Franciscus 479 Vignes, J. 486 Viswanath, D. 516 Vitasek, Emil 90 Viten'ko, I.V. 86 von Neumann, John 29 48 183 184 188 260 515 Waite, William 495 496 Walden, Bertil 392 404 406 Walker, Homer F. 323 468 Wallis, Jennifer Seberry 168 Wallis, W.D. 168 Ward, Robert C. 282 Warming, Robert F. 525 Wasilkowski, G.W. 133 Wasniewski, Jerzy 302 Watson, G.A. 133 Watterson, Bill 471 Wedderburn, J.H.M. 10 Wedin's least squares perturbation theorem 382 Wedin's least squares perturbation theorem, proof 400—402 Wedin, Per-Ake 382 400 402 405 413 Wegert, Elias 346 Wei, Musheng 380 402
Реклама
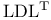factorization (of symmetric matrix)”
|
|
О проекте