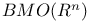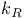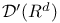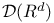Авторизация
Поиск по указателям
Bogachev V.I. — Measure Theory Vol.2
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure Theory Vol.2Автор: Bogachev V.I. Аннотация: Measure theory is a classical area of mathematics born more than two thousand years ago. Nowadays it continues intensive development and has fruitful connections with most other fields of mathematics as well as important applications in physics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2007Количество страниц: 500Добавлена в каталог: 22.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Scheffe H. I: 134 428 Scheffe theorem I: 134. 428 Scheffer C.L. I: 431 Scheme, Souslin I: 36 Scheme, Souslin, monotone I: 36 Scheme, Souslin, regular I: 36 Schief A. II: 228 260 454 Schikhof W.H. I: 406 414 Schilling R. I: 414 Schlesinger L. I: 411 Schlumprecht T. I: 215 239 Schmets J. I: 413 Schmetterer L. I: 412 Schmitz N. I: 414 Schmuckenschlager M. I: 246 Schneider R. I: 431 Schoenflies A. I: 410 Schuss Z. II: 160 Schwartz J.T. I: 240 282 283 321 413 415 421 423 424 434 435; 264 326 373 447 463 Schwartz L. I: 376 414; 443 447 452 455 462 Schwarz G. I; 141 428 Scorza Dragoni G. II: 137 Second mean value theorem I: 150 Section of a mapping II: 34 Section of a set I: 183 Seebach J. II; 9 64 Segal I.E. I: 312 327 414 Segovia C. II: 320 451 Seidei W. II: 450 Selection II: 34 35 Selection, Borel II: 38 Selection, measurable II: 33 34 35 40 11 441 458 Selection, Michael’s II: 228 229 Semadeni Z. II: 452 Semenov P.V. II: 228 Semi-algebra of sets I: 8 Semi-ring of sets I: 8 Semiadditivity I: 9 Semicontinuity, lower II: 75 Semicontinuity, upper II: 19. 75 Semifinite measure I: 97 312 Seminorm I: 249 Semmes S. I: 437 Sentilles F.D. II: 455 Separable in the sense of Rohlin II: 280 Separable measure I: 54 91 306; Separable metric space I: 252 Separable, II: 16 Sequence, convergent, in I: 128 Sequence, convergent, in measure I: 111 Sequence, convergent, in the mean I: 128 Sequence, fundamental, in I: 116 128 Sequence, fundamental, in measure I: 111 Sequence, fundamental, in the mean I: 116 128 Sequence, uniformly distributed II: 238 Sequence, weakly convergent I: 281; II L75 Sequence, weakly fundamental II: 175 209 Sequential compactness II: 5 Sequentially Prohorov space II: 219 Serov V.S. I: 415 Set function, additive I: 302 Set function, countably additive I: 9 Set function, countably-subadditive I: 11 Set function, monotone I: 17 41 70 71 75 Set function, subadditive I: 9 Set of continuity of a measure II: 186 Set of full measure I: 110 Set of measures, countably determined II: 230 Set of measures, countably separated II 230 Set, I: 36; II: 46 Set, I: 36; II: 46 Set, II: 49 Set, II: 49 Set, II: 49 Set, I: 17 21 Set, analytic I: 36; II: 20 46 Set, Baire II: 12 Set, Bernstein I: 63 Set, Besicovitch I: 66 Set, Borel I: 6; II: 10 Set, bounded perimeter I: 378 Set, Caccioppolli I: 378 Set, Cantor I: 30 Set, closed I: 2 Set, co-Souslin II: 20 Set, coanalytic II: 20 Set, cylindrical I: 188; II: 117 Set, direcled II: 3 Set, Erdoes I: 422 Set, functionally closed II: 4 12 Set, functionally open II: 12 Set, Lebesgue I: 352 Set, Lebesgue measurable I: 3 17 Set, locally measurable I: 97 Set, measurable I: 21 Set, measurable, Caratheodory I: 41 Set, measurable, Jordan I: 2 Set, measurable, with respect to u: I: 17 Set, Nikodym I: 67 Set, nonmeasurable I: 31 Set, open I: 2 Set, ordered I: 62 Set, partially ordered I: 62 277 Set, perfect II: 8 Set, Sierpinski I: 91 Set, Souslin I: 36 39 420; 46 Set, symmetric II: 119 Set, universally measurable II: 68 Set, universally Radon measurable II: 68 Set, well-ordered I: 62 Set-theoretic operation I: 1 Set-theoretic problem I: 77 Sets, independent II: 400 Sets, metrically separated I: 194 Severini C. I: 426 Shabunin M.I. I: 415 Shah S.M. I: 414 Shakarchi R. I: 414 Shavgulidae E.T. II: 449 Sheftel Z.G. I: 413 Shelah S. II: 376 Sherman S. II: 400 Shilov G.E. I: 397 414 437 438; 446 Shiryaev A.N. I; vi 411; 410 453 461 Shneider (Sneider) V.E. II: 440 Shortt P.M. II: 50 60 61 159 456 Sicbert E. II: 451 Sicrpiriski W. I: 48 78 82 91 232 395 409 417 419 422 428; 57 60 160 237 439 440 442 444 451 Sidak Z. II: 428 Sierpiiiski set I: 91 Sierpiiiski theorem I: 48 421 Signed measure I: 175 SikoTBki R. I: 414 421; 326 450 451 Simon A.B. II: 333 Simon L. I: 437 Simonelli I. I: 103 Simonnet M. I: 414 Simonovits M. I: 173 Simple function I: 106 Sinai Ya.G. II: 391 464 Singular measure I: 178 Singularity of measures I: 178 Sinitsyn I.N. I: 414 Sion M. I: 414 423 430; 139 440 444 460 463 Skala H.J. II: 324 461 Skorohod (Skorokhod) A.V. I: viii 413; 98 199 448 452 453 Skorohod property II: 199 Skorohod represent at ion II: 199 Skorohod theorem II: 199 Slowikowski W. II: 448 Slutsky E. I: 171 426; Smiley M.F. I: 422 Smirnov V.I. I: 412 426 435 Smital J. I: 403 Smith H.J.S. I: 419 Smith H.L. I: 435 Smolenski W. II: 451 Smolyanov O.G. II: 125 167 410 448 449 451 456 Smuhan V.L. I: 282 434 Sobolev derivative I: 377 Sobolev inequality I: 377 378 Sobolev S.L. I: 325 376 Sobolev space I: 377 Sobolev V.I. I: 414 Sodnomov B.S. I: 87; II: 60 Sohrab H.H. I: 414 Sokal A.D. II: 462 Solntsev S.A. II: 448 Solovay R. I: 80 Sondermann D. II: 452 Sorgenfrey interval II: 9 Sorgenfrey line II: O Sorgenfrey plane II: 9 Sorgenfrey R.H. II: 9 Soucek J. I: 379; II: 231 252 Soury P. II: 456 Souslin M. I: vii viii 35 417 420; 439 Souslin operation I: 36 Souslin scheme I: 36 Souslin scheme, monotone I: 36 Souslin scheme, regular I: 36 Souslin set I: 39 420; 46 Souslin space II: 20 Space of measures I: 273 Space, I: 373 Space, II: 56 Space, I: 306 Space, II: 55 Space, II: 55 Space, II: 5 Space, almost Lindeloef II: 131 Space, Banach I: 249 Space, Banach, reflexive I: 281 Space, barrelled II: 123 Space, Borel measure-complete II: 135 Space, Cech complete II: 5 Space, compact II: G Space, complete mod0 with respect to a basis II: 282 Space, complete with respect to a basis II: 280 Space, completely regular II: 4 Space, countably compact II: 5 Space, countably paracompact II: Space, double arrow II: 9 Space, dual I: 256 262 281 283 311 313 Space, dyadic II: 134 Space, Euclidean I: 254 Space, Frechet II: 2 Space, Hauadurfi II: 4 Space, hemicompact II: 220 Space, Hilbert I: 255 Space, Lebesgue — Rohlin II: 282 Space, Lindeloef II: 5 Space, locally compact II: 5 114 Space, Lorentz I: 320 Space, Lusin II: 12 Space, Marik II: 131 Space, measurable I: 4 Space, measure-compact II: 131 Space, metric, complete I: 243 Space, metric, separable I: 252 Space, metrizable II: 2 Space, Milyutin II: 201 Space, normal II: 4 Space, normed I: 249 Space, normed, complete I: 249 Space, normed, uniformly convex I: 2N4 Space, Orlicz I: 320 Space, paracompact II: 5 Space, perfectly normal II: 4 Space, Polish II: 6 Space, probability I: 10 Space, Prohorov II: 219 455 Space, quasi-dyadic II: 134 Space, quasi-Marik II: 131 Space, Radon II: 135 Space, regular II: 4 Space, separable in the sense of Rohlin II: 280 Space, sequentially Prohorov II: 219 Space, Sobolev I: 377 Space, Souslin II: 20 Space, standard measurable II: 12 Space, two arrows II: 9 Spiegel M.R. I: 414 Sprecher D.A. I; 414 Srinivasan T.P. I: 94 414 419 420 Srivastava S.M. II: 440 Staircase of Cantor I: 193 Standard, Gaussian measure I: 198 Standard, measurable space II: 120 Starnpacchia G. I: 160 Steen L. II: 9 64 Steen P. van der I: 414; II: 446 Stegall Gh. II: 167 Stein EM. I: 65 238 320 353 367 374 375 379 386 398 414 430 431 436 Stein J.D. II: 244 Steinbaus H. I: 85 100 102 264 430 431; 457 464 Steiner J. I: 212 Steiner’s symmetrization I: 212 Stepanoff W. I: 438 Stepin A.M. II: 459 Stieltjes I: 33 152 Stiertjcs T.J. I: 33 152 416 425 Stochastically independent mappings II: 399 Stolz O. I: 417 Stone A.H. II: 60 Stone condition II: 105 Stone M.H. I: viii 411 423; 77 104 326 376 442 445 461 Stone representation II: 326 Stone theorem II: 326 Stone — Cech compact ideation II: 5 Stopping time II: 353 Strassen theorem II: 236 Strassen V. II: 236 324 461 Strauss W. II: 463 Strict inductive limit II: 207 Strieker C. II: 63 Stromberg K. I: 81 325 402 414 435; Strong lifting II: 406 Strong moment of a measure II: 142 Strong topology II: 124 Stroock D.W. I: 414; II: 433 453 Structure I: 277 Structure, I: 277 Structure, complete I: 277 Sturm K.-T. II: 454 Stute W. I: 413; II: 453 Subadditivity I: 9 Subadditivity, countable I: 11 Sublinear function I: 67 Submartingale II: 348 Submeasure I: 75 Submeasure, Maharam I: 75 Submodular set function I: 75 Subramanian B. I: 31(1 Sucheston L. I: 435 438; 463 Sudakov V.N. I: 318 434; 448 461 Suetin P.K. I: 261 Sullivan D. I: 422 Sullivan J.A. I: 413 Sultan A. II: 131 451
Реклама
 |
|
О проекте
|
|
О проекте



 -algebra
-algebra 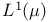
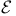 -analytic
-analytic  -analytic
-analytic  -analytic
-analytic  -measurable
-measurable