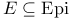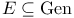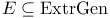|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adamek J., Herrlich H., Stecker G.E. — Abstract and Concrete Categories - The Joy of Cats |
|
|
 |
| Предметный указатель |
(ConGen, Initial Mono-Source)-factorizable category 17J
(ConGen, Initial Mono-Source)-functor, vs. concretely co-wellpowered 17.11
(E, 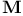 )-diagonalization property 15.1 )-diagonalization property 15.1
(E, 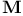 )-factorization 15.1 )-factorization 15.1
(E, M)-category 15.1
(E, M)-category vs. (E, M)-factorization 15.10
(E, M)-category vs. (E, M)-functor 17.4
(E, M)-category vs. co-wellpowered category 15.25 15.26
(E, M)-category vs. extremally co-wellpowered category 15.25 15.26
(E, M)-category vs. mono-source 15.6—15.9
(E, M)-category vs. regular epimorphism 15.7
(E, M)-category vs. strongly complete category 15.25 15.26
(E, M)-category vs. topological category 21.14
(E, M)-category, conditions on E 15.14 15.15
(E, M)-category, consequences of 15.5
(E, M)-category, implies 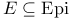 15.4 15.4
(E, M)-category, values for E and M 15.8
(E, M)-diagonalization property 14.1
(E, M)-factorization 14.1
(E, M)-factorization vs. (E, M)-category 15.10
(E, M)-factorization vs. (E, M)-structured category 14.7
(E, M)-factorization vs. faithful functor 17.15 17.16
(E, M)-factorization vs. topological category 21.16 21.17
(E, M)-factorization, uniqueness 15.5
(E, M)-functor vs. (E, M)-category 17.4
(E, M)-functor vs. has (E, M)-factorizations 17.10
(E, M)-functor vs. topologically algebraic functor 25.6
(E, M)-functor, = adjoint functor 17.3 18.3 18.4
(E, M)-functor, implies 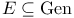 17.6 17.6
(E, M)-functor, implies factorizations are essentially unique 17.7
(E, M)-functor, implies M determines E 17.7
(E, M)-functor, M need not be closed under composition nor determined by E 17.8
(E, M)-functor, not every functor is 17.4
(E, M)-functor, properties of 17E
(E, M)-structured category 14.1 ff
(E, M)-structured category vs. (E, M)-factorization property 14.7
(E, M)-structured category vs. (extremal) epimorphisms 14.10—14.14
(E, M)-structured category vs. composition of morphisms 14.6
(E, M)-structured category vs. extremal monomorphisms 14.10
(E, M)-structured category vs. isomorphisms 14.5
(E, M)-structured category, consequences of 14.6 14.9 14.11
(E, M)-structured category, duality for 14.3
(E, M)-structured category, relationship to limits 14.15 ff
(E, M)-structured category, relationship to special morphisms 14.10 ff
(E, M)-structured category, uniqueness of factorizations 14.4
(E, Mono)-structured category, vs. regular epimorphism 14.14
(E, Mono-Source)-category, vs. (Epi, M)-category 15.11
(E, Mono-Source)-functor, implies 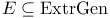 17.9 17.9
(E, —)-category 15B 15D
(E, —)-functor 17.4
(E, —)-structured category 14H
(Epi, ExtrMono)-structured category vs. equalizer 14.19
(Epi, ExtrMono)-structured category vs. intersection 14.19
(Epi, ExtrMono-Source)-category, characterization 15.16
(Epi, ExtrMono-Source)-category, strongly complete category is 15.17
(Epi, ExtrMono-Source)-category, vs. (ExtrEpi, Mono-Source)-category 15C
(Epi, Initial Source)-factorizable category vs. topologically algebraic category 25.6
(Epi, M)-category, characterization 15.16
(Epi, M)-category, characterization vs. (E, Mono-Source)-category 15.11
(Epi, Mono-Source)-factorizable category vs. algebraic category 23.30 23.31
(Epi, Mono-Source)-factorizable category vs. essentially algebraic category 23.8 23.9
(Epi, Mono-Source)-factorizations vs. monadic category 20.49
(Epi, Mono-Source)-factorizations, imply (ExtrEpi, Mono-Source)-category 15.10
(ExtrEpi, Mono-Source)-category vs. (Epi, ExtrMono-Source)-category 15C
(ExtrGen, Mono)-factorization 17I
(ExtrGen, Mono-Source)-functor 17K
(ExtrGen, Mono-Source)-functor vs. preservation of strong limits 17.11 17H
(Generating, M)-functor vs. adjoint functor 18.4
(Generating, Mono-Source)-factorizations of 2-sources vs. reflection of isomorphisms 17.13
(Generating, —)-factorizable functor, composites of 17B
(Generating, —)-factorization, for 2-sources implies preservation of mono-sources 17.12
(RegEpi, Mono)-structured category 14.22 14D
(RegEpi, Mono-Source)-category vs. regular factorization 15.13
(RegEpi, Mono-Source)-category, characterization 15.25
(Strongly Generating, Initial Source)-functor, is topologically algebraic functor 25.6
Absolute coequalizer 20.14
Absolute colimit 20.14
Absolute retract 9.6
Absolute retract vs. enough injectives 9.10
Adjoint functor 18.1 ff
Adjoint functor theorem, concrete 18.19
Adjoint functor theorem, first 18.12
Adjoint functor theorem, special 18.17
Adjoint functor vs. (Generating, M)-functor 18.4
Adjoint functor vs. adjoint situation 19.1 19.4 19.8
Adjoint functor vs. algebraic category 23.31
Adjoint functor vs. co-adjoint functor 18A 19.1
Adjoint functor vs. co-wellpoweredness 18.11 18.14 18.19
Adjoint functor vs. colimit 18D
Adjoint functor vs. completeness 18.12 18.14 18.17 18.19
Adjoint functor vs. essentially algebraic functor 23.8
Adjoint functor vs. exponential functor 27.7
Adjoint functor vs. extremal monomorphism 18J
Adjoint functor vs. free object 18.19
Adjoint functor vs. full, faithful functor 19I
Adjoint functor vs. monadic category 20.46
Adjoint functor vs. monadic functor 20.12 20.17
Adjoint functor vs. reflection of epimorphisms 18I 19B
Adjoint functor vs. regularly algebraic category 23.38
Adjoint functor vs. representable functor 18C
Adjoint functor vs. solid functor 25.12 25.19
Adjoint functor vs. topologically algebraic functor 25.3 25.6 25.19
Adjoint functor vs. wellpoweredness 18.19
Adjoint functor, between posets 18H
Adjoint functor, characterization theorems 18.12 18.14 18.17 18.19
Adjoint functor, characterizations 18.3
Adjoint functor, comparison functor for 20.38 20.42
Adjoint functor, composition of 18.5
Adjoint functor, monadic functor is 20.12
Adjoint functor, preserves mono-sources and limits 18.6 18.9
Adjoint functor, smallness conditions for 18B
Adjoint sequence 19F
Adjoint situation 19.3 ff
Adjoint situation gives rise to a monad 20.3
Adjoint situation induced by (co-)adjoint functor 19.7
Adjoint situation uniqueness 19.9
Adjoint situation vs. adjoint functor 19.1 19.4 19.8
Adjoint situation vs. equivalence functor 19.8 19H
Adjoint situation vs. free object 19.4
Adjoint situation vs. Galois correspondence 19.8
Adjoint situation vs. indiscrete structure 21A
Adjoint situation vs. monad 20A
Adjoint situation vs. reflective subcategory 19.4
Adjoint situation vs. universal arrow 19.7
Adjoint situation, alternative description 19A
Adjoint situation, associated with a monad 20.7
Adjoint situation, composition of 19.13
Adjoint situation, consequences of 19.14
Adjoint situation, duality for 19.6
Adjoint situation, lifting of 21.26 21.28
Adjoint, for a functor 19.10
Algebra, partial binary 3.52
Algebraic category 23.19 ff 23D
Algebraic category vs. (Epi, Mono-Source)-factorizable category 23.30 23.31
Algebraic category vs. adjoint functor 23.31
Algebraic category vs. extremal co-wellpoweredness 23.27
Algebraic category vs. extremal epimorphism 23.30
Algebraic category vs. unique lift of (ExtrEpi, Mono-Source)-factorizations 23.31
Algebraic category, characterization theorem for 23.30 23.31
Algebraic category, concrete functor between 23.22
Algebraic category, implies extremal epimorphisms are final 23.23
Algebraic construct vs. monadic construct 23.41
Algebraic construct, = regular epireflective subconstruct of monadic construct 24.3
Algebraic construct, bounded, vs. bounded quasivariety 24.11
Algebraic functor 23.19 ff
Algebraic functor, closed under composition 23.21
Algebraic functor, need not preserve regular epimorphisms 23.25 23J
Algebraic functor, reflects regular epimorphisms 23.24
Algebraic functor, restrictions of 23L
Algebraic functor, vs. composite of regular monadic functors 24.2
| Algebraic functor, vs. regular epimorphism 23J
Algebraic functor, vs. regular factorization 24.2
Algebraic functor, vs. uniquely transportable functor 23.30
Algebraic hull of a concrete category 23K
Algebraic subcategory vs. extremally epireflective subcategory 23.33
Algebraic subcategory, conditions for 23.32 23.33
Algebraic theory 20C
Algebraic-topological decompositions 26C
Algebraic-type functors, relationships among 23.42
Amnestic concrete category 5.4 ff
Amnestic concrete category vs. Galois correspondence 6.29—6.36
Amnestic concrete category vs. topological functor 21.5
Amnestic concrete category vs. transportable concrete category 5.29 5.30
Amnestic functor 3.27 5.6 13.21 13.25 13.28
Amnestic modification, of a concrete category 5.6 5.33 5.34 5F
Amnesticity, vs. lifting of limits 13.21
Arrow category 3K 6.17
Arrow, co-universal, = co-universal costructured arrow 8.40
Arrow, costructured, = costructured arrow 8.40
Arrow, reflection, = reflection arrow 4.16
Arrow, structured, = structured arrow 8.15
Arrow, universal, = universal structured arrow 8.22
Associativity, composition of morphisms has 3.1 3.53 3C
Axiom of Choice 2.3 9A
Axiom of replacement 2.2
Axiom, topological 22.6
Balanced category 7.49 ff
Balanced category vs. extremal monomorphism 7.67
Balanced category vs. mono-source 10.12
Balanced category, topological, scarcity of 21N
Base category 5.1 ff
Bicoreflective subcategory vs. coreflective subcategory 16.4
Bicoreflective subcategory vs. separator 16.4
Bimorphism 7.49
Bimorphism vs. topological functor 21M
Bireflective subcategory 16.1
Bireflective subcategory, monoreflective subcategory is 16.3
Birkhoff-theorem 16G
Boolean ring 3.26 footnote
Cartesian closed category 27.1 ff
Cartesian closed category vs. coreflective hull 27C
Cartesian closed category vs. products of epimorphisms 27.8
Cartesian closed category vs. zero object 27A
Cartesian closed category, characterization theorem 27.4
Cartesian closed construct 27.16 ff 27D
Cartesian closed construct vs. well-fibred topological construct 27.22
Cartesian closed subcategory 27.9
Cartesian closed subcategory vs. (co)reflective subcategory 27.9
Cartesian closed topological category as injective object 27F
Cartesian closed topological category, implies base category is cartesian closed 27.14
Cartesian closed topological construct vs. powers with discrete exponents (resp. factors) 27.24
Cartesian closed topological hull 27G
Cartesian product of sets 2.1
Categorical statement involving functors, dual of 3.40 3.42
Category 3.1 ff
Category of all categories, can’t be formed because of set-theoretical restrictions 3.48
Category of concrete categories 5.15 5C
Category of objects over (resp. under) an object 3K
Category of small categories 3.47
Category of small categories is a large category 3.48
Category of small categories vs. concrete category 5I
Category of type 2 3C
Category theory, “object-free version” 3.55
Category with all products must be thin 10.32
Category, (co)complete, = (co)complete category 12.2
Category, (E, M), = (E, M)-category 15.1 ff
Category, (E, —)-structured 14H
Category, algebraic, = algebraic category 23.19 ff
Category, alternative definition 3C
Category, arrow 3K
Category, base, = base category 5.1 ff
Category, cartesian closed, = cartesian closed category 27.1
Category, co-wellpowered, = co-wellpowered category 7.87
Category, comma 3K 5.38 21F
Category, compact 18K
Category, concretely cartesian closed, = concretely cartesian closed category 27.11
Category, concretizable 5J
Category, discrete 3.26
Category, dual, = opposite category 3.5
Category, Eilenberg-Moore 20.4
Category, empty 3.3(4)
Category, essentially algebraic, = essentially algebraic category 23.5 ff
Category, exact 14F
Category, extremally co-wellpowered, = extremally co-wellpowered category 7.87
Category, extremally wellpowered, = extremally wellpowered category 7.82
Category, finitary 24.4 24.7
Category, finitely (co)complete 12.2
Category, free 3A
Category, functor-costructured 5.43
Category, functor-structured, = functor-structured category 5.40
Category, graph of 3A
Category, is a quasicategory 3.51
Category, isomorphic 3.24
Category, Kleisli 20.39 20B
Category, large 3.44
Category, locally presentable 20H
Category, monadic, = monadic category 20.8 ff
Category, non-co-wellpowered 7L
Category, object-free, = object-free category 3.53
Category, opposite, = opposite category 3.5
Category, pointed 3B 7B
Category, product 3.3(4)
Category, regular co-wellpowered 7.87—7.89
Category, regular wellpowered 7.82 7.88 7.89
Category, regularly algebraic, = regularly algebraic category 23.35 ff
Category, skeleton of a 4.12—4.15 4I
Category, small 3.44—3.45
Category, solid, = solid category 25.10 ff
Category, strongly (co)complete, = strongly (co)complete category 12.2
Category, sub- see Subcategory
Category, terminal 3.3(4)
Category, thin 3.26 3.29 3G
Category, topological, = topological category 21.7 ff
Category, topologically algebraic, = topologically algebraic category 25.1 ff
Category, total 6I
Category, universal 4J
Category, universally topological 28.16 28.18 28G
Category, wellpowered, = wellpowered category 7.82
Choice, axiom of 2.3 9A
class 2.2
Class as a category, (is not a construct) 3.3(4)
Class of all sets, = universe 2.2
Class, large, = proper class 2.2
Class, preordered 3.3(4)
Class, proper 2.2
Class, small, = set 2.2
Closed under the formation of intersections 11.26
Closed under the formation of M-sources 16.7
Closed under the formation of M-sources and E-quotients, vs. E-equational subcategory 16.17
Closed under the formation of M-sources vs. E-reflective 16.8
Closed under the formation of products and extremal subobjects, vs. (epi)reflective subcategory 16.9 16.10
Closed under the formation of products vs. E-equational subcategory 16.17
Closed under the formation of pullbacks 11.17
Closure space 5N
Co- see Dual concept
Co-adjoint functor 18.1 ff
Co-adjoint functor vs. adjoint functor 18A 19.1 19.2 19.11
Co-adjoint functor vs. colimit 18D
Co-adjoint functor vs. contravariant exponential functor 27.7
Co-adjoint, for a functor 19.10
Co-axiom, topological 22.6
Co-unit of an adjunction 19.3 19J
Co-universal arrow 8.40
Co-universal arrow vs. universal arrow 19.1 19.2
Co-wellpowered category 7.87 ff
Co-wellpowered category vs. (E, M)-category 15.25 15.26
Co-wellpowered category vs. adjoint functor 18.11 18.14 18.19
Co-wellpowered category vs. cartesian closed category 27.4
Co-wellpowered category vs. epireflective hulls 16C
Co-wellpowered category vs. essentially algebraic category 23.14
|
|
 |
| Реклама |
 |
|
|
 |
 |
|
 |
|
О проекте
|
|
О проекте



 )-diagonalization property
)-diagonalization property