Авторизация
Поиск по указателям
Dunford N., Schwartz J., Bade W.G. — Linear operators. Part 2
Обсудите книгу на научном форуме Нашли опечатку?
Название: Linear operators. Part 2Авторы: Dunford N., Schwartz J., Bade W.G.Аннотация: In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping V ↦ W between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication. An important special case is when V = W, in which case the map is called a linear operator, or an endomorphism of V. Sometimes the definition of a linear function coincides with that of a linear map, while in analytic geometry it does not.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1963Количество страниц: 986Добавлена в каталог: 18.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Set function, regular, definition III.5.11 (137) Set function, regular, properties III.5.12—14 (137—138) III.9.19—22 IV.13.75 IV.6.1—3 Set function, relativization or restrictions of III.8 Set function, singular III.4.12 (131) Set function, spaces of, as conjugate spaces IV.5.1 (258) IV.5.3 IV.6.2—3 IV.8.16 Set function, spaces of, definitions (160—162) IV.2.15—17 IV.6.1 Set function, spaces of, remarks on (389—390) Set function, spaces of, study of III.7 IV.9—10 IV.15 Set function, variation of III.1.4 (97) Set(s), III.5.1 (133) Set(s), III.4.2 (126) Set(s), Borel III.5.10 (137) Set(s), convergence of (120—127) III.9.48 Set(s), field of III.1.3 (86) Set(s), in III.7.1 (158) Set(s), Lebesgue III.4.2 (218) Set(s), open see "Open" Shapiro, J.M. 406 Shiffman, M. 88 Shohat, J.A. 1274 1276 Sikorski, R. 610 Silberstein, J.P.O. 610 Silov, G. 384 385 883 884 1161 Silverman, L.L. 75 Simple function(s), definition III.2.9 (105) Simple function(s), density in III.3.8 (125) III.8.3 III.9.46 Simple Jordan curve (225) Sin, D. 1588 Singer, I.M. 935 Singular element in a B-algebra IX.1.2 (861) Singular element in a ring (40) Singular element in a ring, non-singular operator (45) Singular set function, definition III.4.12 (131) Singular set function, derivatives of III.12.6 (214) Singular set function, Lebesgue decomposition theorem III.4.14 (132) Singularity of an analytic function (229) Sirohov, M.F. 395 Sirvint, G. 383 386 538—540 541 548 Skorohod, A. 94 Smiley, M.F. 394 395 Smith, K.T. 610 927 930 1120 Smithies, F. 548 610 1082 1083 1162 Smulian, and Eberlein theorem on weak compactness V.6.1 (430) Smulian, and Krein see "Krein — Smulian theorem" Smulian, criterion for (464) Smulian, criterion for weak compactness V.6.2 (433) Smulian, V.L. 392 395 429 430 433 434 461 463—464 465—466 472—473 612 Snol, E. 1562 1563 1587 1591 1596 1600 1601 1610 Sobczyk, A. 86 393—394 553—554 Sobolev, S.L. 1680 1686 Solomyak, M.Z. 612 Soukhomlinoff, G.A. 86 Space IV Space, B- and F-, elementary properties of II Space, B- and F-, list of special spaces IV.2 Space, B- and F-, study of IV Space, Banach see "B-space" Space, Cech compactification of IV.6.27 (279) Space, compact I.5.5 (17) Space, complete I.6.5 (19) Space, complete normed linear see "B-space" Space, completely regular IV.6.21 (276) Space, complex linear (38) (49) Space, conjugate II.3.7 (61) Space, connected I.4.12 (12) Space, dimension of (86) Space, direct sum of (88) Space, extremally disconnected (398) Space, F-space II.1.10 (51) Space, factor (38) Space, fixed point property of V.10.1 (458) Space, Hausdorff I.5.1 (15) Space, linear topological II.1.1 (49) Space, locally compact I.5.5 (17) Space, locally convex topological linear V.2.9 (417) Space, measure III.4.3 (126) Space, metric I.6.1 (18) Space, normal I.5.1 (15) Space, normal structure of V.11.14 (459) Space, normed or normed linear II.3.1 (59) Space, product I.8.1 (32) Space, real linear (38) (49) Space, reflexive II.3.22 (66) Space, regular I.5.1 (15) Space, separable I.6.11 (21) Space, subspace (36) Space, subspace spanned (36) Space, topological I.4.1 (10) Space, total, of functionals V.3.1 (418) Space, totally disconnected (41) Span, in a linear space (36) II.1.4 Sparre Andersen, E. 235 Spectral asymptotics XIII.10.G (1614) Spectral measure X.1 (888) Spectral measure, countably additive X.1 (889) Spectral measure, self adjoint X.1 (892) Spectral multiplicity theory, definition X.5 (913) Spectral radius, definition VII.8.5 (567) Spectral radius, of an element in a B-algebra IX.1.2 (861) Spectral radius, properties VII.3.4 (567) VII.5.11—18 Spectral representation, definition X.5.1 (909) XII.3.4 see Spectral set, definition VII.3.17 (572) Spectral set, of a bounded measurable function XI.4.10 (988) Spectral set, of von Neumann X.9 (933) Spectral set, properties VII.3.19—21 (574—575) Spectral synthesis, problem of XI.4 (987) Spectral theorem, for a B*-algebra X.2.1 (395) Spectral theorem, for a formally self adjoint differential operator XIII.5.1 (1333) Spectral theorem, for a normal operator X.2.4 (897) Spectral theorem, for a self adjoint differential operator with compact resolvent XIII.4.2 (1331) Spectral theorem, for an unbounded operator XII.2 (1191) Spectral theory, for compact operators VII.4 Spectral theory, in a finite dimensional space VII.1 Spectrum, X.1 (891) Spectrum, continuous VII.5.1 (580) X.8.1 Spectrum, essential, of a closed operator XIII.6.1 (1398) Spectrum, in a finite dimensional space VII.1.2 (556) Spectrum, in a general space VII.3.1 (566) Spectrum, isolated point of VII.3.15 (571) Spectrum, of a B*-algebra IX.3.4 (875) Spectrum, of an element in a B-algebra IX.1.2 (861) Spectrum, of an element of a sub B-algebra IX.1 (865) Spectrum, of an unbounded operator (599) Spectrum, of special bounded operators VII.5.2—15 (580—581) Spectrum, of special unbounded operators VII.10.1—3 (604—605) Spectrum, point VII.5.1 (580) X.3.1 Spectrum, residual VII.5.1 (580) X.3.1 Sphere, closed II.4.1 (70) Sphere, closed unit II.8.1 (59) Sphere, in a metric apace I.6.1 (19) Sreider, Y. 392 Stability of a system of differential equations VII.2.23 (564) Stasevskaya, V.V. 1588 1626 Steinhaus, H. 80—81 94 387—388 Stekloff, W. 1583 Stepanoff, W. 729 Stewart, F.M. 233 Stickelberger, L. 607 Stieltjes moment problem XII.2 (1253) Stieltjes, T.J. 132 142 929 1250 1253 1269 Stokes, G.G. 388 1527 Stone space, definition (898) Stone theorems on representation of Boolean rings and algebras I.12.1 (41) (44) Stone — Cech compactification theorem IV.6.22 (276) IX.2.16 Stone — Cech compactification theorem, remarks on (385) Stone — Weierstrass theorem IV.6.16 (272) Stone — Weierstrass theorem, complex case IV.6.17 (274) Stone — Weierstrass theorem, remarks on (383—385) Stone, and Banach see also "Banach — Stone theorem" Stone, M.H. 41 48 80 85 272 279 382 383—385 393 396 398 442 460 466 606 608 726 872 884 926 927 928 929 1243 1268 1269 1270 1272 1278 1274 1276 1277 1586 1588 1590 1591 1616 1619 Strictly convex B-space, definition VII.7 (458) Strong operator topology, definition VI.1.2 (475) Strong operator topology, properties VI.9.1—5 (511) VI.9.11—12 Strong topology, in a normed space I.3.1 (59) (419) Structure space of a B-algebra IX.2.7 (869) Sturm — Liouville operator XIII.2 (1291) XIII.9.F Sturm, C. 1291 1462 1531 1582 1583 Subadditive function, definition (618) Subbase for a topology I.4.6 (10) Subbase for a topology, criterion for I.4.8 (11) Subspace, of a linear space (36) see Summability, general principle of XIII.9.J2 (1577) Summability, of Fourier series IV.14.34—51 (331—364) Summability, of integrals IV.13.78—101 (351—356) Summability, of series II.4.31—54 (74—78) Summability, regular methods II.4.35 (75) Summability, special types of, Abel II.4.42 (76) Summability, special types of, Cesaro II.4.37 (75) II.4.39 IV.14.44 Summability, special types of, Noerlund II.4.38 (75) Summability, special types of, Poisson IV.14.47 (363) Sunouchi, G. 238 234 391 543 552 Support function, definition V.1.7 (410) Supremum, limit superior of a sequence of sets (126) Supremum, limit superior of a set of real numbers (4) Supremum, of a set of real numbers (3) Sylvester, J.J. 606—607 Symmetric difference (41) (96) Symmetric operator, definition X.4.1 (906) XII.1.7 Symmetric subspace, definition XII.4.4 (1225) Szasz, O. 384 Tagamlitzki, Y. 396 478 Takahashi, T. 388 400 Taldykin, A.T. 610 Tamarkin, J.D. 80 234—285 388 542 543 610 1118 1162 1269 1274 1276 1583 Tangent function, definition V.9.2 (446) Tangent function, examples V.11.9—13 (458—459) Tangent function, properties V.9.1 (445) V.9.3 V.11.10—11 Tangent functionals, definition V.9.4 (447) Tarski fixed-point theorem I.3.10 (8) Tarski, A. 3 Tauber, A. 78 1007 Taylor expansion for analytic functions (228) Taylor, A.E. 92 238 399 540 543 552 554 606 608 612 Taylor, B. 1582 Tchebichef, P.L. 1512 Tchebicheff polynomial (369) Teichmueller, O. 48 927 Thorin, G.O. 541 1183 Tietze extension theorem I.5.3—4 (15—17) Tietze, H. 15 Tingley, A.J. 406 Titchmarsh — Kodaira theorem XIII.5.18 (1364) Titchmarsh, E.C. 48 612 1160 1364 1586 1587 1590 1591 1592 1614 1616 1618 Titov, N.S. 93 Toeplitz, O. 75 72 80 85 399 539 609 926 928 936 1269 Tomita, M. 473 Tonelli theorem III.11.14 (194) Tonelli, L. 194 Topology, (419) Topology, base and subbase for I.4.8 (10) Topology, basic definitions I.4.1 (10) Topology, bounded V.5.3 (427) Topology, functional or V.3.2 (419) Topology, functional or V.3 Topology, linear spaces see "Operator topology" Topology, metric or strong, in a B-space (419) Topology, metric or strong, in a B-space, study of I.6 Topology, metric, definition I.6.1 (18) Topology, norm or strong, in a normed linear space II.3.1 (59) Topology, of real numbers (11) Topology, of real numbers, study of I.4—8 Topology, product, definition I.8.1 (32) Topology, topological group, definition II.1.1 (49) Topology, topological space, definition I.4.1 (10) Topology, topological space, study of I.4—8 Topology, weak* topology (462) Topology, weak, in a B-space (419) Tornhelm, L. 884 Total boundedness, in a metric space I.6.14 (22) Total differential (92) Total disconnectedness (41) Total family of functions II.2.6 (58) Total measurability, definition III.2.10 (106) see Total space of functionals, definition V.3.1 (418) Total variation of a function III.5.13 (140) Total variation of a set function III.1.4 (97) see Totally ordered set I.2.2 (4) Trace, of a finite matrix VI.9.28 (515) XI.6.8 Trace, of a matrix, definition VI.9.28 (515) Trace, of two operators XI.6.17 (1026) Transfinite closure of a manifold (462) Transformation see also "Operator" Transformation, measure preserving (687) Transformation, metrically transitive (667) Translate of a function, definition (283) Translation by a vector (36) Translation number IV.7.2 (282) Tseng, Y.Y. 94 Tsuji, M. 338 927 Tukey, J.W. 460—461 Tulajkov, A. 388 Tychonoff theorem, on fixed points V.10.5 (456) (470) Tychonoff theorem, on product spaces I.8.5 (82) Tychonoff, A. 32 372 456 470 Udin, A.I. 396 Ulam, S. 91 1152 Ultrafilter, definition I.7.10 (30) Ultrafilter, properties I.7.11—12 (3O) Unbounded operators, exercises on VII.10 Unbounded operators, in Hilbert space XII Unbounded operators, remarks on (612) Unbounded operators, study of VII.9 Unconditional convergence of a series (92) Uniform boundedness principle, discussion of (30—82) Uniform boundedness principle, for measures IV.9.8 (309) Uniform boundedness principle, in B-spaces II.3.20—21 (66) Uniform boundedness principle, in F-spaces II.1.11 (52) Uniform continuity, criterion for I.6.18 (24) Uniform continuity, definition I.6.16 (23) Uniform continuity, extension of a function I.6.17 (23) Uniform continuity, of an almost periodic function IV.7.4 (283) Uniform convergence, III.6.2—3 (145) III.6.12 Uniform convergence, III.6.1 (145) Uniform convergence, as a criterion for limit interchange I.7.6 (28) Uniform convergence, definition I.7.1 (26) Uniform convergence, remarks concerning (382—383) Uniform convexity, definition II.4.27 (74) Uniform convexity, properties II.4.28—29 (74) Uniform convexity, remarks on (471—474) Uniform countable additivity see "Countably additive" Uniform ergodic theory VIII.8 Uniform ergodic theory, remarks on (730) Uniform operator topology, definition VI.1.1 (475) Uniform operator topology, properties VI.9.11—12 (512—513) Unit sphere in a normed space, compactness and finite dimensionality of IV.3.5 (245) Unit sphere in a normed space, definition II.3.1 (59) Unit, adjunction of in a B-algebra IX.1 (860) Unit, of a group (34) Unitary equivalence of operators X.5.12 (919) Unitary operator X.4.1 (906) Upper bound for an operator XII.5.1 (1240) Urysohn theorems, for normal spaces I.5.2 (15) Urysohn theorems, metrization I.6.19 (24) Urysohn, P. 15 24 van Dantzig, D. 79 91 van Kampen, E.R. 1160 Variation, of a (131) Variation, of a countably additive set function III.4.7 (128) Variation, of a function III.5.15 (140) see "Total Variation, of a regular set function III.5.12 (137)
Реклама
 |
|
О проекте
|
|
О проекте



 -set
-set -field of
-field of 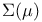
 of
of  -compactness
-compactness  -simple function
-simple function  and
and 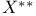 topologies in
topologies in 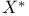
 -uniform convergence, criteria for
-uniform convergence, criteria for