Авторизация
Поиск по указателям
Dunford N., Schwartz J., Bade W.G. — Linear operators. Part 2
Обсудите книгу на научном форуме Нашли опечатку?
Название: Linear operators. Part 2Авторы: Dunford N., Schwartz J., Bade W.G.Аннотация: In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping V ↦ W between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication. An important special case is when V = W, in which case the map is called a linear operator, or an endomorphism of V. Sometimes the definition of a linear function coincides with that of a linear map, while in analytic geometry it does not.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1963Количество страниц: 986Добавлена в каталог: 18.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Masani, P.R. 233 Maslow, A. 233 Matrix (44) Matrix, characteristic polynomial of VII.2.1—4 (561—562) Matrix, exercises on VII.2 Matrix, hermitian (561) Matrix, Jordan canonical form for VII.2.17 (563) Matrix, normal VII.2.14 (563) Matrix, of a projection VI.9.27 (514) Matrix, study of VII.1 Matrix, trace of VI.9.28 (515) Mautner, F.I. 1269 1634 1708 Maximal element, Hausdorff maximality theorem I.2.6 (6) Maximal element, in a partially ordered space I.2.4 (4) Maximal element, relative to a normal operator X.5.6 (913) Maximal ergodic lemma, discrete case VIII.6.7 (676) Maximal ergodic lemma, k-parameter case VIII.7.11 (697) Maximal ergodic lemma, one-parameter continuous case VIII.7.6 (690) Maximal ergodic lemma, remarks on (729) Maximal ideal, definition and existence in a ring (39) Maximum modulus theorem (230—231) Maxwell, J.C. 1749 Mazur theorem, on the convex hull or a compact set V.2.6 (416) Mazur, S. 80 81—82 88 91—92 392 400 416 460 461—462 466 472 883 McShane, E.J. 84 232—233 382 387 927 Mean ergodic theorem (728—729) Mean ergodic theorem, continuous case in VIII.7.4 (689) Mean ergodic theorem, continuous case in VIII.7.10 (694) Mean ergodic theorem, continuous case in B-space VIII.7.1—3 (687—689) Mean ergodic theorem, discrete case in VIII.5.5 (662) Mean ergodic theorem, discrete case in VIII.5.9 (667) Mean ergodic theorem, discrete case in B-space VIII.5.1—4 (661—662) Mean Fubini — Jessen theorem III.11.24 (207) Measurable function, conditions for (total) measurability III.2.21 (116) III.6.9—11 III.6.14 III.9.9 III.9.11 III.9.18 III.9.24 III.6.37 III.9.44 III.13.11 Measurable function, definition III.2.10 (106) Measurable function, extensions of the notion of measurability (118—119) (322) Measurable function, properties III.2.11—12 (106) Measurable function, space of (totally), IV.2.12 (240) (891) Measurable function, space of (totally), as a topological linear space III.9.7 (169) III.9.28 Measurable function, space of (totally), criterion for completeness III.6.5 (146) Measurable function, space of (totally), definition III.2.10 (106) IV.2.27 Measurable function, space of (totally), properties III.2.11—12 (106) Measurable function, space of (totally), remarks concerning (392) Measurable function, space of (totally), study of TM IV.11 IV.15 Measurable set, definition III.4.3 (126) Measure see also "Set function" Measure space, III.5.7 (136) Measure space, as a metric space III.7.1 (158) III.9.6 Measure space, decomposition of see also "Decomposition" Measure space, definition III.4.3 (126) Measure space, finite III.4.3 (126) Measure space, Lebesgue extension of III.5.18 (143) Measure space, positive III.4.3 (126) Measure space, product, of finite number of (188) Measure space, product, of finite number of finite measure spaces III.11.3 (186) Measure space, product, of infinite number of finite measure spaces III.11.21 (205) Measure, Borel or Borel — Lebesgue (189) Measure, Borel — Stieltjes (142) Measure, Borel — Stieltjes, decomposition of see "Decomposition" Measure, Borel — Stieltjes, determined by a function (142) (144) Measure, Borel — Stieltjes, differentiation of III.12 Measure, change of III.10.8 (182) X.I Measure, definition III.4.8 (126) Measure, Haar V.11.22—23 (460) Measure, Hausdorff III.9.47 (174) Measure, invariant VI.9.38—44 (516) Measure, Lebesgue and Lebesgue — Stieltjes (143) Measure, Lebesgue extension of III.5.18 (143) Measure, of hypersurface of unit sphere in XI.7 (1048—1049) Measure, outer III.5.3 (133) Measure, positive matrix XIII.5.12 (1349) Measure, product III.11 Measure, Radon (142) Measure, regular vector-valued IV.13.75 (350) Measure, restriction of (166) Measure, spaces of III.7 IV.2.15—17 IV.9 IV.15 (388—391) Measure, vector-valued, study of IV.10 (301) Measure-preserving transformation (667) Medvedev, Yu.T. 392 Mercer, T. 1088 Mertens, F. 77 Metric spaces, complete I.6.5 (19) Metric spaces, definition I.6.1 (18) Metric spaces, properties I.6 Metric(s) I.6.1 (18) Metric(s), invariant, in a group (90—91) Metric(s), invariant, in a linear space II.1.10 (51) Metric(s), topology in normed linear space II.3.1 (59) (419) Metrically transitive transformation (667) Metrizability see also "Metrization" Metrizability, and dimensionality V.7.9 (436) V.7.34—35 Metrizability, and separability V.5.1—2 (426) V.6.3 V.7.15 Metrization, of a measure space III.7.1 (158) Metrization, of a regular space I.6.19 (24) Metrization, of the set of all functions III.2.1 (102) Michael, E. 462 538 Michael, E.A. 886 931 Michal, A.D. 79 92 610 888 Mihlin, C.G. 1181 Mikusinski, J.G. 395 Miller, D.S. 392 724 729 Milman see "Krein — Milman theorem" Milman, D.P. 94 440 463 466 471 473 1587 1591 Milne, W.E. 1592 1614 Mimura, Y. 541 928 Minimax principle X.4 (908) XIII.9.D Minkowski inequality III.3.3 (120) Minkowski inequality, conditions for equality III.9.43 (173) Minkowski Inequality, generalizations of VI.11.13—18 (530—531) Minkowski, H. 120 372 471 Miranda, C. 88 470 Mirkil, H. 1161 Miyadera, I. 727 Mohr, E. 1590 Molcanov, A.M. 1563 1587 1591 Monna, A.F. 233 400 Montroll, E.W. 406 Moore theorem, concerning interchange of limits I.7.6 (28) Moore, E.H. 28 80 608 Moore, R.L. 48 Morse, A.P. 87 235 393 Moser, J. 612 Moses, H.E. 1622 Moskovitz, D. 466 Muentz, C.H. 384 Multiplicative linear functional IV.6.23 (277) see Multiplicity of eigenvalues X.4 (907) Munroe, M.E. 93 232 235 Murray, F.J. 554 884 886 1269 Myers, S.B. 382 397 Nachbin, L. 93 395 397 398 554 Nagata, J. 385 Nagumo, M. 79 94 394 608 609 726 883 Naimark, M.A. 876 883 884 886 932 1149 1180 1260 1261 1270 1274 1587 1588 1589 1590 1591 1593 1596 1597 1607 1608 1609 1610 1611 Nakamura, M. 233 391 395 539 Nakano, H. 80 395 471 927 928 929 1269 1273 1274 Nakayama, T. 927 Nathan, D.S. 726 Natural domain of existence, of an analytic function (230) Natural embedding of a B-space II.3.18 (66) Natural homomorphism onto factor space (38) (39) Neighborhood, I.6.1 (18) Neighborhood, fundamental family of I.4.6 (10) Neighborhood, of a point or set I.4.1 (10) Nemyckii, V. 1587 Neumann, C. 608 1346 1349 Neumark, M. 396 Newburgh, J.D. 612 Newton, R.G. 1626 Nicolescu, M. 388 Niemytsky, V. 470 Nikodym see also "Radon — Nykodym theorem" Nikodym, boundedness theorem IV.9.8 (309) Nikodym, O.M. 93 160 176 181—182 234—235 309 387 390 392 Nikol'skii, V.N. 94 611 Nikovic, I.A. 1163 Nilpotent element (40) Nilpotent, topological nilpotent in B-algebra IX.2.5 (869) Noerfund, N.E. 75 Non-singular linear transformation (45) Norm, differentiability of (471—473) (474) Norm, existence of (91) Norm, in a B-space II.3.1 (59) Norm, in a conjugate space II.3.5 (60) Norm, in an F-space II.1.10 (51) Norm, in Hilbert space IV.2.26 (242) Norm, in special spaces IV.2 Norm, inequalities on VI.11.30—37 (535—536) Norm, of an operator II.3.5 (60) Norm, topology II.3.1 (50) Normal operator, in a finite dimensional space VII.2.14 (563) Normal operator, in Hilbert space X.1 (887) Normal operator, real and imaginary parts of X.4 (906) Normal structure, definition V.11.14 (459) Normal structure, properties V.11.15—18 (459) Normal subgroup (85) Normal topological space, compact Hausdorff space I.5.9 (18) Normal topological space, definition I.5.1 (15) Normal topological space, metric space I.6.3 (19) Normal topological space, properties I.5.2—4 (15—17) Normal topological space, regular space with countable base (24) Normed (normed linear space) see also "B-space" Normed (normed linear space), definition II.3.1 (59) Normed (normed linear space), study of II.3 Nowhere dense I.6.11 (21) Null function see also "Null set" Null function, criterion for III.6.8 (147) Null function, definition III.2.3 (103) Null set see also "Null function" Null set, additional properties of III.9.2 (169) III.9.8 III.9.16 Null set, criterion for III.6.7 (147) Null set, definition III.1.11 (100) O'Neill, B. 474 Ogasawara, T. 395 927 Ohira, K. 894 Ono, T. 88 400 884 Open set, criterion for I.4.2 (10) Open set, definition I.4.1 (10) Operational calculus X.1 (890) Operational calculus, for functions of an infinitesimal generator VIII.2.6 (645) Operational calculus, for unbounded closed operators VII.9.5 (602) Operational calculus, in finite dimensional space VII.1—5 (558) Operational calculus, in general complex B-space VII.3.10 (568) Operational calculus, remarks on (607—609) Operator topologies VI.1 Operator topologies, bounded strong VI.9.9 (512) Operator topologies, bounded weak VI.9.7—10 (512) Operator topologies, continuous linear functionals in VI.1.4 (477) Operator topologies, properties VI.9.1—12 (511—513) Operator topologies, remarks on (538) Operator topologies, strong VI.1.2 (475) Operator topologies, strongest (538) Operator topologies, uniform VI.1.1 (475) Operator topologies, weak VI.1.3 (476) Operator, adjoint of VI.2 Operator, bound of II.3.5 (60) Operator, bounded XII.1 (1185) Operator, closed II.2.3 (57) XII.1 Operator, compact, definition VI.5.1 (485) Operator, compact, study of VI.5 VII.4 Operator, continuity of, discussion (82—83) Operator, continuity of, in B-spaces II.3.4 (59) Operator, continuity of, in F-spaces II.1.14—16 (54) Operator, definition (36) Operator, equality of XII.1 (1185) Operator, extensions of VI.2.5 (478) (554) XII.1 Operator, finite below XIII.7.25 (1455) Operator, functions of see "Calculus" Operator, graph of II.2.3 (57) XII.1 Operator, hermitian IV.13.72 (350) (561) Operator, ideals of (552—553) (611) Operator, identity (37) Operator, in a finite dimensional space (44) Operator, inverse of XII.1.2 (1187) Operator, limits of, in B-spaces II.3.6 (60) Operator, limits of, in F-spaces II.1.17—18 (54—55) Operator, matrix of (44) Operator, non-singular (45) Operator, norm of II.8.5 (60) Operator, normal VII.2.14 (583) IX.3.14 Operator, perturbation of VII.6 Operator, polynomials in VII.1.1 (556) Operator, product of (37) XII.1.1 Operator, projection (37) VI.3.1 Operator, projection, study of VI.3 Operator, quasi-nilpotent VII.5.12 (581) Operator, range of VI.2.8 (470) Operator, range of, with closed range VI.6 Operator, representation of, in VI.8 Operator, representation of, in C VI.7 Operator, representation of, in other spaces (542—552) Operator, resolvent VII.3.1 (566) Operator, resolvent, study of VII.3 Operator, self adjoint IX.3.14 (879) XII.1.7 Operator, spectral radius of VII.3.5 (567) Operator, spectrum of VII.3.I (566) Operator, sum of (37) XII.1.1 Operator, symmetric X.4.1 (906) XII.1.7 Operator, unbounded VII.9 XII Operator, unbounded, adjoint of XII.1.4 (1188) Operator, unbounded, spectrum and resolvent set of XII.1 (1187) Operator, weakly compact, definition VI.4.1 (482) Operator, weakly compact, study of VI.4 Operator, zero (37) Order of a pole (230) Order of a zero (230) Order of an operator VII.3.15 (57) Ordered representation, definition X.5.9 (916) XII.3.15 Ordered representation, equivalence of X.5.9 (916) XII.3.15 Ordered representation, measure of X.5.9 (916) XII.3.15 Ordered representation, multiplicity of X.5.9 (916) XII.3.15 Ordered representation, multiplicity sets of X.5.9 (916) XII.3.15 Ordered set, definition I.2.2 (4) Ordered set, directed set I.7.1 (26) Ordered set, partially I.2.1 (4) Ordered set, study of I.2 Ordered set, totally I.2.2 (4) Ordered set, well I.2.8 (7) Orientation, of a closed curve (225) Origin, of a linear space II.3.I (59) Orihara, M. 395 Orlicz, W. 80 81—82 83 93 94 235 387 388 391—392 400 543 Orthocomplement of a set in Hilbert space, definition IV.4.3 (249) Orthocomplement of a set in Hilbert space, properties IV.4.4 (249) IV.4.18 Orthogonal complement of a set in a normed space II.4.17 (72) Orthogonal complement of a set in a normed space, remarks on (93) Orthogonal elements and manifolds in Hilbert space IV.4.3 (249) Orthogonal projections in Hilbert spaces IV.4.8 (250) Orthogonal series, exercises on VI.11.43—47 (537) Orthogonal series, study of IV.14 Orthonormal basis in Hilbert space IV.4.11 (252) Orthonormal basis in Hilbert space, cardinality of, IV 4.14 (253) Orthonormal basis in Hilbert space, criteria for IV.4.13 (253) Orthonormal basis in Hilbert space, existence of IV.4.12 (252) Orthonormal set in Hilbert space, closed set IV.14.1 (357) Orthonormal set in Hilbert space, complete set IV.4.8 (250) Orthonormal set in Hilbert space, definition IV.4.3 (250) Orthonormal set in Hilbert space, properties IV.4.9—16 (251—254) Outer measure III.5.8 (133) Owchar, M. 406
Реклама
 |
|
О проекте
|
|
О проекте



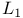
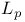
 -measurable function
-measurable function  -finite
-finite  -
- 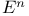
 -, in a metric space
-, in a metric space 