Авторизация
Поиск по указателям
Dunford N., Schwartz J., Bade W.G. — Linear operators. Part 2
Обсудите книгу на научном форуме Нашли опечатку?
Название: Linear operators. Part 2Авторы: Dunford N., Schwartz J., Bade W.G.Аннотация: In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping V ↦ W between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication. An important special case is when V = W, in which case the map is called a linear operator, or an endomorphism of V. Sometimes the definition of a linear function coincides with that of a linear map, while in analytic geometry it does not.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1963Количество страниц: 986Добавлена в каталог: 18.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Dominated ergodic theorem, k-parameter discrete case VIII.6.9 (679) Dominated ergodic theorem, one-parameter continuous case VIII.7.7 (698) Dominated ergodic theorem, one-parameter discrete case VIII.6.8 (678) Dominated ergodic theorem, remarks on (729) Doob, J.L. 729—730 927 929 Dorodnicyn, A.A. 1587 Double norm, definition XI.6.1 (1010) Dual group, definition XI.3.13 (968) Dual space (or conjugate space), definition II.3.7 (61) Dubrovskii, V.M. 389 Duffin, R.J. 1265 Dugundji, J. 470 Dunford, N. 82 84 93 232 235 384 387 389 392 462 540—541 543 554 606 609 612 724 727 729—730 927 Dunham, J.L.. 1592 Dvoretsky, A. 83 Eachus, J.J. 1265 Eberlein — Smulian theorem on weak compactness V.6.1 (430) Eberlein — Smulian theorem on weak compactness, remarks on (466) Eberlein, W.F. 88 386 430 463 466 729 927 1273 Edwards, R.E. 381 884 Egoroff theorem, on almost everywhere and III.6.12 (149) Egoroff, D.T. 149 Eidelheit, M. 91 460 Eigenvalue, definition VII.1.2 (556) VII.11 X.8.1 Eigenvector, definition VII.1.2 (556) X.3.1 Eilenberg, S. 385 397 Elconin, V. 92 Ellis, D. 394 Ellis, H.W. 400 Embedding, natural, of a B-space into its second conjugate II.3.18 (66) End point of an interval III.5.15 (140) End point of an interval, fixed XIII.1 (1279) End point of an interval, free XIII.1 (1279) Entire function, definition (231) Entire function, Liouville's theorem on (231) Equicontinuity, and compactness IV.5.6 (260) IV.6.7—9 Equicontinuity, definition IV.6.6 (268) Equicontinuity, principle of II.1.11 (52) Equicontinuity, quasi-equicontinuity, and compactness IV.6.14 (269) IV.6.29 Equicontinuity, quasi-equicontinuity, definition IV.6.13 (269) IV.6.28 Equicontinuons family of linear transformations, definition V.10.7 (456) Equicontinuons family of linear transformations, fixed point of V.10.8 (457) Equivalence of normed linear spaces, definition II.3.17 (65) Equivalence, *-equivalence of B*-algebras IX.3.4 (875) Erdoes, P. 384 407 Ergodic theorems VII.7 VII.8.8—10 VIII.4—8 see "Maximal "Mean "Pointwise "Uniform Ergodic theorems, remarks on (728—730) Esclangon, E. 1591 Essential least upper bound, definition III.1.11 (100—101) Essential singularity, definition (229) Essential spectrum of a dosed operator XIII.6.1 (1393) Essential supremum, definition III.1.11 (100—101) Essentially bounded, definition III.1.11 (100—101) Essentially bounded, E- X.2 (899) Essentially separably valued, definition III.1.11 (100—101) Esser, M. 927 Euclidean space, definition IV.2.1 (238) Euclidean space, further properties IV.15 (374) Euclidean space, study of IV.3 Euler — Gauss, hypergeometric equation of XIII.8 (1509) Euler, L. 1509 1510 1582 Extended real and complex numbers, definitions (3) Extended real and complex numbers, topology of (11) Extension of a function, by continuity I.6.17 (23) Extension of a function, definition (3) Extension of a function, Tietze's theorem I.5.3—4 (15—17) Extension of measures, Lebesgue III.5.17—18 (142—143) Extension of measures, to a III.5 Extension of measures, to arbitrary sets III.1.9—10 (99—100) Extensions of linear operators VI.2.5 (478) (554) Extremal point and subset, definitions V.8.1 (439) Extremal point and subset, examples and properties V.11.1—6 (457—458) Extremal point and subset, remarks on (466) (473) Extremal point and subset, study of V.8 Extremally disconnected (398) Ezrohi, I.A. 543 F-space basic properties II.1—2 F-space definition II.1.10 (51) F-space examples of IV.2.27—28 (243) Factor group, definition (85) Factor sequence (366) Factor space, in F- and B-spaces, definition II.4.13 (71) Factor space, in F- and B-spaces, properties II.4.13—20 (71—72) Factor space, in F- and B-spaces, remarks on (88) Factor space, in vector spaces (38) Fagan, R.E. 406 Fage, M.K. 1587 1589 Fan, K. 395 397 610 Fantappie, L. 399 607 Farnell, A.B. 1163 Fatou theorem, on limits and integrals III.6.19 (152) III.9.35 Fatou, P. 152 Fell, J.M.G. 927 Feller, W. 727 1589 1628 Fenchel, W. 471 Feynman, R.P. 406 Fichtenholz, G. 83 233 373 386 388 543 Ficken, F.A. 393 394 Field, III.4.2 (126) III.5.6 Field, definition III.1.3 (96) Field, determined by a collection of sets III.5.6 (135) Field, in algebraic sense (33) Field, Lebesgue extension of a III.5.18 (143) Field, of subsets of a set, Bord field III.5.10 (137) Field, restriction of a set function to (166) Filter, definition and properties I.7.10—12 (30—31) Finite dimensional function on a group, definition XI.1.3 (940) Finite dimensional spaces, additional properties IV.15 (374) Finite dimensional spaces, definitions IV.2.1—3 (238—239) Finite dimensional spaces, study of IV.3 Finite intersection property, as criterion for compactness I.5.6 (17) Finite intersection property, definition I.5.5 (17) Finite measure(space), III.5.7 (136) see "Measure Finite measure(space), criterion for and properties III.4.4—9 (127—129) Finite measure(space), definition III.4.3 (126) Finite measure(space), Saks decomposition of IV.9.7 (308) Finitely additive set function see also "Set function" Finitely additive set function, definition III.1.2 (96) Finitely additive set function, study of III.1—3 Fischer, C.A. 380 539 543 Fischer, E. 373 Fixed point property, definition V.10.1 (453) Fixed point property, exercises V.11.17—23 (459—460) Fixed point property, remarks on (467—470) (474) Fixed point property, theorems V.10 Fleischer, I. 88 400 Foias, C. 1267 1268 Folner, E. 399 Fort, M.K. 471 Fortet, R. 93 406 473 Fourier coefficients, definition IV.14.12 (358) Fourier series, convergence of IV.14.27 (360) IV.14.29—33 Fourier series, definition IV.14.12 (358) Fourier series, localization of IV.14.26 (360) Fourier series, multiple series IV.14.68 (367) Fourier series, multiple series, study of, IV.14.69-73 (367—368) Fourier series, study of IV. 14 IV.14.12—20 Fourier sine and cosine theorems XIII.5 (1388) Fourier, J.B.J. 1388 Frechet differential, definition (92) Frechet differential, theory for compact operators VII.4 Frechet, M. 79 233 373 380 382 387—888 398 780 Fredholm alternative (609—610) Fredholm, I. 79 609 1085 Freudenthal, H. 84 394 395 1273 Friedrichs, K.O. 401 405 407 612 927 1184 1240 1273 1501 1545 1546 1585 1586 1591 1592 1604 1635 1748 1749 Frink, O. 94 Frobenius, G. 607 1080 1147 Fubini theorem, for general finite measure spaces III.11.18 (193) Fubini theorem, for positive III.11.9 (190) Fubini — Jessen theorems, mean III.11.24 (207) Fubini — Jessen theorems, pointwise III.11.27 (209) Fubini, G. 190 207 209 Fuchs, L. 1588 Fuglede, B. 934 Fukamiya, M. 466 729 884 Fullerton, R.E. 396 397 540 543 552 Function, absolutely continuous IV.2.22 (242) Function, Additive set see "Set function" Function, almost periodic IV.2.25 (242) IV.7 Function, analytic III.14 Function, analytic, between complex vector spaces VI.10.5 (522) Function, Borel — Stieltjes measure of III.5.17 (142) Function, characteristic (8) Function, continuous I.4.15 (13) Function, convex VI.10.1 (520) Function, definition (3) Function, domain of (2—3) Function, entire (231) Function, essential bound or supremum of III.1.11 (100) Function, extension of (3) Function, homeomorphism I.4.15 (13) Function, homomorphism (35) (39) (40) (44) Function, integrate III.2.17 (112) IV.10.7 Function, inverse (3) Function, isometry II.3.17 (65) Function, isomorphism (85) (88) (39) Function, linear functional (38) Function, linear operator (86) Function, measurable III.1.10 (106) III.2.22 (323) Function, metric I.6.1 (18) Function, null III.2.3 (103) Function, of an operator see "Calculus" Function, of bounded variation III.5.15 (140) Function, one-to-one (3) Function, operator (36) Function, orthonormal system of IV.14.1 (357) Function, projection I.3.14 (9) (37) IV.4.8 Function, range of (3) Function, representation of vector valued III.11.15 (194) Function, resolvent VII.3.1 (566) Function, restriction of (3) Function, set III.1.1 (95) Function, simple III.2.9 (105) (322) Function, subadditive (618) Function, support V.1.7 (410) Function, tangent V.9.2 (446) Function, total variation of III.5.15 (140) Function, totally measurable III.2.10 (106) see Function, uniformly continuous I.6.16 (28) Functional(s), bilinear II.4.4 (70) Functional(s), continuous II.3.7 (61) Functional(s), continuous, existence of II.3.12—14 (64—65) Functional(s), continuous, extension of II.3.10—11 (62—63) Functional(s), continuous, for representation in special spaces IV.15 Functional(s), continuous, non-existence of (329—330) (892) Functional(s), discontinuous, existence of I.3.7 (8) Functional(s), in bounded V.5.6 (428) Functional(s), in weak and strong operator topologies VI.1.4 (477) Functional(s), linear (38) Functional(s), multiplicative IV.6.23 (277) Functional(s), multiplicative, in the unit sphere of C* V.3.6 (441) Functional(s), multiplicative, of V.8.9 (443) Functional(s), separating V.1.9 (411) Functional(s), tangent, V-9.4 (447) Functional(s), total space of V.8.1 (418) Functions, of an element in a B*-algebra IX.3.12 (878) Functions, special XIII.9.1 (1569) Fundamental family of neighborhoods, definition I.4.6 (10—11) Fundamental set, in a linear topological space II.1.4 (50) Gagaev, B. 93 Gal, I.S. 80 82 Gale, D. 382 Gantmacher, V. 463 485 539 Garabedian, P.R. 88 Garding, L. 1269 1634 1708 1716 Gauss, C.F. 1509 Gavurin, M.K. 612 Gelbaum, B.R. 64 Gelfand — Neumark theorem IX.3.7 (876) Gelfand, I.M. 79 94 232 235 347 384 385 396 407 589 540 543 608 609 876 888 884 1149 1160 1587 1616 1622 1628 1624 1625 Generalized sequence, definition and properties I.7.1—7 (26—29) Generator, infinitesimal of a semigroup of operators VIII.1.6 (619) Gibbs, J.W. 657 Gillespie, D.C. 462 Giorgi, G. 607 Glazman, I.M. 926 927 929 1269 1270 1272 1273 1274 1587 1588 1589 1590 1591 1592 1599 Glicksberg, I. 381 Glivenko, V. 391 Godement, R. 930 1160 1274 Goedel, K. 47—48 Gohberg, I.C. 610 611 1163 Gol'dman, M.A. 611 Goldstine, H.H. 81 424 463 Gomes, A.P. 399 Goodner, D.B. 398 554 Gowurin, M. 233 391 543 552 Graph, closed graph theorem II.2.4 (57) Graph, of an operator II.2.8 (57) Graves, L.M. 48 85 92 232 235 383 391 467 611 Graves, R.F. 406 Graves, R.L. 610 Green's formula XIII.2.4 (1288) Green, G. 1288 Grimshaw, M.E. 606 Grinblyum, M.M. 94 Grosbeig, Y. 392 Grosberg, J. 395 Grothendieck, A. 9O 383 389 398 399 466 540 543 552 553 610 Group, basic properties I.10 Group, definition (84) Group, metrizable (90) Group, representations (1145—1149) Group, topological II.1.1 (49) Gurevic, L.A. 94 Haar measure on a compact group V.11.22—28 (460) XI.1.1 Haar measure on a compact group, definition XI.1.2 (940) Haar measure on a compact group, in a locally compact group XI.8 (950) Haar measure on a compact group, in a locally compact group, properties of XI.11 (1150—1155) Haar, A. 927 1147 1152 1583 1616 1617 Hadamard three circles theorem VI.11.48 (538) Hadamard's inequality XI.6.12 (1018) Hadamard, J. 380 538 1018 Hahn decomposition theorem III.4.10 (129) Hahn extension theorem III.5.8 (136) Hahn — Banach theorem II.3.10 (62) Hahn — Banach theorem, discussion of (85—88) Hahn, H. 48 62 80 85 86 88 129 133 158 232 233 234—235 390 539 928 1269 Halberg, C.J.A., Jr. 1087 Halmos, P.R. 48 80 232 235 381 389 390 606 608 722 728 729 926 927 928 929 931 932 933 934 1152 1269 Halperin, I. 400 473 1586 1588 1591 Hamburger moment problem XII.8.1 (1251) Hamburger, H.L. 606 611 1250 1251 Hamel base or basis, definition (36) Hamel base or basis, for general vector spaces I.14.2 (46) Hamel base or basis, for real numbers I.3.7 (8) Hankel transform XI.8.23 (978) (1535) Hankel, H. 1348 1349 1535 Hanson, E.H. 392 Harazov, D.F. 611 Hardy — Hilbert type inequalities VI.11.19—29 (531—584) Hardy, G.H. 78 864 531—533 538 541 713 1004 1006 1007 1076 1183 1184 1591 Hartman, P. 399 729 1551 1553 1555 1556 1558 1559 1560 1561 1562 1585 1587 1590 1591 1592 1596 1597 1598 1599 1600 1601 1602 1603 1605 1606 1607 1614 1615 1616 1626 Hatfield, C. 406 Hausdorff III.9.47 (174) Hausdorff maximality theorem I.2.6 (6) Hausdorff space, criterion for I.7.3 (27) Hausdorff space, definition I.5.1 (15) Hausdorff, F. 6 47—48 79 89 174 380 529 539 1250 Heaviside, O. 1648
Реклама
 |
|
О проекте
|
|
О проекте



 -uniform convergence
-uniform convergence  -field
-field  topology
topology 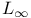
 -measure
-measure