Авторизация
Поиск по указателям
Dunford N., Schwartz J., Bade W.G. — Linear operators. Part 2
Обсудите книгу на научном форуме Нашли опечатку?
Название: Linear operators. Part 2Авторы: Dunford N., Schwartz J., Bade W.G.Аннотация: In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping V ↦ W between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication. An important special case is when V = W, in which case the map is called a linear operator, or an endomorphism of V. Sometimes the definition of a linear function coincides with that of a linear map, while in analytic geometry it does not.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1963Количество страниц: 986Добавлена в каталог: 18.02.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
XI.3.2 (953) III.9.29 (171) III.9.29—31 (171) (394—396) III.6.6 (146) III.9.10 III.3.6—7 (122—124) III.6.15 IV.15 III.4.4 (121) (387—388) III.8.5 (168) III.9.6 III.3 III.6 IV.8 IV.15 IV.2.19 (244) IV.8 IV.15 a.e. see "Almost everywhere" Abdelhay, J. 397 Abel summability, of series II.4.42 (76) Abel, N.H. 76 352 383 Abelian group (34) Absolute convergence, in a B-space (93) Absolutely continuous functions, definition IV.2.22 (242) Absolutely continuous functions, set function see "Continuous set function" "Set Absolutely continuous functions, space of, additional properties IV.15 (378) Absolutely continuous functions, space of, definition IV.2.22 (242) Absolutely continuous functions, space of, remarks concerning (392) Absolutely continuous functions, space of, study of IV.12.8 (338) Accumulation, point of I.4.1 (10) Adams, C.R. 393 Additive set function see "Set function" Adjoint element, in an algebra with involution (40) see Adjoint of an operator, between B-spaces VI.2 Adjoint of an operator, compact operator VI.5.2 (485) VI.5.6 VII.4.2 Adjoint of an operator, continuity of operation VI.9.12 (513) Adjoint of an operator, criterion for VI.9.13—14 (513) Adjoint of an operator, in Hilbert space VI.2.9 (479) VI.2.10 Adjoint of an operator, remarks on (538) Adjoint of an operator, resolvent of VII.3.7 (568) Adjoint of an operator, spectra of VII.3.7 (568) VII.5.9—10 VII.5.23 Adjoint of an operator, weakly compact operator VI.4.7—8 (484—485) Adjoint space, definition II.3.7 (61) Adjoint space, representation for special spaces IV.15 Affine mapping, definition (456) Affine mapping, fixed points of V.10.6 (456) Agmon, S. 1161 Agnew, R.P. 87 Ahiezer, N.I. 936 927 929 1269 1270 1272 1273 1274 1276 1588 1589 1590 1592 Ahlfors, L.V. 48 Akilov, G.P. 554 Alaoglu, L. 235 424 462 463 729 Alexandroff theorem, on C(S) convergence of bounded additive set functions IV.9.15 (316) Alexandroff theorem, on countable additivity of regular set functions on compact spaces III.5.13 (138) Alexandroff, A.D. 138 233 316 380—381 390 Alexandroff, P. 47 467 Alexiewicz, A. 82 83 234 235 392 543 Algebra, algebraic preliminaries I.10—13 Algebra, B*-algebra IX.3 Algebra, B*-algebra, *-equivalences of B*-algebras IX.3.4 (875) Algebra, B*-algebra, *-homomorphism in IX.3.4 (875) Algebra, B*-algebra, *-isomorphism of IX.3.4 (875) Algebra, B*-algebra, as an algebra of continuous functions IX.3.7 (876) Algebra, B*-algebra, non-commutative IX.5 (884—886) Algebra, B*-algebra, spectrum of IX.3.4 (875) Algebra, B-algebra IX Algebra, B-algebra, as an algebra of continuous functions IX.2.9 (870) Algebra, B-algebra, as an operator algebra IX.1 (860) Algebra, B-algebra, generating set for IX.2.10 (870—871) Algebra, B-algebra, ideal in IX.1 (865—866) Algebra, B-algebra, quotient IX.1 (866) Algebra, B-algebra, radical of IX.2.5 (869) Algebra, B-algebra, semi-simple IX.2.5 (869) Algebra, B-algebra, structure space of (869) Algebra, boolean see also "Field of sets" Algebra, Boolean, definition (43) Algebra, Boolean, representation of (44) Algebra, commutative IX.1.1 (860) IX.2 Algebra, definition (40) Algebra, of sets see "Field of sets" Algebra, quotient (40) Almost everywhere (or III.1.11 (100) Almost everywhere (or IV.10.6 (322) Almost periodic functions, definition IV.2.25 (242) Almost periodic functions, space of, additional properties IV.15 (379) Almost periodic functions, space of, definition IV.2.25 (242) Almost periodic functions, space of, remarks concerning (386—387) Almost periodic functions, space of, study of IV.7 Almost uniform (or III.6.1 (145) see Altman, M.S. 94 609 610 Ambrose, W. 1013 1160 1274 Analytic continuation (230) Analytic function (vector-valued), between complex vector spaces VI.10.5 (522) Analytic function (vector-valued), definition (224) Analytic function (vector-valued), properties III.14 Analytic function (vector-valued), space of, definition IV.2.24 (242) Analytic function (vector-valued), space of, properties, IV 15 Annihilator of a set II.4.17 (72) Anzai, H. 886 Arens' lemma IX.3.5 (875—876) Arens, R.F. 381 382 384 385 396—397 399 466 875 884 886 Arnous, E. 1274 Aronszajn, N. 87 91 234 394 610 928 980 1120 Artemenko, A. 387 392 Arzela theorem, on continuity of limit function IV.6.11 (268) Arzela theorem, on continuity of limit function, remarks concerning (383) Arzela, C. 266 268 382 383 Ascoli — Arzela theorem, on compactness of continuous functions IV.6.7 (266) Ascoli — Arzela theorem, remarks concerning (382) Ascoli, G. 266 382 460 466 Atkinson, F.V. 610 611 1615 Atom, in a measure space IV.9.6 (308) Audin, M. 611 Automorphisms, in groups (35) B*-algebras IX.3 (874—879) see B-algebra see "Algebra" B-space (or Banach space), basic properties of II B-space (or Banach space), definition II.3.2 (59) B-space (or Banach space), integration III B-space (or Banach space), special B-spaces IV B-space (or Banach space), special B-spaces, properties IV.15 Babenko, K.I. 94 1183 Bade, W.G. 538 612 728 928 1269 Baire category theorem I.6.8 (20) Baire, R. 20 Baker, H.F. 1588 Banach limits, existence and properties II.4.22—23 (73) Banach theorem, on convergence of measurable functions IV.11.2—3 (332—334) Banach — Stone theorem, on equivalence of C-spaces V.8.8 (442) Banach — Stone theorem, on equivalence of C-spaces, remarks on (396—397 466) Banach, S. 59 62 73 80 81 82—84 85 86 89 91—93 94 234 232 380 385—386 392 442 462—463 465—466 472 538 539 609 Barankin, E.W. 1163 Bari, N.K. 94 Bartle, R.G. 85 92 233 383 386 389 392 539—540 543 Base (or basis) see also "Hamel base" Base (or basis), in a B-space, criterion for compactness with IV.5.5 (260) Base (or basis), in a B-space, definition II.4.7 (71) Base (or basis), in a B-space, properties II.4.8—12 (71) Base (or basis), in a B-space, remarks on (93—94) Base (or basis), in a linear space see "Hamel base" Base (or basis), orthogonal and orthonormal bases in Hilbert space, definition IV.4.11 (252) Base (or basis), orthogonal and orthonormal bases in Hilbert space, existence of IV.4.12 (252) Base for a topology, criterion for I.4.7 (11) Base for a topology, definition I.4.6 (10) Base for a topology, theorems concerning countable bases I.4.14 (12) I.6.12 I.6.19 Basic separation theorem concerning convex sets V.1.12 (412) Bellman, R. 1550 Bendixon, I. 1080 Bennett, A.A. 85 Berezanskii, Yu.M. 1587 1626 Berkowitz, J. 1543 1580 1591 1592 1594 1595 1599 1604 Bernoulli, D. 1581 1582 Bernstein theorem, concerning cardinal numbers I.14.2 (46) Bernstein, F. 46 Berri, R. 395 Besicovitch, A.S. 386 Bessel equation XIII.8 (1535) Bessel, F.W. 977 1348 1349 1535 Beurling, A. 361 930 978 1100 1161 1162 Bieberbach, L. 48 Bilateral Laplace and Laplace — Stieltjes transforms, definitions VIII.2.1 (642) Bilinear functional II.4.4 (70) Biorthogonal system, in a B-space II.4.11 (71) Birkhoff, G. 48 90 93 232 235 393—394 395 729 Birkhoff, G.D. 470 658—658 729 1497 1583 1586 1589 1592 Birnbaum, Z.W. 400 Blumenthal, L.M. 393 Boas, R.P., Jr. 94 473 1266 Bocher, M. 1583 1588 1589 Bochner moment problem XII.8.3 (1254) Bochner, S. 232—233 235 283 315 386 390 395 540 543 552 883 1160 1254 1273 1274 Bodiou, G. 1264 Bogoliouboff, N. 730 Bohnenblust, H.F. 86 94 393 394 395—396 554 Bohr, H. 281 386—387 399 949 1149 Bohr, H., theorem concerning almost periodic functions XI.2.4 (949) Boltzmann, L. 657 Bonnesen, T. 471 Bonsall, F.F. 88 Boolean algebra see also "Boolean ring" Boolean algebra, definition (43) Boolean algebra, properties (44) Boolean algebra, representation of (441 Boolean ring, definition (40) Boolean ring, representation of I.12.1 (41) Borel field of sets, definition III.5.10 (187) Borel function X.1 (891) Borel measurable function X.1 (891) Borel measure (or Borel — Lebesgue measure), construction of (139) III.13.8 Borel — Stieltjes measure (142) Borel, E. 132 139 142 1588 Borg, G. 1501 1622 Borsuk, K. 91 Botts, T. 387 460 Bound, of an operator II.8.5 (60) Bound, of an operator, in a partially ordered set I.2.3 (4) Bound, of an operator, in the (extended) real number system (3) Boundary condition, adjoint XII.4.27 (1237) Boundary condition, definition XII.4.25 (1285) see boundary Boundary condition, linearly independent XII.4.25 (1235) Boundary condition, symmetric XII.4.25 (1286) Boundary values, complete set of XII.4.22 (1235) see Boundary values, for an operator XII.4.20 (1284) Boundary, of a set I.4.9 (11) Bounded V.5.6 (428) Bounded V.5.4 (427) Bounded function space, additional properties IV.15 Bounded function space, definition IV.2.13 (240) Bounded function space, remarks concerning (373) Bounded function space, study of IV.5 Bounded sets, in linear spaces V.7.5 (436) V.7.7 V.7.8 Bounded strong operator topology, definition and properties VI.9.9 (512) Bounded variation of a function, additional properties IV.15 (378) Bounded variation of a function, criterion to be IV.13.73 (350) Bounded variation of a function, definition III.5.15 (140) Bounded variation of a function, generating Borel — Stieltjes measure (142) Bounded variation of a function, integral with respect to IV.13.63 (349) Bounded variation of a function, integration by parts III.6.22 (154) Bounded variation of a function, remarks on (392—393) Bounded variation of a function, right- and left-hand limits of III.5.16 (140) III.6.21 Bounded variation of a function, set function, criteria for III.4.4—5 (127—128) see Bounded variation of a function, set function, definition III.1.4 (97) Bounded variation of a function, study of IV.12 Bounded weak operator topology, definition and properties VI.9.7—10 (512) Bounded, essentially (or III.1.11 (101) Bounded, operator, definition II.3.5 (60) Bounded, set in a linear topological space II.1.7 (51) Bounded, set in a linear topological space, criterion for boundedness in a B-space II.3.3 (59) Bounded, set in a linear topological space, remarks on (80) Bounded, totally bounded set, definition I.6.14 (22) Boundedness, in F-spaces II.1.11 (52) Boundedness, of a continuous function on a compact set I.5.10 (18) Boundedness, of a finite countably additive set function III.4.4—7 (127—128) Boundedness, of an almost periodic function IV.7.3 (283) Boundedness, principle of uniform boundedness in B-spaces II.3.20—21 (66) (80—82) Bounding point of a set, criteria for V.1.8 (411) V.2.1 Bounding point of a set, definition V.1.6 (410) Bourbaki, N. 47 80 62 84 232 382 463 465 471 Bourgin, D.G. 383 462 Brace, J.W. 466 Bram, J. 932 933 Brauer, A. 1078 Brauer, R. 1149 Bray, H.E. 391 Brelot, M. 1268 Brillouin, L. 1592 1614 Brodsku, M.S. 471 1164 Brouwer fixed point theorem, proof of (467) Brouwer fixed point theorem, statement (453) Browder, F.E. 1269 1634 1635 1708 1746 Brown, A. 934 935 Buchheim, A. 697 Buniakowsky, V. 372 Burkhardt, H. 1589 Cafiero, F. 389 392 Calderon — Zygmund inequality XI.7.11 (1063) XI.7.16 Calderon — Zygmund, convolution kernel of XI.7.4 (1058) Calderon — Zygmund, convolution product of XI.7.6 (1054) Calderon, A.P. 541 730 1063 1072 1077 1164 1165 Calkin, J.W. 553 1270 1273 1586 1589 Cameron, R.H. 406 407 Camp, B.H. 390 Canonical factorization of operators XII.7 Cantor diagonal process (23) Cantor perfect set V.2.13—14 (486) Caratheodory theorem, concerning outer measures III.5.4 (134) Caratheodory, C. 48 134 232 729 1048 Cardinal numbers, Bernstein theorem I.14.2 (46) Cardinal numbers, comparability theorem I.3.5 (3) Carleman's inequality XI.6.27 (1038) Carleman, T. 536 627 1162 1163 1268 1260 1277 Cartan, E. 607 1148 Cartan, H. 80 1152 1160 1274 Cartesian product of sets, definition I.3.11 (9) Cartesian product of sets, properties I.3.12—14 (9) Cartesian product of topological spaces I.8 (81) Category theorem, of Baire I.6.9 (20) Cauchy integral formula (227) Cauchy integral formula, for functions of an operator, in a finite dimensional space VII.1.10 (560) Cauchy integral formula, for functions of an operator, in general space VII.8.9 (568) Cauchy integral formula, for unbounded closed operators VII.9.4 (601) Cauchy integral formula, remarks on (607—609) (612) Cauchy integral theorem (225) Cauchy problem (613—614) (639—641) Cauchy sequence, generalized (28) Cauchy sequence, in a metric space I.6.5 (18—20) Cauchy sequence, weak, criterion for in various spaces IV.15 Cauchy sequence, weak, in a B-space II.3.25 (67—68) Cauchy, A. 372 382—383 Cayley, A. 1270 1271 Cech compactification theorem IV.6.22 (276) Cech compactification theorem, of a completely regular space (279) Cech, E. 279 385 872 Cesaro summability, of Fourier series IV.14.44 (363) Cesaro summability, of series II.4.37 (75) Cesaro, E. 75 352 363 Chang, S.H. 610 1168 Change of variables, for functions III.8.4—5 (222—228) Change of variables, for measures III.10.8 (182) Character group, definition XI.3.13 (968) Character, definition XI.1.5 (944) Characteristic function (3) Characteristic polynomial, definition VII.2.1 (561) XI.6.9 Characteristic polynomial, properties VII.2.1—4 (561—562) VII.5.17 VII.10.8 Characteristic value (606)
Реклама
 |
|
О проекте
|
|
О проекте



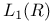 as a B-algebra
as a B-algebra 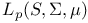 , 0<p<1, definition
, 0<p<1, definition  , characterizations of
, characterizations of 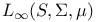 , definition
, definition  -almost everywhere) definition for additive scalar set functions
-almost everywhere) definition for additive scalar set functions  topology, continuous linear functionals
topology, continuous linear functionals