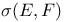Авторизация
Поиск по указателям
Bogachev V.I. — Measure Theory Vol.1
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure Theory Vol.1Автор: Bogachev V.I. Аннотация: Measure theory is a classical area of mathematics born more than two thousand years ago. Nowadays it continues intensive development and has fruitful connections with most other fields of mathematics as well as important applications in physics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2007Количество страниц: 500Добавлена в каталог: 22.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Singular measure 178 Singularity of measures 178 Sinitsyn I.N. 414 Sion M. 414 423 430 Skorohod (Skorokhod) A.V. viii 413 Slutsky E. 171 426 Smiley M.F. 422 Smirnov V.I. 412 426 435 Smital J. 403 Smith H.J.S. 419 Smith H.L. 435 Smulian V.L. 282 434 Sobolev derivative 377 Sobolev inequality 377 378 Sobolev S.L. 325 376 Sobolev space 377 Sobolev V.I. 414 Sodnomov B.S. 87 Sohrab H.H. 414 Solovay R. 80 Soucek J. 379 Souslin M. vii. viii 35 417 420 Souslin operation 36 Souslin scheme 36 Souslin scheme, monotone 36 Souslin scheme, regular 36 Souslin set 39 420 Space of measures 273 Space, 373 Space, 306 Space, Banach 249 Space, Banach, reflexive 281 Space, dual 256 262 281 283 311 313 Space, Euclidean 254 Space, Hilbert 255 Space, Lorentz 320 Space, measurable 4 Space, metric, complete 249 Space, metric, separable 252 Space, normed 249 Space, normed, complete 249 Space, normed, uniformly convex 284 Space, Orlicz 320 Space, probability 10 Space, Sobolev 377 Spiegel M.R. 414 Sprecher D.A. 414 Srinivasan T.P. 94 414 419 420 Staircase of Cantor 193 Stampacchia G. 160 Standard Gaussian measure 198 Steen P. van der 414 Stein E.M. 65 238 320 353 367 374 375 379 386 398 414 430 431 436 Steiner J. 212 Steiner’s symmetrization 212 Steinhaus H. 85 100 102 264 430 431 Stepanoff W. 438 Stieltjes 33 152 Stieltjes T.J. 33 152 416 425 Stolz O. 417 Stone M.H. viii 411 423 Stromberg K. 81 325 402 414 435 Stroock D.W. 414 Structure 277 Structure, 277 Structure, complete 277 Stute W. 413 Subadditivity 9 Subadditivity, countable 11 Sublinear function 67 Submeasure 75 Submeasure, Maharam 75 Submodular set function 75 Subramanian B. 310 Sucheston L. 435 438 Sudakov V.N. 318 434 Suetin P.K. 261 Sullivan D. 422 Sullivan J.A. 413 Sum Fejer 261 Sun Y. 237 Supermodular set function 75 Supremum 277 Surface measure 383 Surface measure on the sphere 238 Svetic R.E. 422 Swanson L.G. 91 Swartz Ch.W. 319 353 413 414 437 Symmetrization of Steiner 212 Sz.-Nagy B. 163 412 414 Szpilrajn E. 80 420 Szymanski W. 416 Table of sets 36 TagamLickii Ya.A. 321 Tagged interval 353 Tagged partition 354 Tagged partition, free 351 Talagrand M. 75 235 Tarski A. 81 422 Taylor A.E. 414 416 432 Taylor J.C. 414 Taylor S.J. 243 414 Teicher H. 413 Telvakovski T S.A. 415 Temple G. 414 Ter Horst H.J. 428 Theodorescu R. 431 Theorem, Baire 166 Theorem, Baire, category 89 Theorem, Banach — Alaoglu 283 Theorem, Banach — Steinhaus 264 Theorem, Banach — Tarski 81 Theorem, Beppo — Levi monotone convergence 130 Theorem, Besicovitch 361 Theorem, Bochner 220 Theorem, Carleson 260 Theorem, covering 361 Theorem, Denjoy — Young — Saks 370 Theorem, Dieudonne viii Theorem, differentiation 351 Theorem, Eberlein — Smulian 282 Theorem, Egoroff 110 426 Theorem, Fatou 131 Theorem, Fichtenholz viii 271 433 Theorem, Fubini 183 185 209 336 409 429 Theorem, Gaposhkin 289 434 Theorem, Grothendieck viii Theorem, Hahn — Banach 67 Theorem, Komlos 290 Theorem, Krein — Milman 282 Theorem, Lebesgue on the Baire classes 149 Theorem, Lebesgue — Vitali 268 Theorem, Lebesgue, dominated convergence 130 Theorem, Lusin 115 426 Theorem, mean value, first 150 Theorem, mean value, second 150 Theorem, Miintz 305 Theorem, monotone class 33 Theorem, monotone class functional 146 Theorem, Nikodym 274 Theorem, Plancherel 237 Theorem, Radon — Nikodym 177 178 180 256 429 Theorem, Riemann — Lebesgue 274 Theorem, Riesz 112 256 262 Theorem, Riesz — Fischer 259 Theorem, Sard 239 Theorem, Scheffe 134 428 Theorem, Sierpiriski 48 421 Theorem, Tonelli 185 Theorem, Ulam 77 Theorem, Vitali on covers 345 Theorem, Vitali — Lebesgue — Hahn — Saks 274 432 Theorem, Vitali — Scheffe 134 Theorem, Young 134 428 Thielman H. 414 Thomson B.S. 210 404 413 421 436 438 Tikhomirov V.M. 420 Titchmarsh E.C. 308 394 401 411 430 431 Tkadlec J. 244 404 Tolstoff (Tolstov. Tolstow) G.P. 159 388 402 407 414 437 Tonelli L. 185 409 423 429 Tonelli theorem 185 Topology of setwise convergence 291 Topology, 281 Topology, density 398 Topology, generated by duality 281 Topology, weak 281 Topology, weak* 283 TopsoeF. 421 438 Toralballa L.V. 414 Torchinsky A. 414 436 Tornier E. 411 Tort rat A. 414 Total variation 220 Total variation of a measure 176 Touzillier L. 414 Townsend E.J. 411 Trace of a 8 Transform, Fourier 197 Transform, Fourier, inverse 200 Transform, Laplace 237 Transform, Radon 227 Transhnite 63 Tricomi F.G. 414 Tumakov I.M. 416 417 423 Two-valued measurable cardinal 79 Tzafriri L. 433 Uhl J.J. 423 Uhrin B. 431 Ulam S. 77 419 422 430 Ulam theorem 77 Ulyanov P.L. 85 413 415 Unbounded measure 24 Uniform, absolute continuity of integrals 267 Uniform, convexity of 284 Uniform, countable additivity 274 Uniform, integrability 267 285 Uniform, integrability, criterion 272 Uniformly convex space 284 Uniformly integrable set 267 Unit of algebra. 4 Upper bound of partially ordered set 277 Ursell H.D. 435 Us G.F. 413 V(f, [a, t]) 332 Vaisala J 382 Vajda I. 154 Vakhania N.N. 169 Valadier M. 299 Vallee Poussin Ch.J. de la see “la Vallee Poussin Ch.J. de” Value, essential 166 van Brunt B. see “Brunt B. van” van Dalen D. see “Dalen D. van” van der Steen P. see “Steen P. van der” van Kampen E.R. see “Kampen E.R. van” van Os C.H. see “Os C.H. van” van Rooij A.CM. see “Rooij A.C.M. van” Van Vleck E.B. 425 Variation of a function 332 Variation of a measure 176 Variation of a set. function 220 Vath M. 414 Vector sum of sets 40 Veress P. 321 426 Verley J.-L. 414 Version of a function 110 Vestrup E.M. 103 229 414 Vinti C. 414 Viola T. 414 Visintin A. 299 Vitali G. v 31 134 149 268 274 345 409 411 414 417 419 426 428 432 433 436 437 Vitali — Lebesgue — Hahn — Saks theorem 274 432 Vitali — Scheffe theorem 134 Vitali, example 31 Vitali, system 397 Vitushkin A.G. 437 Vladimirov D.A. 421 Vo-Khac Kh. 414 Vogel W. 414 Volcic A. 414 Volterra V. 416 425 Volume of the ball 239 Volume, mixed 226 Vol’berg A.L. 375 von Neumann J. see “Neumann J. von” vraisup 140 Vulikh B.Z. 104 414 Vvbornv R. 437 V_a^b(f)$ 332 Wagon S. 81 82 Wagschal C. 414 415 Walter W. 414 Wang Z.Y. 423 Warmiith W. 413 Warmuth E. 413 Wazewski T. 418 Weak, compactness 285 Weak, compactness in 285 Weak, compactness in 282 Weak, convergence 281 Weak, convergence in 282 Weak, topology 281 weakly convergent sequence 281 Weber H. 61 Weber K. 413 422 Weber M. 435 Weierstrass K. 260 416 Weighted inequality 374 Weil A. viii Weir A.J. 414 Weiss G. 238 320 430 431 435 Weiss N.A. 414 415 Well-ordered set 62 Wesler O. 91 Weyl H. 426 Wheeden R.L. 414 Whitney decomposition 82 Whitney H. 82 373 Widom H. 414 Wiener N. 409 417 419 430 Wierdl M. 435 Wilcox H.J. 414 Williams D. 414 Williamson J.H. 414 Willmott R.C. 430 Wintner A. 430 Wise G.L. 81 228 395 414 Wolff J. 419 Wolff T. 66 Wu J.-M. 376 Ye D. 382 Yeh J. 414 Yosida K. 431 Young G.C. 370 409 417 Young inequality 205 Young theorem 134 428 Young W.H. v 93 134 205 316 409 417 418 421 423 425 428 432 434 436 Younovitch B. 438 Zaanen A.C. 310 312 320 414 438 Zabreiko P.P. 157 434
Реклама
 |
|
О проекте
|
|
О проекте



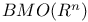

 -complete
-complete