Авторизация
Поиск по указателям
Bogachev V.I. — Measure Theory Vol.1
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure Theory Vol.1Автор: Bogachev V.I. Аннотация: Measure theory is a classical area of mathematics born more than two thousand years ago. Nowadays it continues intensive development and has fruitful connections with most other fields of mathematics as well as important applications in physics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2007Количество страниц: 500Добавлена в каталог: 22.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Nonmeasurable linear function 262 Nonmeasurable norm 249 Nonmeasurable set 31 Normed space 249 Normed space, uniformly convex 284 Nowak M.T. 415 Number, ordinal 63 Ochan Yu.S. 415 437 Oden J.T. 414 Okikiolu G.O. 414 430 436 OlevskiT A.M. 261 Olmsted J.M.H. 414 Open set 2 Operation, set-theoretic 1 Operation, Souslin. 36 Ordered set 62 Ordinal 63 Ordinal, number 63 Orlicz space 320 Orlicz W. 307 320 Ort ho normal basis 258 Os C.H. van 411 Oscillation bounded mean 373 Osserman R. 379 Outer measure 16 41 Outer measure, Caratheodory 41 Outer measure, continuity from below 23 Outer measure, regular 44 Oxtoby J.C. 81 93 235 414 Pages G. 413 Paley R. 430 Pallara D. 379 Pallu de la Barriere R. 414 Panchapagesan T.V. 414 Panferov V.S. 415 Pannikov B.V. 435 Pap E. 415 423 433 Papageorgiou N.S. 413 Parseval equality 202 259 Parseval M.A. 202 259 Parthasarathy K.R. vi 414 Partially ordered set 62 Partition tagged 354 Pauc Ch.Y. 411 413 438 Paul S. 416 Pdlya G. 243 429 Peano G. 2 31 416 417 Peano — Jordan measure 2 31 Pecaric J.E. 429 Pedersen G.K. 414 Pedrick G. 413 Pelc A. 81 Pelczynski A. 174 Perimeter 378 Perron O. 437 Pesin I.N. 416 417 423 437 Pesin Y.B. 421 Pettis J. 422 434 Petty C.M. 215 Pfanzagl J. 419 Pfeffer W.F. 369 414 437 Phillips E.R. 414 416 Phillips lemma 303 Phillips R.S. 303 Picone M. 414 Pier J.-P. 416 417 423 Pierlo W. 419 Pierpont J. 410 Pilipenko A.Yu. 382 Pinsker M.S. 155 Pinsker — Kullback — Csiszar inequality 155 Pisier G. 431 Pitman J. 435 Pitt. H.R. 414 Plachky D. 414 Plancherel M. 237 430 Plancherel theorem. 237 Plessner A. 411 Podkorytov A.N. 415 Poincare H. 84 378 Poineare, formula 84 Poineare, inequality 378 Point, density 366 Point, Lebesgue 351 366 Polischuk E.M. 416 Pollard D. 414 Polynomials, Chebyshev — Hermite 260 Polynomials, Laguerre 304 Polynomials, Legendre 259 Ponomarev S.P. 382 Poroshkin A.G. 414 420 Portenier C. 415 Positive definite function 198 220 Possel R. de 438 Pothoven K. 414 Poulsen E.T. 246 Pratt J.W. 428 Preiss D. 404 437 Priestley H.A. 414 Probability, measure 10 Probability, space 10 Product of measures 181 Product of measures, infinite 188 Product, 180 Product, measure 181 Prohorov (Prokhorov, Prochorow) Yu.V. viii 417 Property, (N) 194 388 438 Property, Banach — Saks 285 Property, doubling 375 Ptak P. 244 Ptak V. 90 Pugachev O.V. 102 Pugachev V.S. 414 Pugh C.C. 414 Purely additive set function 219 Rademacher H. 85 Rado T. 102 437 Radon J. v vi viii 178 227 409 417 418 425 429 431 434 437 Radon transform 227 Radon — Nikodym density 178 Radon — Nikodym theorem 177 178 180 256 429 Ramachandran B. 430 Rana I.K. 414 Randolph J.F. 414 Rao B.V. 211 422 Rao K.P.S. Bhaskara 99 422 423 Rao M. Bhaskara. 99 423 Rao MM. 242 312 320 397 414 423 Ray W.O. 414 Real measurable cardinal 79 Real-valued function 9 Rectangle measurable 180 Reflexive Banach space. 281 Regular outer measure 44 Reichelderfer P.V. 102 Reinhold-Larsson K. 435 Reisner S. 246 Renyi A. 104 Reshetnyak Yu.G. 228 379 382 Restriction of a 56 Restriction of a measure 23 57 Revuz D. 414 Rey Pastor J. 414 RiceN.M. 431 Richard U. 414 Richter H. 414 Ricker W.J. 423 Rickert N.W. 244 Ricsz M. 295 434 Ridder J. 419 Riecan B. 423 Riemann B. v 138 309 416 Riemann integral 138 Riemann integral, improper 138 Riemann — Lebesgue theorem 274 Riesz F. v viii 112 163 256 259 262 386 409 412 417 424 425 426 430 431 434 Riesz theorem 112 256 262 Riesz — Fischer theorem 259 Ring of sets 8 Ring, generated by a semiring 8 Riviere T. 382 Rogers C.A. 90 215 422 430 Rogosinski W.W. 261 414 Rohlin (Rokhlin) V.A. viii 409 417 Romanovski P. 437 Romero J.L. 310 Rooij A.C.M. van 406 414 Rosenblatt J. 422 Rosenthal A. 410 415 418 419 421 Rosenthal H.P. 303 Rosenthal J.S. 414 Rosenthal lemma. 303 Ross K.A. 435 Rotar V.I. 414 Roussas C.G. 414 Rovden H.L. vi 414 Roy K.C. 414 Rubel L.A. 401 Rubio B. 413 Rubio de Francia J.L. 375 Ruch J-J. 435 Ruckle W.H. 414 Rudin W. 138 314 414 435 Rutickit Ja.B. 320 400 435 Ruziewicz S. 390 Ryll-Nardzewski C. 102 421 Saadoune M. 299 Saakyan A.A. 261 306 Sadovnichii V.A. 172 414 Saks S. 274 276 323 332 370 372 392 411 418 432 433 437 Saksman E. 376 Salem R. 142 435 Salinier A. 415 Samuelides M. 414 SansoneG. 411 414 426 Sarason D. 174 Sard A. 239 Sard, inequality 196 Saturated measure 97 Savage L. 7 279 Saxe K. 414 Saxena S.Ch. 414 Schaefer H.H. 281 Schafke P.W. 414 Schauder basis 296 Schauder J.P. 296 437 Schechtman G. 239 Scheffe H. 134 428 Scheffe theorem 134 428 Scheffer C.L. 431 Scheme, Souslin 36 Scheme, Souslin, monotone 36 Scheme, Souslin, regular 36 Schikhof W.H. 406 414 Schilling R. 414 Schlesinger L. 411 Schlumprecht T. 215 239 Schmets J. 413 Schmetterer L. 412 Schmitz N. 414 Schmuckenschlager M. 246 Schneider R. 431 Schonflies A. 410 Schwartz J.T. 240 282 283 321 413 415 421 423 424 434 435 Schwartz L. 376 414 Schwarz G. 141 428 Second mean value theorem 150 Section of a set 183 Segal I.E. 312 327 414 Semi-algebra of sets 8 Semi-ring of sets 8 Semiadditivity. 9 Seminnite measure 97 312 Seminorm 249 Semmes S. 437 Separable measure 54 91 306 Separable metric space 252 Sequence, convergent in 128 Sequence, convergent in measure 111 Sequence, convergent in the mean 128 Sequence, fundamental in 116 128 Sequence, fundamental in measure 111 Sequence, fundamental in the mean 116 128 Sequence, weakly convergent 281 Serov V.S. 415 Set function, additive 302 Set function, countably additive 9 Set function, countably-subadditive 11 Set function, monotone 17 41 70 71 75 Set function, subadditive 9 Set of full measure 110 Set, 36 Set, 36 Set, 17 21 Set, analytic 36 Set, Bernstein 63 Set, Besicovitch 66 Set, Borel 6 Set, bounded perimeter 378 Set, Caccioppolli 378 Set, Cantor 30 Set, closed 2 Set, cylindrical 188 Set, Erdos 422 Set, Lebesgue 352 Set, Lebesgue measurable 3 17 Set, locally measurable 97 Set, measurable 21 Set, measurable, Caratheodory 41 Set, measurable, Jordan 2 Set, measurable, Lebesgue 3 17 Set, measurable, with respect to 17 Set, Nikodym 67 Set, nonmeasurable 31 Set, open 2 Set, ordered 62 Set, partially ordered 62 277 Set, Sierpiriski 91 Set, Souslin 36 39 420 Set, well-ordered 62 Set-theoretic, operation 1 Set-theoretic, problem 77 Sets, metrically separated 104 Severini C. 426 Shabunin M.I. 415 Shah S.M. 414 Shakarchi R. 414 Sheftel Z.G. 413 Shilov G.E. 397 414 437 438 Shiryaev A.N. vi 414 Sierphiski W. 48 78 82 91 232 395 409 417 419 422 428 Sierpinski set 91 Sierpinski theorem 48 421 Signed measure 175 Sikorski R. 414 421 Simon L. 437 Simonelli I. 103 Simonnet M. 414 Simonovits M. 173 Simple function 106
Реклама
 |
|
О проекте
|
|
О проекте



 -algebra
-algebra 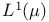
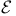 -analytic
-analytic  -measurable
-measurable