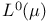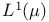Авторизация
Поиск по указателям
Bogachev V.I. — Measure Theory Vol.1
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure Theory Vol.1Автор: Bogachev V.I. Аннотация: Measure theory is a classical area of mathematics born more than two thousand years ago. Nowadays it continues intensive development and has fruitful connections with most other fields of mathematics as well as important applications in physics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2007Количество страниц: 500Добавлена в каталог: 22.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Cantelli F.P. 90 430 Cantor G. 30 193 416 417 Cantor, function 193 Cantor, set 30 Cantor, staircase 193 Capiriski M. 413 415 Caratheodary, measurability 41 Caratheodary, outer measure 41 Caratheodory C. v 41 100 409 410 417 418 419 420 421 Cardinal, inaccessible 79 Cardinal, measurable 79 Cardinal, nonmeasurable 79 Cardinal, real measurable 79 Cardinal, two-valued measurable 79 Carleman T. 247 Carlen E. 325 Carleson L. 260 Carleson theorem 260 Carlson T. 61 Carothers N.L. 413 436 Carter M. 425 Cauchy O. 141 428 Cauchy — Bunyakowsky inequality 141 255 Chacon R.V. 434 Chae S.B. 413 415 Chandrasekharan K. 413 Change of variables 194 343 Characteristic function of a measure 197 Characteristic function of a set 105 Characteristic functional 197 Chavel I. 379 Chebyshev inequality 122 405 Chebyshev P.L. 122 260 428 430 Chebyshev — Hermite polynomials 260 Chehlov V.I. 415 CheLidze V.C. 437 Cheney W. 413 Chentsov A.G. 423 Chong K.M. 431 Choquet G. 413 417 Chow Y.S. 413 Cichon J. 421 Ciesielski K. 81 87 Cifuentes P. 415 Cignoli R. 413 Clarkson inequality 325 Clarkson J.A. 325 Class, 33 Class, approximating 13 14 Class, approximating, compact 13 14 Class, Baire 148 Class, compact 13 50 189 Class, Lorentz 320 Class, monocompact 52 Class, monotone 33 48 Closed set 2 Cohn D.L. 413 Coifman R.R. 375 Compact class 13 50 189 Compactness in 321 Compactness in 295 317 Compactness, weak in 285 Compactness, weak in 282 Complete 22 Complete measure 22 Complete metric space 249 Complete normed space 249 Complete structure 277 Completion of a 22 Completion of a measure. 22 Complex-valued function 127 Constantinescu C. 413 Continuity from below of outer measure 23 Continuity of a measure at zero 10 Continuity, approximate 369 Continuum Hypothesis 78 conv A 40 Convergence in 128 Convergence in 298 Convergence in measure 111 306 Convergence in the mean 128 Convergence of measures setwise 274 291 Convergence, almost everywhere 110 Convergence, almost uniform 111 Convergence, almost weak in 289 Convergence, weak 281 Convergence, weak in 282 Convex, function 153 Convex, hull of a set 40 Convex, measure 226 378 Convolution of a function and a measure 208 Convolution of integrable functions 205 Convolution of measures 207 Cotlar M. 413 Countable additivity 9 24 Countable additivity, uniform 274 Countable subadditivity 11 Countably generated 91 Courrege P. 413 Cover 345 Cram MM. 430 Cramer H. 412 Craven B.D. 413 Criterion of compactness in 295 Criterion, de la Vallee Poussin 272 Criterion, integrability 136 Criterion, measurability 22 Criterion, uniform integrability 272 Criterion, weak compactness 285 Crittenden R.B. 91 Csiszar I. 155 Csornyei M. 234 Cuculescu I. 431 Cylinder 188 Cylindrical set 188 Dalen D. van 417 423 Dameter of a set 212 Danes S. 431 Daniell P.J. viii 417 419 423 429 Darboux G. 416 Darji U.B. 103 164 Darst R.B. 243 David G. 437 Davies R.O. 156 234 235 405 de Barm G. see “Barra G. de” de Guzman M. see “Guzman M. de” de la Vallee Poussin Ch.J. see “la Vallec Poussin Ch.J. de” de Mello E.A. see “Mello E.A. de” de Possel R. see “Possel R. de” De Wilde M. 413 Decomposable measure 96 235 313 Decomposition of set functions 218 Decomposition, Hahn 176 Decomposition, Jordan 176 220 Decomposition, Jordan Hahn 176 Decomposition, Lebesgue 180 Decomposition, Lebesgue, of a monotone function 344 Decomposition, Whitney 82 Degree of a mapping 240 Deheuvels P. 413 Delode C. 415 Demidov S.S. 416 Demkowicz L.F. 414 Denjoy A. 370 404 409 417 437 438 Denjoy — Young — Saks theorem 370 Denkowski Z. 413 Denneberg D. 423 Density of a measure 178 Density of a set 366 Density, point 366 Density, Radon — Nikodym 178 Density, topology 370 398 DePree J. 413 437 Derivate 331 Derivative 329 Derivative of a measure with respect to a measure 367 Derivative, approximate 373 Derivative, generalized 377 Derivative, left 331 Derivative, lower 332 Derivative, right 331 Derivative, Sobolev 377 Derivative, upper 332 Descombes R. 413 Determinacy, axiom 80 Dharmadhikari S. 431 DiBenedetto E. 413 Diestel J. 282 285 319 423 433 Dieudonne J. viii 413 Dieudonne theorem viii Differentiability, approximate 373 Differentiable function 329 Differentiation of measures 367 Dinculeanu N. 423 Dini condition 200 Dini U. 200 416 Dirac measure 11 Dirac P. 11 dist(a, B) 47 Distance to a set 47 Distribution function of a measure 32 Dixmiei J. 413 Dolzenko E.P. 403 Dominated convergence 130 Doob J.L. ix Dorogovtsev A.Ya. 413 415 Doubling property 375 Douglas R.G. 325 Drewnowski L. 319 423 433 Drinfeld V.G. 422 Dshalalow J.H. 413 Dual space 256 262 281 283 311 313 Dual to 266 313 431 Dual to 266 311 431 Dubins L.E. 435 Dubrovskii V.M. 324 433 Ducel Y. 415 Dudley R.M. 62 228 413 415 Dugac P. 416 432 Dunford N. 240 282 283 321 413 415 421 423 424 431 434 435 Durrett R. 413 Dynkin E.B. 420 Dzhvarsheishvili A.G. 437 D’yachenko M.I. 413 415 E* 262 281 283 E** 281 Earner M. 413 Eaton M.L. 431 Eberlein W.F. 282 434 Eberlein — Smulian theorem 282 Edgar G.A. 413 435 437 438 Edwards R.E. 261 423 Eggleston H.G. 235 Egoroff D.-Th. v 110 417 426 437 Egoroff theorem 110 426 Eisen M. 413 Elstrodt J. 413 415 Ene V. 436 Envelope, closed convex 282 Envelope, measurable 44 56 Equality of Parseval 259 Equimeasurable functions 243 Equivalence of functions 139 Equivalence of measures 178 Equivalent, functions 120 139 Equivalent, measures 178 Erdos P. 90 235 243 Erdos set 422 Escher J. 413 Essential value of a function 166 Essentially bounded function 140 essinf 167 esssup 167 250 Euclidean space 254 Evans C. 379 437 Evans M.J. 103 164 Example, Besicovitch 66 Example, Fichtenholz 233 Example, Kolmogorov 261 Example, Nikodym 210 Example, Vitali 31 Extension of a measure 18 22 58 Extension of a measure, Lebesgue 22 Extension of Lebesgue measure 81 Faber V. 240 Faden A.M. 423 Falconer K.J. 67 210 234 243 421 437 Farrell R.H. 308 Fatou P. 130 131 428 Fatou, lemma 131 Fatou, theorem 131 Federer H. 79 243 312 373 381 413 430 437 FeHermann C. 375 Fejer L. 261 Fejer sum 261 Fejzic H. 87 Feller W. 437 Fernandez P.J. 413 Fichera G. 413 Fichtenholz G. viii 134 234 276 344 391 392 396 411 428 432 433 435 Fichtenholz, example 233 Fichtenholz, theorem viii 271 433 Filter W. 413 422 Finitely additive, set function 9 303 Fink A.M. 429 First mean value theorem 150 Fischer E. 259 404 431 Fleming W. 414 Flohr F. 413 Floret K. 413 Folland G.B. 413 Fomin S.V. vi 62 65 67 412 424 Fominykh M.Yu. 435 Fonda A. 413 For an J. 413 Formula, area 380 Formula, change of variables 343 Formula, coarea 380 Formula, integration by parts 343 Formula, inversion 200 Formula, Newton — Leibniz 342 Formula, Poincare 84 Forster O. 414 Fourier J. 197 Fourier, coefficient 259 Fourier, transform 197 Franken P. 413 Frechet M. v 53 409 410 417 418 421 425 426 429 431 434 Frechet — Nikodym metric 53 418 Free tagged interval 353 Free tagged partition 354 Freilich G. 84 Freiling C. 87 Fremlm D.H. 53 74 78 80 98 100 235 237 312 325 413 421 434 Friedman H. 209 Fristedt B. 413 Frumkin P.B. 160 Fubini G. vi 183 185 336 409 429 Fubini theorem 183 185 209 336 409 429 Fukuda R. 169
Реклама
 |
|
О проекте
|
|
О проекте



 -additive
-additive