|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Silverman J. — The arithmetic of dynamical systems |
|
|
 |
| Предметный указатель |
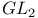 10 10
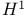 202 236 202 236
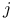 -invariant 221 337 -invariant 221 337
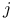 -invariant, in terms of cross-ratio 348 -invariant, in terms of cross-ratio 348
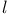 -adic representation 344 -adic representation 344
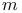 -torsion subgroup of elliptic curve 343 -torsion subgroup of elliptic curve 343
 -multiplier spectrum 182 -multiplier spectrum 182
 -multiplier spectrum, formal 182 -multiplier spectrum, formal 182
 -multiplier spectrum, of -multiplier spectrum, of 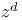 182 182
 -period polynomial 149 181 -period polynomial 149 181
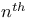 -dynatomic polynomial 149 181 -dynatomic polynomial 149 181
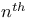 -dynatomic polynomial, homogeneous of degree -dynatomic polynomial, homogeneous of degree 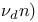 181 181
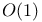 93 93
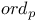 82 82
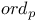 , of a polynomial 218 , of a polynomial 218
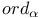 12 12
 -adic absolute value 44 -adic absolute value 44
 -adic Cauchy residue formula 314 -adic Cauchy residue formula 314
 -adic hyperbolic map 279 285 317 -adic hyperbolic map 279 285 317
 -adic inverse function theorem 312 -adic inverse function theorem 312
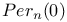 18 18
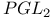 10 10
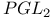 , , 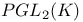 equivalence 195 233 equivalence 195 233
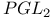 , action of Galois 203 , action of Galois 203
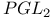 , automorphism group is subgroup 234 , automorphism group is subgroup 234
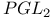 , cocycle gives twist of , cocycle gives twist of 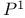 211 215 211 215
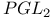 , conjugation is algebraic group action 173 , conjugation is algebraic group action 173
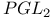 , equivalence 195 , equivalence 195
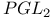 , extension of cocycle to , extension of cocycle to 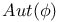 203 203
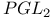 , finite subgroups 197 , finite subgroups 197
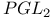 , invariant functions on , invariant functions on  175 175
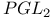 , is , is 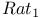 170 170
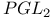 , is group variety 170 , is group variety 170
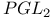 , map from , map from 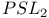 175 231 175 231
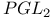 , minimal resultant is invariant 221 , minimal resultant is invariant 221
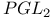 , quotient of , quotient of  by 174 by 174
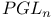 226 226
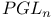 , map from , map from 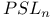 231 231
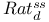 178 179 178 179
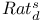 178 179 178 179
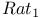 is is 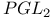 170 170
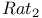 170 170
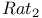 , normal forms lemma 190 233 , normal forms lemma 190 233
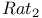 , subvariety with , subvariety with 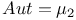 235 235
 169 169
 , , 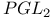 -invariant functions on 175 -invariant functions on 175
 , affine coordinate ring 169 174 , affine coordinate ring 169 174
 , coordinate ring contains , coordinate ring contains 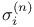 and and 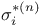 183 183
 , generic map not very highly ramified 231 , generic map not very highly ramified 231
 , geometry of boundary 170 , geometry of boundary 170
 , in , in 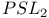 -stable locus 176 -stable locus 176
 , is a rational variety 232 , is a rational variety 232
 , is subset of , is subset of 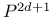 169 169
 , map induced by Schwarzian derivative 232 , map induced by Schwarzian derivative 232
 , map to , map to  174 174
 , multiplier 1 is Zariski closed subset 230 , multiplier 1 is Zariski closed subset 230
 , quotient by , quotient by 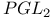 174 174
 , quotient by , quotient by 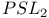 is a variety 175 is a variety 175
 , semistable rational maps 178 , semistable rational maps 178
 , stable rational maps 178 , stable rational maps 178
 , subvariety with nontrivial automorphisms 199 , subvariety with nontrivial automorphisms 199
 , universal map over 171 , universal map over 171
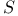 -unit in finite extension 132 -unit in finite extension 132
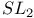 175 175
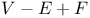 formula 13 37 formula 13 37
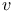 -adic chordal metric 45 144 -adic chordal metric 45 144
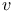 -adic chordal metric, effect of linear fractional transformation 76 -adic chordal metric, effect of linear fractional transformation 76
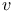 -adic chordal metric, invariant maps for 46 -adic chordal metric, invariant maps for 46
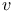 -adic chordal metric, is a metric 45 -adic chordal metric, is a metric 45
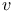 -adic chordal metric, periodic points 69 -adic chordal metric, periodic points 69
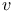 -adic chordal metric, relation to reduction 49 -adic chordal metric, relation to reduction 49
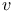 -adic chordal metric, resultant measures expansion 56 -adic chordal metric, resultant measures expansion 56
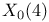 , , 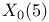 , , 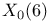 230 230
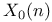 (dynatomic curve) 161 (dynatomic curve) 161
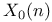 (dynatomic curve), is irreducible 164 (dynatomic curve), is irreducible 164
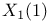 , , 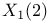 , , 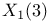 are rational 157 are rational 157
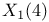 , , 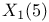 , , 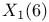 230 230
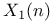 (dynatomic curve) 157 (dynatomic curve) 157
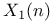 (dynatomic curve), action of (dynatomic curve), action of  on 161 on 161
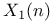 (dynatomic curve), genus 164 (dynatomic curve), genus 164
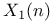 (dynatomic curve), is irreducible 164 (dynatomic curve), is irreducible 164
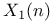 (dynatomic curve), is wreath product cover of (dynatomic curve), is wreath product cover of 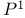 164 164
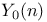 (dynatomic curve) 161 (dynatomic curve) 161
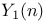 (dynatomic curve) 157 (dynatomic curve) 157
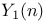 (dynatomic curve), action of (dynatomic curve), action of  on 161 on 161
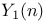 (dynatomic curve), is nonsingular 164 (dynatomic curve), is nonsingular 164
 20 20
 , acts on , acts on 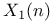 161 161
 , algebraic family 159 , algebraic family 159
 , algebraic family of 230 , algebraic family of 230
 , algebraic family, induces map to dynatomic curve 159 , algebraic family, induces map to dynatomic curve 159
 , bifurcation point 165 , bifurcation point 165
 , bifurcation polynomial 165 , bifurcation polynomial 165
 , condition for unequal formal and primitive periods 165 , condition for unequal formal and primitive periods 165
 , dynatomic curve 157 161 , dynatomic curve 157 161
 , dynatomic curve, , dynatomic curve, 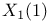 , , 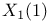 , , 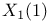 are rational 157 are rational 157
 , dynatomic curve, genus of 164 , dynatomic curve, genus of 164
 , dynatomic curve, is irreducible 164 , dynatomic curve, is irreducible 164
 , dynatomic curve, is modular curve 158 , dynatomic curve, is modular curve 158
 , dynatomic curve, is nonsingular 164 , dynatomic curve, is nonsingular 164
 , dynatomic curve, is wreath product cover of , dynatomic curve, is wreath product cover of 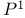 164 164
 , dynatomic polynomial 156 , dynatomic polynomial 156
 , Mandelbrot set 26 165 , Mandelbrot set 26 165
 , Mandelbrot set, in disk of radius 2 166 , Mandelbrot set, in disk of radius 2 166
 , map , map 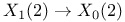 162 162
 , map , map 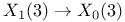 230 230
 , Misiurewicz point 166 , Misiurewicz point 166
 , no neutral cycles 166 , no neutral cycles 166
 , period polynomial 156 , period polynomial 156
 , points on dynatomic curve solve moduli problem 159 , points on dynatomic curve solve moduli problem 159
 , quadratic polynomial conjugate to 156 , quadratic polynomial conjugate to 156
 , repelling critical orbit 166 , repelling critical orbit 166
 , subhyperbolic 166 , subhyperbolic 166
 , with preperiodic critical point 166 , with preperiodic critical point 166
 tale map 353 tale map 353
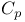 239 239
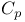 , bounded seminorm on on , bounded seminorm on on ![$\mathbb{C}_{p}[z]$](/math_tex/438e8f6f1b977bfdcd9bc501d9bcdbb582.gif) 296 296
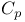 , Cauchy sequence 296 , Cauchy sequence 296
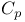 , compact Julia set example 275 , compact Julia set example 275
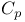 , is algebraically closed 239 242 , is algebraically closed 239 242
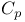 , is complete 242 , is complete 242
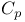 , is contained in Berkovich affine line 302 , is contained in Berkovich affine line 302
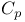 , is totally disconnected 239 276 294 , is totally disconnected 239 276 294
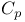 , not locally compact 239 294 , not locally compact 239 294
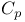 , projective space is bounded 243 , projective space is bounded 243
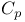 , projective space not compact 243 , projective space not compact 243
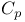 , unit disk contained in Berkovich disk 295 301 323 , unit disk contained in Berkovich disk 295 301 323
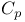 , valuation 249 , valuation 249
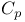 , value group is , value group is  294 294
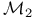 188 188
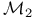 , completion equals , completion equals 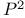 194 194
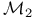 , explicit formula for , explicit formula for 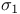 , , 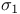 189 189
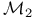 , is a rational variety 232 , is a rational variety 232
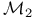 , is a scheme over , is a scheme over  189 189
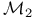 , isomorphic to , isomorphic to 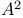 188 188
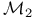 , locus of polynomial maps 232 , locus of polynomial maps 232
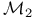 , point with , point with 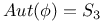 234 234
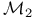 , subvariety with , subvariety with 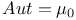 235 235
 174 174
 , , 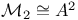 189 189
 , , 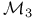 , embedded by , embedded by 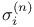 232 232
 , affine coordinate ring 176 , affine coordinate ring 176
 , coordinate ring contains , coordinate ring contains 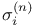 and and 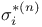 183 183
 , field of moduli 207 , field of moduli 207
 , generic map not very highly ramified 231 , generic map not very highly ramified 231
 , has dimension , has dimension 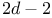 176 176
 , height 221 , height 221
 , is a rational variety? 232 , is a rational variety? 232
 , is a scheme over , is a scheme over  179 186 179 186
 , is a unirational variety 232 , is a unirational variety 232
|  , is a variety 175 , is a variety 175
 , is affine 176 , is affine 176
 , is complex orbifold 176 , is complex orbifold 176
 , is connected 176 , is connected 176
 , is integral 176 , is integral 176
 , is nonsingular? 193 , is nonsingular? 193
 , map from , map from  174 175 174 175
 , multiplier 1 is Zariski closed subset 230 , multiplier 1 is Zariski closed subset 230
 , not embedded by , not embedded by 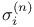 186 187 356 367 186 187 356 367
 , rational points 177 , rational points 177
 , semistable completion 178 , semistable completion 178
 , stable completion 178 , stable completion 178
 , subvariety with nontrivial automorphisms 199 234 , subvariety with nontrivial automorphisms 199 234
 , twists have same image 198 , twists have same image 198
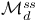 178 178
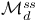 , is a scheme over , is a scheme over  179 179
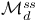 , is categorical quotient 179 , is categorical quotient 179
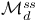 , is projective 178 , is projective 178
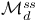 , isomorphic to , isomorphic to 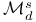 iff iff 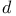 is even 178 is even 178
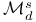 178 178
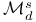 , has natural quotient property 179 , has natural quotient property 179
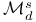 , is a scheme over , is a scheme over  179 179
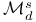 , is geometric quotient 179 , is geometric quotient 179
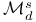 , is quasiprojective 178 , is quasiprojective 178
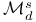 , isomorphic to , isomorphic to 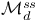 iff iff 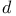 is even 178 is even 178
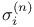 , isomorphism , isomorphism 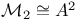 188 188
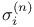 , of , of 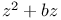 183 183
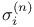 , of , of 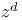 183 183
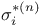 183 183
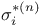 , for Latt , for Latt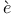 s map 186 s map 186
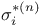 , in , in ![$\mathbb{Q}[\sigma_{1}, \sigma]$](/math_tex/40a760847e9d283ffcd274c92685bf6582.gif) for for 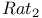 189 189
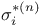 , is in , is in ![$\mathbb{Q}[\mathcal{M}_{d}]$](/math_tex/33c4d288691c849ada0c39c25115a6b882.gif) 183 232 183 232
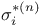 , of , of 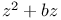 183 183
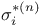 , of , of 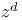 183 183
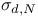 187 232 187 232
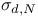 , degree unknown for , degree unknown for 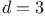 188 188
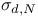 , embeds , embeds 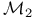 188 188
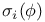 180 180
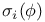 , explicit formula for , explicit formula for 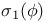 181 181
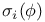 , is in , is in ![$\mathbb{Q}[\mathcal{M}_{d}]$](/math_tex/33c4d288691c849ada0c39c25115a6b882.gif) 180 180
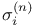 183 183
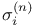 , explicit formula for , explicit formula for 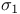 , , 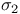 189 189
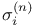 , for Latt , for Latt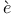 s map 186 s map 186
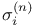 , in , in ![$\mathbb{Q}[\sigma_{1}, \sigma_{2}]$](/math_tex/cb6fd371ba2ec605775708abe672f17b82.gif) for for 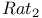 189 189
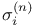 , integral over , integral over ![$\mathbb{Q}[Rat_{d}]$](/math_tex/9519453350660f541b01483e0b919abb82.gif) 185 185
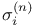 , is in , is in ![$\mathbb{Q}[\mathcal{M}_{d}]$](/math_tex/33c4d288691c849ada0c39c25115a6b882.gif) 183 183
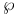 , Weierstrass function 34 345 , Weierstrass function 34 345
abc conjecture 372 373
Abelian group, preperiodic point equals torsion point 2 41 326
Abelian group, torsion subgroup 2
Abelian variety 409 442
Abelian variety, Bogomolov conjecture 129
Abelian variety, field of definition 217
Abelian variety, field of moduli 217
Abelian variety, Manin — Mumford conjecture 127
Abelian variety, N ron local height 104 ron local height 104
Abelian variety, Raynaud’s theorem 127
Absolute height 85
Absolute height, logarithmic 93
Absolute value 43
Absolute value,  -adic 44 82 -adic 44 82
Absolute value, Archimedean 82 83
Absolute value, completion of a field at an 83
Absolute value, effect of polynomial map on 288
Absolute value, equivalent 44
Absolute value, extension formula 83 84
Absolute value, local degree 83
Absolute value, nonarchimedean 44 82 83 242
Absolute value, of a point 90 288
Absolute value, of a polynomial 91 288
Absolute value, on  82 312 82 312
Absolute value, on function fields 44
Absolute value, product formula 83
Absolute value, standard set of (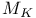 ) 83 ) 83
Abstract dynamical system 1
Abstract dynamical system, realizable sequence 6
Addition on an elliptic curve 31
Additive group 30
Additivity of height 408 421
Affine automorphism 390 427
Affine automorphism, algebraically reversible 429
Affine automorphism, algebraically stable 396 433
Affine automorphism, canonical height 431
Affine automorphism, composition of elementary maps and H non maps 402 non maps 402
Affine automorphism, composition of involutions 429
Affine automorphism, degree 394
Affine automorphism, degree of inverse 394 395
Affine automorphism, disjoint indeterminacy locus 394
Affine automorphism, dynamical degree 433
Affine automorphism, fixed point 427
Affine automorphism, H non map 390 non map 390
Affine automorphism, height inequality 399 431
Affine automorphism, height of periodic points 402
Affine automorphism, indeterminacy locus 389 392
Affine automorphism, indeterminacy locus, dimension of 394
Affine automorphism, indeterminacy locus, disjoint 394
Affine automorphism, indeterminacy locus, of inverse 392
Affine automorphism, indeterminacy locus, of iterate 394
Affine automorphism, inverse may have different degree 390
Affine automorphism, iterate may have wrong degree 390
Affine automorphism, number of orbits over a finite field 430
Affine automorphism, number of orbits over a finite field periodic points of 394 400
Affine automorphism, regular 391 394 427
Affine automorphism, regular periodic points of 428
Affine automorphism, reversible H non map 430 non map 430
Affine coordinate ring, of  169 174 169 174
Affine coordinate ring, of 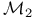 189 189
Affine coordinate ring, of  176 179 176 179
Affine coordinate ring, of  , as , as  -scheme 186 189 -scheme 186 189
Affine coordinate ring, of  , contains , contains 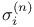 183 183
Affine coordinate ring, of  , contains , contains 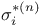 183 232 183 232
Affine line, Berkovich 301
Affine minimal model of a rational map 112 372 385
Affine minimal rational map 372
Affine morphism 375 388
Affine morphism, algebraically stable 396 433
Affine morphism, degree of composition 392
Affine morphism, dynamical degree 397 428
Affine morphism, finite quotient 376
Affine morphism, homogenization 389
Affine morphism, indeterminacy locus 389 392 427
Affine morphism, iterates 376
Affine morphism, jointly regular 397 429
Affine morphism, lift of 389
Affine morphism, uniquely determines endomorphism and translation 376
Affine plane, absolute value 288
Affine plane, lift of rational map 287
Affine plane, projection to projective line 287
Affine plane, with origin removed 287
Affine space, absolute value 90
Affine space, height 397
Affine space, projection to projective space 287
Algebraic closure 85
Algebraic dynamics 6
Algebraic entropy 397
Algebraic family 159 230
Algebraic family, field of definition 159
Algebraic family, induces map to dynatomic curve 159
Algebraic family, of 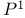 ’s 171 ’s 171
Algebraic family, of morphisms 171
Algebraic family, of quadratic maps 194
Algebraic geometry 402
Algebraic group 325
Algebraic group, commutative 375
Algebraic group, conjugation is action on 173
Algebraic group, finite quotient 376
Algebraic group, iterates of affine morphism 376
Algebraic group, simple 377
Algebraic group, universal cover 375
Algebraic point in Julia set 40
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



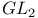
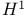
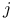 -invariant
-invariant 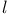 -adic representation
-adic representation 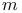 -torsion subgroup of elliptic curve
-torsion subgroup of elliptic curve  -multiplier spectrum
-multiplier spectrum 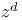
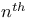 -dynatomic polynomial
-dynatomic polynomial 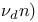
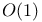
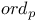
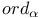
 -adic absolute value
-adic absolute value 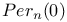
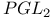
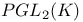 equivalence
equivalence 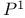
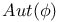

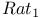
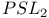
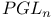
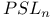
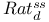
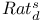
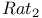
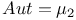
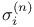 and
and 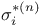
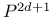

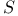 -unit in finite extension
-unit in finite extension 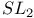
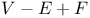 formula
formula 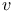 -adic chordal metric
-adic chordal metric 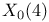 ,
, 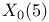 ,
, 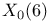
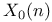 (dynatomic curve)
(dynatomic curve) 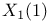 ,
, 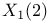 ,
, 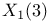 are rational
are rational 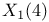 ,
, 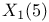 ,
, 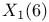
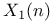 (dynatomic curve)
(dynatomic curve)  on
on 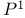
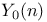 (dynatomic curve)
(dynatomic curve) 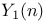 (dynatomic curve)
(dynatomic curve) 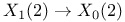
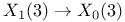
 tale map
tale map 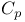
![$\mathbb{C}_{p}[z]$](/math_tex/438e8f6f1b977bfdcd9bc501d9bcdbb582.gif)

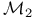
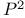
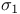 ,
, 
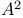
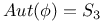
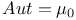
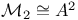
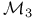 , embedded by
, embedded by 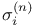 and
and 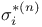
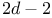
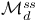
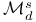 iff
iff 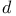 is even
is even 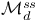 iff
iff 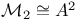
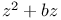
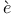 s map
s map ![$\mathbb{Q}[\sigma_{1}, \sigma]$](/math_tex/40a760847e9d283ffcd274c92685bf6582.gif) for
for ![$\mathbb{Q}[\mathcal{M}_{d}]$](/math_tex/33c4d288691c849ada0c39c25115a6b882.gif)
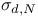
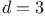
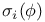
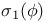
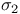
![$\mathbb{Q}[\sigma_{1}, \sigma_{2}]$](/math_tex/cb6fd371ba2ec605775708abe672f17b82.gif) for
for ![$\mathbb{Q}[Rat_{d}]$](/math_tex/9519453350660f541b01483e0b919abb82.gif)
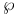 , Weierstrass function
, Weierstrass function 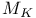 )
)