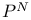|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Silverman J. — The arithmetic of dynamical systems |
|
|
 |
| Предметный указатель |
Induced rational map 389
Inertia group 344
Infinite dihedral group 419
Integer point, counting on Markoff variety 437
Integer point, cutoff for in orbits 375
Integer point, in orbit 3 108 109 112 143 145
Integer point, in orbit of 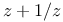 8 8
Integer point, on 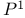 minus 3 points 106 minus 3 points 106
Integer point, on elliptic curve 372
Integer point, on Markoff variety 437
Integer point, orbits with many 110 111 143 375
Integer point, uniform bound in orbits 112 372 385
Integer point, value of rational function 143
Integrable map 429
Integrable map, level curve is elliptic curve 430
Integrable map, level set 431
Integrable map, McMillan family 443
Integrable map, QRT family 443
Intersection theory 434
Invariant differential 344 359 367
Invariant differential, is holomorphic 345
Invariant differential, is translation-invariant 345
Invariant differential, transformation for ![$[m]$](/math_tex/dd493f02a0fe43f96fae4e899577001182.gif) 345 345
Invariant measure 307
Invariant set 16
Invariant set, completely 17 266
Invariant set, contains Berkovich Julia set 311
Invariant set, Fatou and Julia sets are completely 23
Invariant set, finite 16 266
Inverse function theorem 115 144
Inverse function theorem, over 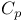 312 312
Inverse of point on elliptic curve 337
Inversion maps disk toj 321
Involution 410
Involution, action on divisor 418 419 438
Involution, as linear transform on Picard group 420
Involution, composition is reversible affine automorphism 429
Involution, degenerate point 415
Involution, eigenvalue of 421
Involution, formulas to compute 433
Involution, indeterminacy locus 413
Involution, induced by degree 2 map 411 437
Involution, is morphism on most K3 surfaces 417
Involution, noncommuting 410
Involution, not a morphism 436
Involution, on Markoff variety 436
Involution, quotient by 410
Involution, relation between noncommuting 419
Involution, surface in 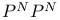 with two 436 with two 436
Involution, three noncommuting 437
Irrational number approximated by rational number 104
Irrationally neutral periodic point 19
Isogenous elliptic curves 339
Isogeny 339
Isogeny, degree 340
Isogeny, dual 340 352
Isogeny, is homomorphism 340
Isogeny, is unramified 340 353
Isolated point 402
Isolated point, Julia set contains no 25
Isolated point, of bounded height 402
Isolated point, periodic 402
Isolated point, preperiodic 8
Isospectral family 186 188 356 362
Iterate, coordinate functions of 149
Iteration commutes with conjugation 11
Itinerary 258
Itinerary, as map on sequence space 260
Itinerary, left shift 260
Jacobian variety 369
Jointly regular affine morphisms 397 429
Jointly regular affine morphisms, height inequality 397
Julia set 22 255
Julia set, algebraic points 40
Julia set, all of 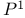 26 35 361 26 35 361
Julia set, backward orbit is dense 25
Julia set, Berkovich 306
Julia set, Berkovich, backward orbit dense in 311
Julia set, Berkovich, for bad reduction map 307 311
Julia set, Berkovich, for good reduction map 307 311
Julia set, Berkovich, has empty interior 311
Julia set, Berkovich, is connected or infinitely many components 311
Julia set, boundary is completely invariant 23
Julia set, boundary of Fatou set 25
Julia set, canonical height of points in 138
Julia set, chaotic behavior 22
Julia set, Chebyshev polynomial 30 41
Julia set, classical contained in Berkovich 306
Julia set, closure of repelling periodic points 41
Julia set, compact 275
Julia set, complement of Fatou set 22
Julia set, connected 26
Julia set, contained in closure of periodic points 273
Julia set, contains repelling periodic points 40 256
Julia set, disjoint from postcritical set closure 280
Julia set, effect of strictly preperiodic critical points 26
Julia set, equal to 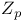 275 275
Julia set, equals closure of repelling periodic points 27 311
Julia set, filled 74 140
Julia set, Green function for filled 140
Julia set, has empty interior 267
Julia set, in two disks 257
Julia set, is closed 22
Julia set, is closure of backward orbit 267
Julia set, is completely invariant 23 74 266
Julia set, is empty for good reduction map 26 59 239
Julia set, is nonempty 25
Julia set, is perfect set 23 267 307 311
Julia set, is uncountable 267 307 311
Julia set, local canonical height of points in 141
Julia set, no critical points 285
Julia set, nonarchimedean 254
Julia set, nonempty interior 26
Julia set, of 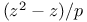 262 283 262 283
Julia set, of 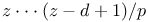 315 315
Julia set, of 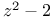 40 40
Julia set, of 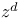 22 22
Julia set, of an iterate 24 255
Julia set, of Chebyshev polynomial 336
Julia set, of commuting maps 378
Julia set, of Latt s map 35 361 s map 35 361
Julia set, open set orbit omits at most one point 266
Julia set, orbit of open subset 27
Julia set, periodic points dense 23 315
Julia set, smallest closed completely invariant set 267
Julia set, strictly expanding map on 279 317
Julia set, support of canonical measure is 307
Julia set, topologically transitive map 263 315
Julia set, totally disconnected 23 26
Julia set, with no critical points 279
K3 surface 410
K3 surface, 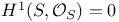 412 412
K3 surface, 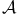 orbit 418 orbit 418
K3 surface, action of involution on divisors 418 438
K3 surface, arithmetic complexity of orbit 435
K3 surface, canonical height 421 423 435
K3 surface, canonical height, infinitely many points of bounded 435
K3 surface, canonical height, normalization conditions 422
K3 surface, canonical height, product 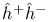 435 435
K3 surface, canonical height, transformation formulas 422
K3 surface, canonical height, zero iff finite orbit 423
K3 surface, degenerate point for involution 415
K3 surface, dimension of family of 412 438
K3 surface, divisors on 418
K3 surface, eigenvalue of involution on divisors 421 438
K3 surface, finitely many periodic points 435
K3 surface, finitely many points of bounded canonical height 423
K3 surface, Galois-invariant orbit 436
K3 surface, height functions on 420
K3 surface, height transformation rules 420
| K3 surface, height zeta function 436
K3 surface, homogeneous forms associated to 412
K3 surface, in 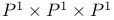 437 437
K3 surface, indeterminacy locus of involution 413
K3 surface, intersection theory 434
K3 surface, involution 411
K3 surface, involution, as linear transform on Picard group 420
K3 surface, involution, example 411
K3 surface, involution, formulas 433
K3 surface, involution, is morphism on most 417 438
K3 surface, Kodaira dimension 412
K3 surface, nonsingular 438
K3 surface, number of points of bounded height 425
K3 surface, orbit is Zariski dense 435
K3 surface, Picard group of general 418
K3 surface, projections to 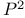 410 410
K3 surface, relation between noncommuting involutions 419
K3 surface, stabilizer of point on 425 434
K3 surface, with three involutions 437 438
Kawaguchi’s theorem 399
Kodaira dimension 412
Kronecker’s theorem 88 100
Krylov — Bogolubov theorem 127
Kummer sequence 205
L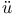 roth’s theorem 158 roth’s theorem 158
Lang’s height lower bound conjecture 101
Lang’s integer points conjecture 112
Latt s diagram 365 s diagram 365
Latt s map 32 97 186 187 351 s map 32 97 186 187 351
Latt s map, affine minimal 372 385 s map, affine minimal 372 385
Latt s map, commuting 378 s map, commuting 378
Latt s map, composition of 382 s map, composition of 382
Latt s map, critical point of s map, critical point of  384 384
Latt s map, critical values 353 s map, critical values 353
Latt s map, cutoff for integral points in orbit 375 s map, cutoff for integral points in orbit 375
Latt s map, defining equation 32 351 s map, defining equation 32 351
Latt s map, degree 34 s map, degree 34
Latt s map, fixed points 34 366 382 384 s map, fixed points 34 366 382 384
Latt s map, flexible 355 s map, flexible 355
Latt s map, for multiplication-by- s map, for multiplication-by-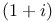 32 32
Latt s map, for multiplication-by-2 32 351 370 s map, for multiplication-by-2 32 351 370
Latt s map, for multiplication-by-2, on s map, for multiplication-by-2, on 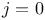 curve 351 381 curve 351 381
Latt s map, for multiplication-by-2, on s map, for multiplication-by-2, on 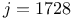 curve 351 curve 351
Latt s map, good reduction 362 383 s map, good reduction 362 383
Latt s map, higher-dimensional 377 s map, higher-dimensional 377
Latt s map, in characteristic s map, in characteristic 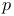 366 366
Latt s map, integral s map, integral 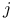 -invariant 370 -invariant 370
Latt s map, isospectral family 362 s map, isospectral family 362
Latt s map, iterate 382 s map, iterate 382
Latt s map, multiplier 34 186 358 366 382 384 s map, multiplier 34 186 358 366 382 384
Latt s map, multiplier, at s map, multiplier, at  383 383
Latt s map, multiplier, of fixed point 382 s map, multiplier, of fixed point 382
Latt s map, multiplier, spectrum 362 s map, multiplier, spectrum 362
Latt s map, multiplier, summation formula 382 s map, multiplier, summation formula 382
Latt s map, nonconjugate 354 s map, nonconjugate 354
Latt s map, nonconjugate, in characteristic 2 383 s map, nonconjugate, in characteristic 2 383
Latt s map, nonconjugate, to polynomial 381 s map, nonconjugate, to polynomial 381
Latt s map, padically s map, padically 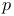 -adically 361 -adically 361
Latt s map, periodic points 186 358 366 382 384 s map, periodic points 186 358 366 382 384
Latt s map, periodic points, all attracting 362 s map, periodic points, all attracting 362
Latt s map, periodic points, all nonrepelling 362 s map, periodic points, all nonrepelling 362
Latt s map, periodic points, expanding 35 s map, periodic points, expanding 35
Latt s map, periodic points, in Julia set 35 361 s map, periodic points, in Julia set 35 361
Latt s map, postcritical set 353 s map, postcritical set 353
Latt s map, postcritically finite 353 s map, postcritically finite 353
Latt s map, preperiodic points 32 352 s map, preperiodic points 32 352
Latt s map, projection to s map, projection to 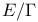 365 365
Latt s map, reduced diagram 365 s map, reduced diagram 365
Latt s map, rigid 364 s map, rigid 364
Latt s map, set of is monoid 382 s map, set of is monoid 382
Latt s map, torsion points map to preperiodic points 41 s map, torsion points map to preperiodic points 41
Latt s map, translation fixed by s map, translation fixed by 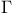 365 365
Latt s map, uniform bound for integral points in orbit 372 385 s map, uniform bound for integral points in orbit 372 385
Latt s map, uniform boundedness of periodic points 137 s map, uniform boundedness of periodic points 137
Lattice 33
Laurent series 245
Laurent series, coefficients uniquely determined by function 312
Laurent series, of Schwarzian derivative 232
Laurent series, product of 312
Least period see exact period
Lefschetz principle 20 365
Left shift map 259 314
Left shift map, as itinerary map 260
Left shift map, backward orbit dense 314
Left shift map, backward orbit equidistributed 315
Left shift map, continuous 259
Left shift map, is topologically transitive 259
Left shift map, Lipschitz 259
Left shift map, periodic points 259
Left shift map, periodic points, are dense 314
Left shift map, properties of 259
Left shift map, topologically transitive 314
Left shift map, uniformly expanding 259
Lehmer’s conjecture 100 138
Lehmer’s conjecture, dynamical 101 138
Level curve of integrable map 430
Level set of an integrable map 431
Lie group 6
Lift 287
Lift, from 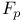 to to 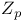 48 48
Lift, of affine morphism 389
Lift, of rational map 287 389
Line bundle, metrized 410
Line segment, from Gauss point to Type — IV point 322
Line segment, in Berkovich disk 298
Line segment, of Newton polygon 249
Linear conjugation 11 173
Linear conjugation, commutes with iteration 11
Linear equivalence 403
Linear equivalence, divisors give same height 408
Linear equivalence, pullback preserves 405
Linear fractional transformation 10
Linear fractional transformation, action of Galois 203
Linear fractional transformation, chordal sup norm 269
Linear fractional transformation, distance between images 269 316
Linear fractional transformation, effect on chordal metric 76
Linear fractional transformation, image of unit disk 317
Linear fractional transformation, Lipschitz constant 36
Linear fractional transformation, move three points 36
Linear fractional transformation, on 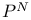 226 226
Linear fractional transformation, resultant of 76
Linear group, general 10
Linear group, projective special 175
Linear group, special 175
Lipschitz 11 24 36 56
Lipschitz, equi- 313
Lipschitz, holomorphic function 248 254 272
Lipschitz, shift map 259
Lipschitz, uniform family 39 254 264 265
Local canonical height 102 291
Local canonical height, associated to a divisor 320
Local canonical height, associated to an eigendivisor class 104
Local canonical height, computation of 103
Local canonical height, existence proof 291
Local canonical height, for a polynomial map 103 140 141
Local canonical height, good reduction case 103 141
Local canonical height, Green function and 291
Local canonical height, is harmonic 140
Local canonical height, Laplacian is invariant measure 104
Local canonical height, normalized 141
Local canonical height, of point in Fatou or Julia set 141
Local canonical height, properties of 102 291 320
Local canonical height, sum to global canonical height 103 293
Local canonical height, transformation law 320
Local degree 83
Local ring 67 79
Local ring, at a divisor 403
Local ring, normalized valuation 403
Locally compact 74 243 304
Locally compact, 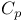 is not 239 268 294 295 is not 239 268 294 295
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 minus 3 points
minus 3 points ![$[m]$](/math_tex/dd493f02a0fe43f96fae4e899577001182.gif)
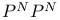 with two
with two 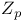
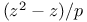
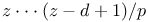
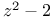
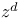
 s map
s map 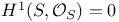
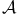 orbit
orbit 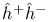
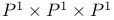
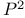
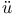 roth’s theorem
roth’s theorem 
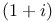
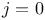 curve
curve 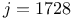 curve
curve 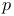
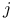 -invariant
-invariant 
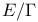
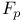 to
to