|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimaldi R.P. — Discrete and combinatorial mathematics. An introduction |
|
|
 |
| Предметный указатель |
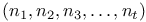 28 28
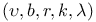 -design 865—867 872 874 -design 865—867 872 874
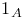 280 280
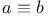 (mod n) 717 (mod n) 717
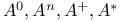 322 322
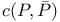 674 674
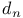 418—420 418—420
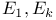 388 388
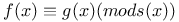 846 846
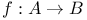 251 251
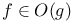 294 294
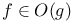 on S 513 on S 513
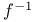 285 285
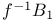 287 287
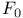 (contradiction) 58 86 (contradiction) 58 86
 ( (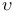 vertex) 540 vertex) 540
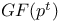 851 857 871 851 857 871
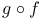 281 281
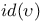 554 554
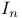 361 361
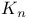 366 491 540 366 491 540
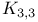 561 562 561 562
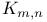 561 561
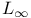 869 869
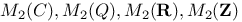 702 702
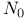 (aleph null) A-35 A-36 (aleph null) A-35 A-36
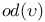 554 554
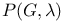 590 590
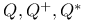 153 153
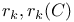 421 421
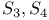 783 783
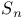 783 830 783 830
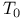 (tautology) 58 (tautology) 58
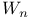 537 537
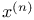 606 606
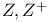 153 153
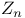 153 717 153 717
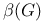 587 587
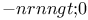 438 438
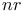 19 44 45 438 19 44 45 438
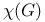 588—591 588—591
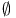 (the null set) 100 (the null set) 100
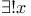 120 120
 100 100
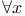 100 145 100 145
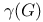 603 603
 (the empty string) 316 (the empty string) 316
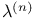 591 591
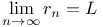 121 121
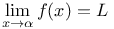 113 114 113 114
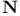 153 153
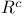 (converse of relation (converse of relation 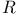 ) 284 ) 284
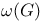 605 605
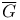 541 541
 (Euler’s phi function) 409—411 720 779 (Euler’s phi function) 409—411 720 779
 notation 235 notation 235
 notation 22 notation 22
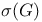 689 689
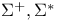 317 317
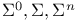 316 316
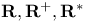 153 153
(0, l)-matrix 359 395
(i, j)-entry of a matrix A-13
(n, m) block code 796 (see also “Algebraic coding theory”)
1-equivalence 350
1-equivalent states 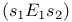 388 388
2-isomorphic graphs 576
2-methyl propane 610
a - z cut 673
a is congruent to b modulo n 717
Abel, Niels Henrik 730 777 830 872
Abelian group 173 777
abs 216
Absorption Laws, for a Boolean algebra 764
Absorption Laws, for Boolean functions 737
Absorption Laws, for Boolean variables 737
Absorption Laws, for logic 65
Absorption Laws, for set theory 160
Access function 253 259
Access permissions 17
Achilles 139
Ackermann, Wilhelm 260
Ackermann’s function 259 260
Addition of binary numbers 746
Addition of equivalence classes of integers (in 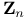 ) 718 ) 718
Addition of equivalence classes of polynomials 846
Addition of matrices A14
Addition of polynomials 836
Additive identity for matrices A 15
Additive identity for real numbers 120
Additive inverse of a matrix A 15
Additive inverse of a real number 120
Additive inverse of an integer 280
Address in a universal address system 616
Address in computer memory 5 720
Adjacency list 397
Adjacency list representation 395 397
Adjacency matrix for a graph 367 559
Adjacent from 363 530
Adjacent mark ordering algorithm 523
Adjacent to 363 530
Adjacent vertices 363 530
Affine plane 859—864 866—868
Aho, Alfred V. 395 396 523 600 601 651 652 670 694 695
Al-jabr 288
Al-Khowarizmi, Abu Ja’far Mohammed ibn Musa 238 239
Albert, A. Adrian 872 873
Aleph 310
Algebra of propositions 61 63 64
Algebra of switching circuits 772
Algebra of switching functions 735
Algebraic coding theory 23 173 777 793—811 831
Algebraic coding theory, (n, m) block code 796
Algebraic coding theory, binary symmetric channel 794
Algebraic coding theory, block code 796
Algebraic coding theory, code word 795
Algebraic coding theory, coding schemes 795—797
Algebraic coding theory, coset leader 808
Algebraic coding theory, d(x, y) 798
Algebraic coding theory, decoding 796 804
Algebraic coding theory, decoding algorithm 804
Algebraic coding theory, decoding by coset leaders 809
Algebraic coding theory, decoding table 807 808
Algebraic coding theory, decoding table with syndromes 809
Algebraic coding theory, distance 798
Algebraic coding theory, distance function 799
Algebraic coding theory, dual code 805
Algebraic coding theory, efficiency of a coding scheme 796
Algebraic coding theory, encoding 795 801 804
Algebraic coding theory, equivalent codes 811
Algebraic coding theory, error correction 800
Algebraic coding theory, error detection 800
Algebraic coding theory, error pattern 794
Algebraic coding theory, five-times repetition code 798
Algebraic coding theory, generator matrix 801 806 807
Algebraic coding theory, Gilbert bound 806
Algebraic coding theory, Golay, Marcel 793
Algebraic coding theory, group code 806
Algebraic coding theory, Hamming bound 806
Algebraic coding theory, Hamming code 811
Algebraic coding theory, Hamming matrix 811
Algebraic coding theory, Hamming metric 799
Algebraic coding theory, Hamming, Richard 793 794 798
Algebraic coding theory, independent events 794
Algebraic coding theory, majority rule 797 798
Algebraic coding theory, message 794 795
Algebraic coding theory, metric 799
Algebraic coding theory, metric space 799
Algebraic coding theory, nearest neighbor 803
Algebraic coding theory, nine-times repetition code 805
| Algebraic coding theory, noise 794
Algebraic coding theory, parity-check code 797
Algebraic coding theory, parity-check equations 802
Algebraic coding theory, parity-check matrix 804 806 807 811
Algebraic coding theory, probability 794—797
Algebraic coding theory, rate of a code 796 811
Algebraic coding theory, received word 795
Algebraic coding theory, S(x, k) 799
Algebraic coding theory, Shannon, Claude Elwood 793
Algebraic coding theory, sphere (S(x, k)) 799
Algebraic coding theory, syndrome 803
Algebraic coding theory, systematic form 811
Algebraic coding theory, triangle inequality 799
Algebraic coding theory, triple repetition code 797
Algebraic coding theory, weight of x 798
Algebraic coding theory, wt(x) 798
Algebraic structures 794
Algorism 238
Algorithm 44 45 227 238 239 293 294 297—305 511 512
Algorithms, adjacent mark ordering 467 468 523
Algorithms, binary search 517—519
Algorithms, breadth-first search 626
Algorithms, constructing a Huffman tree 642 643
Algorithms, counting nonisomorphic labeled trees 613 614
Algorithms, decoding 804
Algorithms, depth-first search 624
Algorithms, determining articulation points 647 651
Algorithms, Dijkstra’s shortest-path algorithm 660
Algorithms, divide-and-conquer algorithms 511—520 523 634
Algorithms, division algorithm for integers 215—218 225 226 231 253 276 278 293 717 788 789
Algorithms, division algorithm for polynomials 839—841 845—847
Algorithms, Euclidean algorithm for integers 226—229 293 468 469 522 719
Algorithms, Euclidean algorithm for polynomials 845
Algorithms, exponentiation 302
Algorithms, generating permutations 467 468
Algorithms, greatest common divisor 229
Algorithms, greatest common divisor (recursive) 469
Algorithms, Kruskal’s algorithm 666
Algorithms, labeling procedure 676 677
Algorithms, Merge Sort 637 638
Algorithms, merging two sorted lists 635
Algorithms, minimization process (finite state machine) 389
Algorithms, Prim’s algorithm 669
Algorithms, searching an unsorted array 300 301
Algorithms, topological sorting algorithm 375 376
Algorithms, universal address system 616
Alkane 610
Allowable choices 99
Alphabet 23 316
Alternative form of mathematical induction see “Mathematical induction” “Alternative
American Journal of Mathematics 428
An Investigation in the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probability 138
An Investigation of the Laws of Thought 176 735 772
Analysis of Algorithms 3 245 260 296—305 311 485 486 A-8
Analytic Theory of Probability 173
Analytical engine 239
Analytische Zahlentheorie 310
Ancestor 615
AND 52
AND gate 171 745
ANSI FORTRAN 145 384
Antichain 400
Antisymmetric property (of a relation) 352 353 367 373 394
Anton, Howard A 24
AP(F) 860
Apianus, Petrus 178
Appel, Kenneth 589 599—601
ARC 330 363
Argue by the converse 85 127
Argue by the inverse 85 128
Argument 51 58 77 80 124
Aristotle 137 138 233
Arithmetica 239
Arithmetica Integra 45
Arrangement 6—12 19—23 33 35 44 316 418 428 449 450
Arrangement (circular) 11 12
Arrangements with forbidden positions 424—426
Ars Conjectandi 44
Articulation point 577 645—647 651
Articulation point algorithm 647 651
Aschbacher, Michael 831
Assignment problem 683 695
Associated homogeneous relation 483 484 489 490
Associated undirected graph 364 533
Associative binary operation 268
Associative law of addition for integers 132
Associative law of addition for real numbers 111
Associative law of multiplication for matrices A-18
Associative laws for a Boolean algebra 764
Associative laws for a ring 701 702
Associative laws for Boolean functions 737
Associative laws for Boolean variables 737
Associative laws for logic 64 108
Associative laws for set theory 160
Associative property for composition of relations 358
Associative property for function composition 283
Associative property in a group 777 830
Atkins, Joel E. 651 652
Atom of a Boolean algebra 767 773
Augarten, Stan 239 241
Auluck, F. C 476 523
Automata theory 343
Auxiliary variables 474
Average-case complexity 300 301
Baase, Sara 311 651 652 668 670 694 695
Babbage, Charles 239
Bachmann, Paul Gustav Heinrich 310
Back edge (of a tree) 646
Backtrack(ing) 621 624
Balanced (rooted) tree 629
Balanced complete binary tree 634
Balanced incomplete block design 865 866 869
Ballot problem 50
Barnette, David 600 601
Barnier, William J. 343 344
Barwise, Jon 139 140
Base A-1 2 8 16 218—220
Base (for a number system) 218
Base (for a recursive definition) 202
Base-changing formula A-8
BASIC 6 55 60 253 618 726
Basic connectives 52—54 75 100 101
Basic connectives and (conjunction) 52
Basic connectives but 54
Basic connectives exclusive or 52
Basic connectives if and only if (biconditional) 53
Basic connectives if... then (implication) 52
Basic connectives inclusive or (disjunction) 52
Basic connectives nand 75
Basic connectives negation (not) 52
Basic connectives nor 75
Basic connectives not (negation) 52
Basic connectives or (disjunction) 52
Basic connectives quantifiers 100
BASIC program for complex number arithmetic 727
Basis step 185 186 188 189 196
Beckenbach, Edwin F. 832
Behzad, Mehdi 599 601
Bell numbers 524
Bell, Eric Temple 524
Bellman, R. 585 600 601
Bellmore, M. 585 600 601
Berge, Claude 599 695
Berger, Thomas R. 732 872 873
Bernays, Paul 139
Bernoulli trial 173
Bernoulli, Jakob 44
Bernoulli, Johann 308
Bertrand, Joseph Louis Frangois 50
Best case complexity 300 301
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



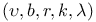 -design
-design 
 (mod n)
(mod n) 
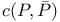
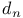
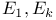
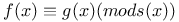
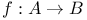
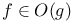
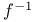
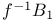
 (contradiction)
(contradiction)  (
( vertex)
vertex) 
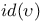
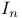
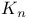
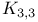
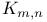
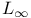
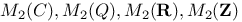
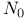 (aleph null)
(aleph null) 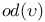
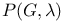
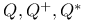
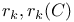
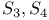
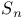
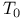 (tautology)
(tautology) 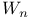
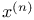
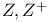
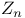
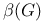
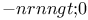
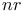
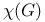
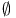 (the null set)
(the null set) 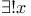

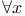
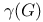
 (the empty string)
(the empty string) 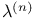
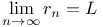
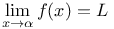
 (converse of relation
(converse of relation 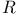 )
) 
 (Euler’s phi function)
(Euler’s phi function)  notation
notation  notation
notation 
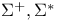
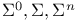
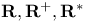
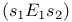
 )
)