|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph theory |
|
|
 |
| Предметный указатель |
 -system 271 -system 271
 -regular pair 176 191 -regular pair 176 191
 -regular partition 176 -regular partition 176
'Wagner's Conjecture' see graph minor theorem
,-chromatic 111 134
3-colour theorem see three colour theorem
4-colour theorem see four colour theorem
5-colour theorem see five colour theorem
Above 15
Abstract dual 105—106 108
Abstract graph 3 83 86 92 302
Acyclic 13—14 48 134
Adhesion 340 341
Adjacency matrix 28 32
Adjacent 3
Aharoni, R. 217 223 225 226 245 247 248
Ahuja, R.K. 161
Algebraic colouring theory 137
Algebraic flow theory 144—159 161
Algebraic graph theory 23—28 32
Algebraic planarity criteria 101—102
Algorithmic graph theory 161 349 355—356
Almost 302 312—313
Alon, N. 10 32 122 137—138 314
Alternating path 34 224
Alternating walk 64
Andreae, Th. 207 245 246
Antichain 51 53 241 316 388 389
Antihole 138
Apex vertices 340 353
Appel, K. 137
Arboricity 46—49 115 190 235 250
ARC 84 229 243 247 248 361 385
Arc-component 229 243
Arc-connected 229 243 248
Archdeacon, D. 355
Arnborg, S. 355
Articulation point see cutvertex
AT 2
Augmenting path for matching 34 51 224 241 371
Augmenting path for network flow 143 160
Automorphism 3 31 215 239 374
Average degree 5
Average degree and choice number 122
Average degree and chromatic number 117 122 169 172 190
Average degree and connectivity 12
Average degree and girth 8 9—10 301
Average degree and list colouring 122
Average degree and minimum degree 5—6
Average degree and number of edges 5
Average degree and Ramsey numbers 273
Average degree and regularity lemma 176 191
Average degree of bipartite planar graph 376
Average degree, bounded 273
Average degree, forcing minors 163 170—171 191 192—194
Average degree, forcing topological minors 70 169—
Back-and-forth technique 213—214 383
Bad sequence 316 354
Balanced 308
Bauer 291
Behzad, M. 138
Bellenbaum, P. 355
Below 15
Berge, C. 128
Berger, E. 217 247
BETWEEN 6 84
Biggs, N.L. 32
Binary tree 203 238
Bipartite graphs 17—18 31 107 111 127
Bipartite graphs in Ramsey theory 263—264 272
Bipartite graphs, edge colouring of 119 135 136
Bipartite graphs, flow number of cubic 150
Bipartite graphs, forced as subgraph 169 183
Bipartite graphs, list-chromatic index of 125—126 138
Bipartite graphs, matching in 34—39 222—224
Birkhoff, G.D. 137
Block 55 108 372
Block graph 56 78 372
Boehme, T. 81 193
Bollobas, B. 54 80 192 193 245 272 291 304 305 313 314 356
BOND 25 31 56 104—106 110 238
Bond space see cut space
Bond-cycle duality 104—106 152—154
Bondy, J.A. 291
Boundary of a face 89—90 107 363
Boundary of a wave 218
Boundary, circle 361
Bounded graph conjecture 238 239 244—245
Bounded subset of 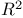 86 361 86 361
Bramble 322—324 351 353 355
Bramble number 324
Bramble, order of 322
Branch in tree-decomposition 325
Branch set 19
Branch vertex 20
Brandt, S. 192
Bridge 11 41 141 151 156—157
Bridge to bridge 281
Broersma 291
Brooks theorem 115 137
Brooks theorem, list colouring version 137
Brooks, R.L. 115 134
Bruhn, H. 110 247 248 278 291
Burr, S.A. 272
Cameron, P.J. 246
Capacity 142
capacity function 141
Cardinality 357
Catlin, P.A. 193
Cayley, A. 137 313
Central face in grid 342
Central vertex 9 342 369
Centre 17
Certificate 126 341 356 390
Chain 15 51 53 241 358 360
Chebyshev inequality 308 388
Cherlin, G. 246
Choice number 121
Choice number and average degree 122
Choice number of bipartite planar graphs 135
Choice number of planar graphs 122
Chord 8
Chordal 127—128 136 326 352 391
Chordal, supergraph 391
Chromatic index 112 119
Chromatic index and maximum degree 119—121
Chromatic index of bipartite graphs 119
Chromatic index vs. list-chromatic index 121 124
Chromatic number 111 134 155 201 244 353
Chromatic number and 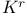 -subgraphs 116—117 126 226 -subgraphs 116—117 126 226
Chromatic number and average degree 117 122 169 172 190
Chromatic number and colouring number 115
Chromatic number and connectivity 116—117
Chromatic number and flow number 155
Chromatic number and girth 117 137 175 301
Chromatic number and maximum degree 115
Chromatic number and minimum degree 115 116
Chromatic number and number of edges 114
Chromatic number as a global phenomenon 117 126
Chromatic number in extremal graph theory 168
Chromatic number of almost all graphs 304
Chromatic number vs. choice number 121
Chromatic number, constructions 117—118 134 137
Chromatic number, forcing a triangle 135 271
Chromatic number, forcing minors 172—175 190 191 193—194
Chromatic number, forcing short cycles 117 301
Chromatic number, forcing subgraphs 116—117 238 271
Chromatic polynomial 134 162
Chudnovsky, M. 128 138
Chvatal, V. 256 278 279 291
| Circle in graph with ends 106 230 231 361
Circle in surface 348 361 362 365
Circle, boundary circle 361
Circle, one/two-sided 362
Circle, unit circle 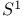 361 361
Circuit 23 231 242
Circulation 140—141 153 162
Circumference 8 351
Circumference and connectivity 79 276
Circumference and minimum degree 8
Class 1 vs. class 2 121
Classification of surfaces 361— 362
Clique number 126—133 263 326
Clique number of a random graph 296
Clique number, threshold function 312
Closed under addition 144 232
Closed under infinite sums 235
Closed under isomorphism 3 302 327
Closed up or down, in tree-order 15
Closed walk 10 22
Closed wrt. minors 135 160 245 327 341 342 349 352
Closed wrt. subgraphs 126 135
Closed wrt. supergraphs 126 305
Closure (of a set) 227
Cocycle see cut
Colour class 111
Colour-critical see critically k-chromatic
Colouring 111—138 173 201
Colouring algorithms 114 133
Colouring and flows 152—155
Colouring in Ramsey theory 253
Colouring number 114 134 135 245
Colouring plane graphs 112—113 152—155
Colouring, total 135 138
Comb 196 242
Comb, modified 240
Comb, star-comb lemma 204
Combinatorial isomorphism 93 94 107 108
Combinatorial set theory 250 272
Comfort, W.W. 250
Compactness 201 227 229 242
Compactness, proof technique 200 235—237 238 245
Comparability graph 127 136
Compatible separations 351
Complement and perfection 129 376
Complement of a bipartite graph 127 135
Complement of a graph 4
Complement of a property 327 341
Complete bipartite graph 17
Complete graph 3 150
Complete infinite graph 197 341
Complete matching see 1-factor
Complete minor 97 101 169—175 190 191 193—194 340—341 347—348
Complete multipartite graph 17 167
Complete part of path-decomposition 352
Complete part of tree-decomposition 326
Complete r-partite graph 17
Complete separator 325 352
Complete subgraph 117 126—127 163—167 296 312 321
Complete topological minor 67—70 81 97 101 109 169—170 172 175 190 194
Complexity theory 127 341 356
Component 11 229 361
Connected 10
Connected and vertex enumeration 10 14
Connected, 2-connected graphs 55—57 78 89 94 270 281
Connected, 3-connected graphs 57—62 78 89 96 97 102 269 270
Connected, 4-connected graphs 108 270 278
Connected, arc-connected 229 243 248
Connected, infinitely connected 197 237 244
Connected, k-connected 11 12 67 79
Connected, k-connected, externally 329 352
Connected, minimally connected 14
Connected, minimally k-connected 80
Connected, semiconnected 535—236
Connected, topologically 229
Connectedness 10 14
Connectivity 11 10—13 55—81
Connectivity and average degree 12
Connectivity and chromatic number 116—117
Connectivity and circumference 79
Connectivity and edge-connectivity 12
Connectivity and girth 237 301
Connectivity and Hamilton cycles 277—278
Connectivity and linkability 70—71 80 81
Connectivity and minimum degree 12 249
Connectivity and plane duality 108
Connectivity and plane representation 96
Connectivity and Ramsey properties 268—270
Connectivity in infinite graphs 216—226
Connectivity in infinite graphs, forcing minors 354
Connectivity of a random graph 303
Connectivity via spanning trees 46 54
Connectivity, external 325 329 352 353 390
CONTAINS 3
Continuum many 357
Contraction 18—21
Contraction and 3-connectedness 58—59
Contraction and minors 18—21
Contraction and tree-width 320 321
Contraction in multigraphs 28—30 160
Convex drawing 99 107 109 386
Convex polygon 271
Core 376
Corneil, D.G. 355
Cornuejols, G. 138
Countable graph 2
Countable set 357
Countably infinite 357
Cover by antichains 53
Cover by chains 51
Cover by edges 136
Cover by paths 49—51 223
Cover by trees 49 106 250
Cover by vertices 33 34—35 44—46 322 338
Cover of a bramble 322
Critical 134
Critically k-chromatic 134 375 380
Cross-edges 24 46 235
Crosscap 362 364
Crosses in grid 322
Crown 269—270
Cube of a graph, 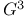 290 290
Cube, d-dimensional 30 313
Cubic graph 5
Cubic graph, 1-factor in 41 52
Cubic graph, connectivity of 79
Cubic graph, flow number of 150 151 157 161 162
Cubic graph, multigraph 44 52 157 282
Cuff 339
Curran, S. 54
Cut 24
Cut in network 142
Cut, capacity of 142 143
Cut, even/odd 233 243 244 249
Cut, flow across 141
Cut, fundamental 26 32 231 243
Cut, minimal 25 31 56 104
Cut, space 25—28 31 32 101 105 249
Cut-cycle duality 104—106 152—154
Cut-edge see bridge
Cutvertex 11 55—56
CYCLE 7—8
Cycle in multigraphs 29
Cycle space 23—28 31 32 59—62 101—102 105 107 109 232—235 243 244 248 249 374
Cycle space, topological 232—235 248 249
Cycle threshold function 311 313
Cycle with orientation 152—154
Cycle, directed 134 135
Cycle, disjoint cycles 44—45
Cycle, double cover conjecture 157 160
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -system
-system  -regular pair
-regular pair 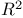
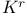 -subgraphs
-subgraphs