|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph theory |
|
|
 |
| Предметный указатель |
Thomas, R. 53 71 81 128 137 138 162 175 193 269 270 273 291 322 325 340 341 354 355 356
Thomason, A.G. 170 192 305
Thomasse, S. 246
Thomassen, C. 80 109 122 137 138 171 193 244 247 291 355 356 365
Three colour theorem 113
Three-flow conjecture 157
Threshold function 305—312 313 314
Toft, B. 136 162
Topological connectedness 229 236
Topological cycle space 232—235 248 249
Topological edge 226
Topological end degree 229
Topological end space 226—237 242
Topological Euler tour 244
Topological forest 250
Topological isomorphism 93 94 104
Topological minor 20
Topological minor and planarity 92 96—101
Topological minor and WQO of general graphs 350
Topological minor and WQO of trees 317
Topological minor as order relation 20
Topological minor of all large 2-connected graphs 269
Topological minor vs. ordinary minor 20 97
Topological minor, 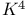 59 173—174 191 327 59 173—174 191 327
Topological minor, 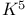 92 97 100 101 109 174 193 352 92 97 100 101 109 174 193 352
Topological minor, 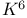 and and 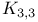 92 97 100 101 107 109 92 97 100 101 107 109
Topological minor, 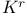 70 165 169—172 175 190 191 193—194 252 268 340 70 165 169—172 175 190 191 193—194 252 268 340
Topological minor,  197 205 238 241 341 354 197 205 238 241 341 354
Topological minor, 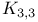 92 97 100 101 109 191 92 97 100 101 109 191
Topological minor, forced by average degree 70 169—172
Topological minor, forced by chromatic number 175
Topological minor, forced by girth 172 175
Topological minor, induced 170
Topological minor, tree (induced) 169
Topological spanning tree 49 231—237 242 243 250 385
Torso 339—311
Total chromatic number 135
Total colouring 135
Total colouring, conjecture 135 138
Total value of a flow 142
Touching sets 322
Toughness conjecture 218 289 290 291
Tournament 289
Transflnite induction 198—199 359
Transitive graph 52
Travelling salesman problem 290
TREE 13—16
Tree as forced substructure 15 169 190
Tree cover 46—49
Tree, binary 203 238
Tree, infinite 205 228 232 239 242 245 341 356
Tree, level of 15
Tree, normal 15—16 31 155 160 389
Tree, path-width of 352
Tree, spanning 14 16 198 205
Tree, spanning, topological 49 231—237 242 243 250 385
Tree, threshold function for 312
Tree, well-quasi-ordering of trees 317—318
Tree-decomposition 193 319—326 340 341 351 354—355
Tree-decomposition obstructions 322—324 328—329 354 355
Tree-decomposition, induced on minors 320
Tree-decomposition, induced on subgraphs 320
Tree-decomposition, lean 325
Tree-decomposition, part of 319
Tree-decomposition, simplicial 325 339 352 355
Tree-decomposition, width of 321
Tree-order 15
Tree-packing 46—48 52 53 235 249 250
Tree-packing theorem 46 235
Tree-width 321—341
Tree-width and brambles 322—324 353 355
Tree-width and forbidden minors 327—341
Tree-width of a minor 321
Tree-width of a subdivision 351
Tree-width of grid 324 351 354
Tree-width, compactness theorem 354
Tree-width, duality theorem 322—324
Tree-width, finite 341
Tree-width, obstructions to small 322—324 328—329 354 355
triangle 3
Triangulated see chordai
| Triangulation see plane triangulation
Trivial graph 2
Trotter, W.T. 256 272
Turan graph 165—169 192 379
Turan theorem 165 192 256
Turan, P. 165
Tutte 1-factor theorem 39 53 225
Tutte condition 39—40
Tutte cycle basis theorem 59 249
Tutte decomposition of 2-connected graphs into 3-connected pieces 57
Tutte flow conjectures 156—151 162
Tutte planarity criterion 102 109
Tutte polynomial 162
Tutte tree-packing theorem 46 53—54 235 250
Tutte wheel theorem 58—59 80
Tutte, W.T. 39 46 53 57 58 59 80 102 109 144 147 155 161—162 225 235 250 218 291
Tychonoff's theorem 201 245 381
Ubiquitous 201 240 246
Ubiquitous conjecture 201 240 246
Unbalanced subgraph 312 313 314
Unfriendly partition conjecture 202 245
Uniformity lemma see regularity lemma
union 3
Unit circle 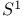 84 361 84 361
Universal graphs 212—216 213 240 246
Unmatched 33
Up (-closure) 15
Upper bound 358
Upper density 189
Urquhart, A. 137
Valency (degree) 5
Value of a flow 142
Variance 307
Veldman, H.J. 291
Vella, A. 249
Vertex 2
Vertex cover 34 49—51
Vertex cut see separator
Vertex duplication 166
Vertex expansion 129
Vertex of a plane graph 86
Vertex space 23
Vertex, colouring 111 114—118
Vertex-chromatic number 111
Vertex-connectivity 11
Vertex-transitive 52 215 239
Vince, A. 314
Vizing, V.G. 119 137 138 376 377 380
Voigt, M. 137—138
Vortex 340 353
Vuskovic, K. 138
Wagner graph 174 325—326 352
Wagner, K. 101 109 174 190 191 193 354—355
Walk 10
Walk length 10
Walk, alternating 64
Walk, closed 10
Wave 217 241
Wave limit 218
Wave, large 218
Wave, maximal 218
Wave, proper 218
Wave, small 218
Weakly perfect 226 242
Well-founded set 358
Well-ordering 358 386
Well-ordering theorem 358
Well-quasi-ordering 316—356
Welsh, D.J.A. 162
Wheel 59 270
Wheel theorem 58—59 80
Whitney, H. 81 96 105
Width of tree-decomposition 321
Wilson, R.J. 32
Winkler, P. 314
Wollan, P. 71 81
Woodrow, R.E. 215 246
Yu, X. 54 291
Zehavi, A. 54
Zorn's lemma 198 237 360
Zykov, A.A. 192
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



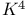
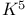
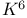 and
and