|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. Ч Graph theory |
|
|
 |
| ѕредметный указатель |
Cycle, edge-disjoint cycles 190 240 271
Cycle, expected number 298
Cycle, facial 101
Cycle, fundamental 26 32 382
Cycle, Hamilton 160 275Ч291
Cycle, Hamilton, infinite 278 289
Cycle, induced 8 23 59 89 102 127 128 243 376 380 385
Cycle, infinite 106 230Ч231 249 278
Cycle, length 8
Cycle, long 8 30 79 134
Cycle, non-separating 59 89 102 243 385
Cycle, odd 17 115 128 370 376
Cycle, short 10 117 171Ч172 299Ч301
Cycle-bond duality 104Ч106 152Ч154
Cyclomatic number 23
Cylinder 362
Czipszer, J. 249
de Bruijn, N.G. 201 245
Dean, N. 291
Degeneracy see coiouring number
Degree 5
Degree at a loop 29
Degree of an end 204 %%9 231 248
Degree, sequence 278
Deletion 4
Dense graphs 164 167
Dense linear order 241
Density of pair of vertex sets 176
Density, edge density 164
Density, upper density 189
Depth-first search tree 16 31
Deuber, W. 258 273
Diameter 8Ч9 312
Diameter and girth 8
Diameter and radius 9
Diestel, R. 110 193 216 228 233 235 244Ч250 291 340 341 355 356
Difference of graphs 4 86
Digon see double edge
Digraph see directed graph
Dilworth, R.P. 51 53 241 372 386
Dirac, G.A. 194 276
Directed cycle 134 135
Directed edge 28
Directed graph 28 49Ч50 124 135 246 376
Directed path 49 134 375 376
Direction 140
Disc 361
Disconnected 10
Disjoint graphs 3
Dispersed 239
Distance 8
Dominated 238 249
Double counting 91 109 130Ч131 298 309
Double edge 29 103
Double ray 196 240 250 291
Double wheel 269Ч270
Down (-closure) 15
Drawing 2 83 92Ч96 381
Drawing convex 99 109
Drawing straight-line 99 107
Dual abstract 105Ч106 108
Dual and connectivity 108
Dual plane 103Ч105 108
Duality cycles and bonds 26Ч28 104Ч106 152
Duality flows and colourings 152Ч155 378
Duality for infinite graphs 106 109 110
Duality of plane multigraphs 103Ч106
Duality tree-decompositions and brambles 322
Duplicating a vertex 129 166
EDGE 2
Edge colouring 112 119Ч121 253 259
Edge colouring and flow number 151
Edge colouring and matchings 135
Edge contraction 18
Edge contraction and 3-connectedness 58
Edge contraction in multigraph 29
Edge contraction vs. minors 19
Edge cover 136
Edge density 5 6 164
Edge density and average degree 5
Edge density and regularity lemma 176 191
Edge density, forcing minors 170
Edge density, forcing path linkages 71Ч77
Edge density, forcing subgraphs 164Ч169
Edge density, forcing topological minors 70 169
Edge of a multigraph 28
Edge plane 86
Edge space 23 31 101 232
Edge, crossing a partition 24
Edge, directed 28
Edge, double 29
Edge, space 23
Edge, topological 226
Edge, X-Y edge 2
Edge-chromatic number see chromatic index
Edge-connectivity 12 46 67 79 134 150 197
Edge-disjoint spanning trees 46Ч49 52 197
Edge-maximal 4
Edge-maximal vs. extremal 165 173
Edge-maximal without  174 174
Edge-maximal without  173 173
Edge-maximal without  , ,  100 100
Edge-maximal without  191 191
Edmonds, J. 53 225 356
Embedding in 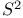 85Ч86 93 85Ч86 93
Embedding in surface 91 109 341Ч349 353 356 363
Embedding in the plane 92 95Ч110
Embedding k-near embedding 340
Embedding of bipartite graphs 263Ч265
Embedding of graphs 21
Embedding, self-embedding 349
Empty graph 2 11
End degree 204 229 231 248
End degree in subspaces 229 231 248Ч249
End of edge 2 28
End of graph 49 106 195 202Ч203 204Ч212 226Ч244 248Ч249
End of path 6
End of topological space 242
End space 226Ч237 242
End, thick/thin 208Ч212 238
End-faithful spanning tree 242
Endpoints of arc 84 229
Endvertex 2 28
Endvertex, terminal vertex 28
Enumeration 357
Equivalence in definition of an end 202 242
Equivalence in quasi-order 350
Equivalence of graph invariants 190
Equivalence of graph properties 270
Equivalence of planar embeddings 92Ч96 106 107
Equivalence of points in topological space 84 361
Erdoes Ч Menger conjecture 217 247
Erdoes Ч Posa property 44 52 338Ч339 353
Erdoes Ч Posa theorem 45 53
Erdoes Ч Posa theorem, edge version 190 271
Erdoes Ч Posa theorem, generalization 338Ч339
Erdoes Ч Sos conjecture 169 189Ч190 193
Erdoes Ч Stone theorem 164 167Ч168 186Ч187 193
Erdoes, P. 45 53 117 137 167 169 185 192 193 194 201 213 216 217 244 245 246Ч247 249 250 258 271 272 273 277 291 293Ч294 296 299Ч301 306 308 314 387
Euler characteristic 363
Euler formula 91Ч92 106 363 376
Euler genus 343 363Ч366
Euler tour 22 244 378 385
Euler, L. 22 32 91
Eulerian graph 22
Eulerian graph, infinite 233 244 248 249Ч250
Even degree 22 39
Even graph 150 151 161 248
Event 295
Evolution of random graphs 305 313 314
| Exceptional set 176
Excluded minors see forbidden minors
Existence proof, probabilistic 137 293 297 299Ч301
Expanding a vertex 129
Expectation 297Ч298 307
Exterior face see outer face
External connectivity 329 352 353
Extremal bipartite graph 189
Extremal graph 164Ч166
Extremal graph theory 163Ч194 248Ч249
Extremal vs. edge-maximal 164Ч165 173
Extremal without  174 174
Extremal without  173 173
Extremal without  191 191
Face 86 363
Face of hexagonal grid 342
Face, central face 342
Facial cycle 101
Factor 33
Factor, 1-factor 33Ч43 52 216Ч226 238 241
Factor, 1-factor theorem 39 41 52 53 80 81 225 247
Factor, 2-factor 39
Factor, k-factor 33
Factor-critical 41 225 242 371 384
Fajtlowicz, S. 193
Fan 66 238
Fan-version of Menger's theorem 66 238
Finite adhesion 340 341
Finite graph 2
Finite intersection property 201
Finite set 357
Finite tree-width 341
First order sentence 303 314
First point on frontier 84
Five colour theorem 112 137 157
Five colour theorem, list version 122 138
Five-flow conjecture 156 157 162
Fleischner, H. 281 289 291 387
Flow 139Ч162 141Ч142
Flow conjectures 156Ч157 161 162
Flow in plane graphs 152Ч155
Flow integral 142 144
Flow network flow 141Ч144 160 161 378
Flow number 147Ч151 156 160 161
Flow polynomial 146 149 162
Flow, 2-flow 149
Flow, 3-flow 150 157 161
Flow, 4-flow 150Ч151 156Ч157 160 161 162
Flow, 6-flow theorem 157Ч159 161 162
Flow, group-valued 144Ч149 160 161Ч162
Flow, H-flow 144Ч149 160
Flow, k-flow 147Ч151 156Ч159 160 161 162
Flow, total value of 142
Flow-colouring duality 152Ч155 378
Forbidden minors and chromatic number 172Ч175
Forbidden minors and tree-width 327Ч341
Forbidden minors in infinite graphs 216 244 245 340Ч341
Forbidden minors, expressed by 327 340Ч349
Forbidden minors, minimal set of 341 352 355
Forbidden minors, planar 328
Forcibly hamiltonian see hamiltonian sequence
Forcing 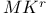 169Ч175 192Ч194 340 353 169Ч175 192Ч194 340 353
Forcing  341 354 341 354
Forcing  174 193 174 193
Forcing  70 169Ч170 172 175 193Ч194 70 169Ч170 172 175 193Ч194
Forcing edge-disjoint spanning trees 46
Forcing Hamilton cycles 276Ч278 281 289
Forcing high connectivity 12
Forcing induced trees 169
Forcing large chromatic number 117Ч118
Forcing linkability 70Ч72 81
Forcing long cycles 8 30 79 134 275Ч291
Forcing long paths 8 30
Forcing minor with large minimum degree 171 193
Forcing short cycles 10 171Ч172 175 301
Forcing subgraph 15 163Ч169 175Ч194
Forcing tree 15 169
Forcing triangle 135 271
Ford, L.R.Jr. 143 161
Forest 13 173 327
Forest, minor 355
Forest, partitions 48Ч49 53 250
Forest, plane 88 106
Forest, topological 250
Forest, tree-width of 327 351
Four colour problem 137 193
Four colour theorem 112 157 161 172 174 191 278 290
Four colour theorem, history 137
Four-flow conjecture 156Ч157
Fraisse, R. 246
Frank, A. 80 161
Freudenthal compactification 227 248
Freudenthal ends 242
Freudenthal, H. 248
Frobenius, F.G. 53
From 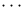 to 6 to 6
Frontier 84 361
Fulkerson, D.R. 122 143 161
Fundamental circuit 231 233 243
Fundamental cocycle 26 32
Fundamental cut 26 32 231 243
Fundamental cycle 26 32
Gale, D. 38
Gallai Ч Edmonds matching theorem 41Ч43 53 225 247
Gallai, T. 32 43 50 52 53 54 81 192 238 249
Galvin, F. 125 138
Gasparian, G.S. 129 138
Geelen, J. 356
GENERATED 233
Genus and colouring 137
Genus of a graph 106 353
Genus of a graph, orientable 353
Genus of a surface 348
Genus, Euler genus 343 363Ч366
Geometric dual see plane dual
Georgakopoulos, A. 248
Gibbons, A. 161
Gilmore, P.C. 136
girth 8
Girth and average degree 9Ч10 301
Girth and chromatic number 117 137 299Ч301
Girth and connectivity 81 237 301
Girth and diameter 8
Girth and minimum degree 8 10 30 171 301
Girth and minors 170Ч172 191 193
Girth and planarity 106 237
Girth and topological minors 172 175
Godsil, C. 32
Goering, F. 81
Golumbic, M.C. 138
Good characterization 341 356
Good pair 316 347
Good sequence 316
Gorbunov, K.Yu. 355
Graham, R.L. 272
Graph 2Ч4 28 30
Graph, homogeneous 215 240 246
Graph, invariant 3 30 190 297
Graph, minor theorem 315 341Ч348 342 349 354 355
Graph, minor theorem, for trees 317Ч318
Graph, partition 48
Graph, plane 86Ч92 103Ч106 112Ч113 122Ч124 152Ч155
Graph, process 314
Graph, property 3 212 270 302 312 327 342 356
Graph, simple 30
Graph, universal 212Ч216 213 240 246
Graph-theoretical isomorphism 93Ч94
Graphic sequence see degree sequence
Greedy algorithm 114 124 133
grid 107 208 322
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте





 ,
, 
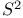


 to
to