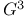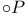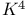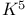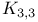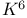|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph theory |
|
|
 |
| Предметный указатель |
Grid, canonical subgrid 342
Grid, hexagonal grid 208 209 342—346
Grid, minor 240 324 328—338 354
Grid, theorem 328
Grid, tree-width of 324 351 354
Groetzsch, H. 113 137 157 161
Group-valued flow 144—149 160 161—162
Gruenwald, T. see Gallai
Gusfleld, D. 53
Guthrie, F. 137
Gyarfas, A. 169 190 194
Hadwiger conjecture 172—115 191 193
Hadwiger, H. 172 193
Hajnal, A. 244 245 249 250 258 272 273
Hajos conjecture 175 193
Hajos construction 117—118
Hajos, G. 118 137 175
Haken, W. 137
Halin, R. 80 206 208 244 245—246 354—355 356
Hall, P. 36 51 53 224
Hamilton circle 278 289 291
Hamilton cycle 275—291
Hamilton cycle and 4-flows 160 278
Hamilton cycle and degree sequence 278—281 289
Hamilton cycle and minimum degree 276
Hamilton cycle and the four colour theorem 278
Hamilton cycle in  281—289 281—289
Hamilton cycle in 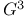 290 290
Hamilton cycle in almost all graphs 305
Hamilton cycle in infinite graph see Hamilton circle
Hamilton cycle in planar graphs 278
Hamilton cycle, power of 289
Hamilton cycle, sufficient conditions 275—281
Hamilton path 275 280—281 289 290
Hamilton, W.R. 290
Hamiltonian graph 275
Hamiltonian sequence 279
Handle 362 364
Harant, J. 81
head see terminal vertex
Heawood, P.J. 137 161
Heesch, H. 137
Height 15
Hexagonal grid 208 209 342—346
Higman, D.G. 316 354
Hoffman, A.J. 136
hole 138
Holz, M. 247
Homogeneous graphs 215 240 246
Hoory, S. 10 32
Huck, A. 244
Hypergraph 28
incidence 2
Incidence map 29
Incidence matrix 27
Incidence, encoding of planar embedding see combinatorial isomorphism
incident 2 88
Incomparability graph 242
Increasing property 305 313
Independence number 126—133
Independence number and connectivity 276—277
Independence number and covers 50 52
Independence number and Hamilton cycles 276—277
Independence number and long cycles 134
Independence number and perfection 132
Independence number of random graph 296 312
Independent edges 3 33—43 52
Independent events 295
Independent paths 7 66—67 677—669 370
Independent vertices 3 50 124 296
Indicator random variable 298 387
Induced subgraph 3—4 68 126 128 132 376
Induced subgraph in Ramsey theory 252 258—268 271
Induced subgraph in random graph 296 313
Induced subgraph of all imperfect graphs 129 135
Induced subgraph of all large connected graphs 268
Induced subgraph of almost all graphs 302 313
Induced subgraph tree 169 190
Induced subgraph, cycle 8 23 31 59 89 102 127 128 249 376 380 385
Induction, transfinite 198—199 359
Induction, Zorn's Lemma 198 237 360
Inductive ordering 199
Infinite graphs 2 19 31 51 110 189 195—250 253 278 289 291 305—306 340—341 349 354 356
Infinite sequence of steps 197 206
Infinite set 357
Infinite set, basic properties 197—198
Infinitely connected 197 237 244
Infinity lemma 200 245 383
Initial segment 358
Initial vertex 28
Inner face 86
Inner point 226
Inner vertex 6
Integral, flow 142 144
Integral, function 142
Interior of a path, 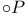 6—7 6—7
Interior of an arc 84
Internally disjoint see independent
Intersection 3
Intersection graph 352
Interval graph 127 136 352
INTO 319
Invariant 3
Irreducible graph 352
Irving, R.W. 53
Isolated vertex 5 313
Isomorphic 3
Isomorphism 3
Isomorphism of plane graphs 92—96
Isthmus see bridge
Itai, A. 54
Jaeger, F. 162
Janson, S. 313
Jensen, T.R. 136 162 355
Johnson, D. 356
Join 2
Jonsson, B. 246
Jordan curve theorem 84 109
Jordan, C. 84 86
Jung, H.A. 70 194 205 239 245
k-choosable 121
k-colourable 111 121 201 325
k-constructible 117—118 134 137
k-list-colourable see k-choosable
k-mesh 329
k-near embedding 340
Kahn, J. 138
Karoriski, M. 314
Kawarabayashi, K. 193
Kelmans, A.K. 102 109—110
Kempe, A.B. 137 290
Kernel of directed graph 124 135
Kernel of incidence matrix 27
Kirchhoff's law 139 140
Klein four-group 151
Kleitman, D.J. 137
Knot theory 162
Knotless graph 349
Kochol, M. 149 162
Koenig, D. 35 53 119 200 245
Koenig, duality theorem 35 49 51 52 63 127 136 223
Koenig, infinity lemma 200 245
Koenigsberg bridges 21
Kohayakawa, Y. 194
Kollar, J. 192
Komlos, J. 192 194 272 289 291
Korman, V. 226
Kostochka, A.V. 170 192 273
Kriesell 53
Kruskal, J.A. 317 354 389
| Kuehn, D. 81 172 175 193 194 216 233 246—250
Kuratowski -type characterization 107 270 341—342 355—356
Kuratowski set of graph properties 270
Kuratowski set of graphs 341—342 355
Kuratowski, C. 96—101 109 238 249 356
Kuratowski-theorem for higher surfaces 342
l-edge-connected 12
Lachlan, A.H. 215 246
Large wave 218
Larman, D.G. 70
Latin square 135
Laviolette, F. 250
Leader, I.B. 245 246
Leaf 13 15 31 204
Lean tree-decomposition 325
Lee, O. 54
Length of a cycle 8
Length of a path 6 8
Length of a walk 10
Level 15
LIMIT 199—200 358
Limit wave 218
Line (edge) 2
Line (edge) graph 4 112 136 191
Line (edge) segment 84
Linear algebra 23—28 59—61 101—102 132
Linear decomposition 339—340
Linear programming 161
Linial, N. 10 32
Linkable 219
Linked by a path 6
Linked by an arc 84
Linked k-linked 69—77 80 81 170
Linked k-linked vs. k-connected 69—71 80 81
Linked tree-decomposition 325
Linked vertices 6 84
List colouring 121—126 137—138
List colouring, bipartite graphs 124—126 135
List colouring, Brooks's theorem 137
List colouring, conjecture 124 135 138
List-chromatic index 121 124—126 135 138
List-chromatic number see choice number
Liu, X. 138
Lloyd, E.K. 32
Locally finite 196 248 249
Logarithms 1
Loop 28
Lovasz, L. 53 129 132 137 138 192
Luczak, T. 313 314
MacLane, S. 101 109—110
Mader, W. 12 32 67—69 80 81 170 190 192 193 355
Magnanti, T.L. 161
Maharry, J. 193
Mani, P. 70
Map colouring 111—113 133 136 152
Markov chain 314
Markov's inequality 297 301 307 309
Marriage theorem 35—36 39 51 53 223—224 238 371
Marriage theorem, stable 38 53 126 383
Matchable 41 223
Matching 33—54
Matching and edge colouring 135
Matching in bipartite graphs 34—39 127
Matching in general graphs 39—43
Matching in infinite graphs 222—226 241—242 247—248
Matching in infinite graphs, partial 224 241
Matching of vertex set 33
Matching, stable 38 51 52 126
Mate, A. 250 272
Matroid theory 54 110 356
Max-flow min-cut theorem 141 143 160 161
Maximal 4
Maximal acyclic graph 14
Maximal element 358 360
Maximal planar graph 96 101 107 109 174 191 374
Maximal plane graph 90 96
Maximal wave 218
Maximum degree 5
Maximum degree and chromatic index 119—121
Maximum degree and chromatic number 115
Maximum degree and list-chromatic index 126 138
Maximum degree and radius 9
Maximum degree and Ramsey numbers 256—257
Maximum degree and total chromatic number 135
Maximum degree, bounded 184 256
Menger, K. 53 62—67 79 81 160 206 216—226 241 246—247
Menger, theorem of 62—67 79 81 160 206—207 216 217 238 246—247
Metrizable 228 242
Milgram, A.N. 50 52 53 54
Milner, E.C. 245
Minimal 4
Minimal cut 25 31 56 104 152
Minimal element 358
Minimal non-planar graph 107
Minimal separator 78
Minimal set of forbidden minors 341 353 355—356
Minimal, connected graph 14
Minimal, k-connected graph 80
Minimum degree 5
Minimum degree and average degree 5
Minimum degree and choice number 121—122
Minimum degree and chromatic number 115 116—117
Minimum degree and circumference 8
Minimum degree and connectivity 12 80 249
Minimum degree and edge-connectivity 12
Minimum degree and girth 8 9 10 170—172 193 301
Minimum degree and linkability 71
Minimum degree, forcing Hamilton cycle 276 289
Minimum degree, forcing long cycles 8
Minimum degree, forcing long paths 8 30
Minimum degree, forcing short cycles 10 171—172 175 301
Minimum degree, forcing trees 15
Minor 18—21 20 169—172
Minor and planarity 96—101 107
Minor and WQO 315—356 (see also topological minor)
Minor of all large 3- or 4-connected graphs 269—270
Minor of multigraph 29
Minor Petersen graph 156
Minor relation 20 31 207 216 240 246 270 321 342
Minor theorem 315 341—349 342 354—355
Minor theorem for trees 317—318
Minor theorem, proof 342—348
Minor vs. topological minor 20—21 97
Minor, 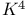 173 327 173 327
Minor, 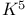 174 193 352 174 193 352
Minor, 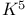 and and 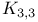 96—101 96—101
Minor, 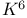 175 175
Minor, 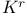 170 171 172 190 191 193—194 313 340 353 354 170 171 172 190 191 193—194 313 340 353 354
Minor, 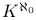 341 354 341 354
Minor, 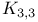 109 191 109 191
Minor, excluded see forbidden
Minor, forbidden 172—175 216 244 327—349 352 354—356
Minor, forced 171 172 169—175
Minor, incomplete 192
Minor, infinite 197 207—208 216 240 244 245 246 248—249 354 356
Minor, proper 349
Minor-closed graph property 327 341—349 352
Moebius crown 269—270
Moebius ladder 174
Moebius strip 362
Mohar, B. 109 137 193 356
Moment, first see Markov's inequality
Moment, second 306—312
Monochromatic (in Ramsey theory), (vertex) set 253—255
Monochromatic (in Ramsey theory), induced subgraph 257—268
Monochromatic (in Ramsey theory), subgraph 253 255—257
Moore bound 10 32
Multigraph 28—30
Multigraph, cubic 44 52 157 282
Multigraph, list chromatic index of 138
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте