|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph theory |
|
|
 |
| Предметный указатель |
Multigraph, plane 103
Multiple edge 28
Multiplicity 248
Murty, U.S.R. 291
Myers, J.S. 192
Nash — Williams, C.St.J.A. 46 49 53 235 244 246 247 249—250 291 354
Nearly planar 340 341
Negropontis, S. 250
Neighbour of a set of vertices 5
Neighbour of a vertex 3
Nesetfil, J. 272 273
Network 141—111
Network theory 161
Niedermeyer, F. 244 248
Node (vertex) 2
Normal ray 205 239 384
Normal tree 15—16 31 155 160 271 389
Normal tree in infinite graphs 205 228 232 239 242 245 341 356
Nowhere dense 49
Nowhere zero 144 162
NULL see empty
Obstruction to small tree-width 322—324 328—329 354 355
octahedron 12 17 355
Odd component 39 238
Odd cycle 17 115 128 135 138 370 376
Odd degree 5 290 387
ON 2
One-factor theorem 39 53 81 225
Open Euler tour 244
Oporowski, B. 269 270 273 354
Order of a bramble 322
Order of a graph 2
Order of a mesh or premesh 329
Order of a separation 11
Order, partial 15 20 31 50—51 53 136 350 357 358 360
Order, quasi- 316
Order, tree- 15 31
Order, type 358
Order, well-quasi- 315—317 342 350 354
Ordinal 358—359
Orientable surface 353
Orientable surface, plane as 153
Orientation 28 124 134 161 190 376
Orientation, cycle with 152—153
Oriented graph 28 289
Orlin, J.B. 161
Osthus, D. 81 172 175 193 194
Outer face 86 93—94 107
Outerplanar 107
Oxley, J.G. 93 110 250 269 270 273
Oxtoby, J.C. 250
Packing 33 44—49 52 235 250
Palmer, E.M. 313
Parallel edges 29
Parity 5 39 42 290
Part of tree-decomposition 319
Partially ordered set 50—51 53 241 358 360
Partition 1 48 253
Pasting 127 173 174 191 325 352
Path 6—10 196
Path between given pairs of vertices 69—77
Path cover 49—51 50 223 372
Path, -connected 248 384
Path, a-b-path 7 66
Path, alternating 34—35 37 63
Path, directed 49
Path, disjoint paths 50 62—67 69—77 217—222
Path, edge-disjoint 46 66—67 68—69
Path, H-path 7 57 67—69 79 80 81
Path, independent paths 7 66—67 67—69 79 80 370
Path, induced 270
Path, length 6
Path, linkage 69—77 81 373
Path, long 8
Path-decomposition 339 352
Path-hamiltonian sequence 280—281
Path-width 352 355
Perfect 126—133 135—136 137—138 226
Perfect graph conjectures 128
Perfect graph theorems 128 129 135 138
Perfect matching see J-factor
Perfect, strongly 226 242
Perfect, weakly 226 242
Petersen graph 156—157
Petersen, J. 39 41
Piecewise linear 83
Planar 96—110 112—113 122 216 328 338 341
Planar, embedding 92 96—110
Planar, nearly planar 340 341
Planarity criteria, Kelmans 102
Planarity criteria, Kuratowski 101
Planarity criteria, MacLane 101
Planarity criteria, Tutte 109
Planarity criteria, Whitney 105
Plane graph 86—92
Plane multigraph 103—106 108 152—155
Plane, dual 103
Plane, duality 103—106 108 152—155
Plane, triangulation 90 91 161 325
Plummer, M.D. 53
Podewski, K.P. 247 248
Point (vertex) 2
Pointwise greater 279
Polat, N. 248
Polygon 84
Polygonal arc 84 85
Posa, L. 45 53 258 273
Power of a graph 281
Power set 357
Predecessor 358
Preferences 38 51 126
Premesh 329
Prikry, K. 245
Probabilistic method 293 299—302 314
Projective plane 355
Proper minor 349
Proper separation 11
Proper subgraph 3
Proper wave 218
Property 3 270 302
Property of almost all graphs 302—306 311—312
Property, increasing 305
Property, minor-closed 327 352
Proskurowski, A. 355
Pseudo-random graph 272
Pym, J.S. 223 247
Quasi-ordering 315—317 342 350 354
r-partite 17
RADIUS 9
Radius and diameter 9 30
Radius and maximum degree 9
Rado's selection lemma 245
Rado, graph 214—215 240 241 246 306
Rado, R. 245 246 250 272
Ramsey graph 258
Ramsey numbers 253 255 271 272—273 296 314
Ramsey theory 251—273
Ramsey theory and connectivity 268—270
Ramsey theory, induced 258—268
Ramsey theory, infinite 253—254 271 272
Ramsey, F.P. 252—255
Ramsey-minimal 257—258
Random graph 170 175 255 293—314 295
Random graph, evolution 305 311 314
Random graph, infinite 305—306
Random graph, process 314
Random graph, uniform model 314
Random variable 297
Random variable, indicator r.v. 298 387
Ray 196 200 204 206 239 240 242 341
| Ray, double 196 240 250 291
Ray, normal 205 239 384
Ray, spanning 291
Recursive definition 359—360
Reducible configuration 137
Reed, B.A. 53 355
Refining a partition 1 178—182
Region 84—86
Region on 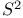 86 86
Regular 5 37 39 135 289
Regularity graph 184
Regularity graph, inflated, 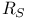 256 256
Regularity lemma 164 175—188 176 191 193—194 272
Renyi, A. 213 246 306 308 314
Richardson, M. 135
Richter, B. 356
Rigid-circuit see chordai
Riha, S. 291
Ring 342—343
Robertson, N. 53 128 137 138 162 175 193 321 328 340 341 342 354—355 356
Roedl, V. 194 256 258 272—273
Ronyai, L. 192
Root 15
Rooted tree 15 317 350
Rothschild, B.L. 272
Royle, G.F. 32
Rucinski, A. 313 314
Salazar, G. 356
Sanders, D.P. 137
Sarkozy, G.N. 289 291
Saturated see edge-maximal
Sauer, N. 246
Schelp, R.H. 210
Schoenflies, A.M. 86
Schrijver, A. 53 80 81 138 161
Schur, I. 271
Scott, A.D. 194 246
Second moment 306—312 307
Self-minor conjecture 349 353 354
Semiconnected 535—236
Separate a graph 11 62 66 67
Separate the plane 84
Separating circle 362 365
Separation 11
Separation and tree-decompositions 320 351 353
Separation, compatible 351
Separation, order of 11
Separator 11
Sequential colouring see greedy algorithm
Series-parallel 191
Set system see hypergraph
Set, countable 357
Set, countably infinite 357
Set, finite 357
Set, infinite 357
Set, k-set 1
Set, power set 357
Set, well-founded 358
Seymour, P.D. 53 128 137 138 157 162 175 193 289 291 321 322 328 340 341 342 349 354 355 356
Shapley, L.S. 38
Shelah, S. 244 245 246 247
Shi, N. 246
Shift-graph 271
Simonovits, M. 53 192 194 272
Simple basis 101 109
Simple graph 30
Simplicial tree-decomposition 244 325 352 355
Six-flow theorem 157 162
Small wave 218
Snark 157
Snark, planar 157 161 278
Sos, V. 169 189 190 192
Spanned subgraph 4
Spanning ray 291
Spanning subgraph 4
Spanning trees 14 16
Spanning trees, edge-disjoint 46—49
Spanning trees, end-faithful 242
Spanning trees, normal 15—16 31 205 228 232 239 242 245 341 356
Spanning trees, number of 313
Spanning trees, topological 49 231—237 242 243 250 385
Sparse graphs 163 169—172 191 194 255—256 273
Spencer, J.H. 272 314
Sperner's Lemma 51
Sphere 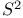 86 93—95 361 86 93—95 361
Spine 196
Spriissel, Ph. 32
Square of a graph 281—289 290 291
Square, Latin 135
Stability number see independence number
Stable marriage 38 53 126 383
Stable matching 38 51 52 126
Stable set 3
Standard basis 23
Standard subspace 227 231 236 243
Star 17 190 258 270
Star, centre of 17
Star, induced 268
Star, infinite 204
Star-comb lemma 204 205
Star-shape 374
Steffens, K. 224 247
Stein, M. 247 248 250
Steinitz, E. 109
Stereographic projection 85
Stillwell, J. 109
Stone, A.H. 167 183
Straight line segment 84
Strip neighbourhood 88 362
Strong core 376
Strongly perfect 226 242
Subcontraction see minor
Subdividing vertex 20
Subdivision 20
Subgraph 3
Subgraph of all large k-connected graphs 268—270
Subgraph of high connectivity 12
Subgraph of large minimum degree 6 115 134
Subgraph, forced by edge density 164—169 175— 189 190 191
Subgraph, induced 3
Subgraph, spanning 4
Successor 358
Sudakov, B. 273
Sum of edge sets 23
Sum of flows 149
Sum of thin families 232
Supergraph 3
Suppressing a vertex 29
surface 339 342 343 361—367
Surgery on 364
Surgery on surfaces 364
Surgery on surfaces, capping 364
Surgery on surfaces, cutting 364
Symmetric difference 23 34 64
System of distinct representatives 51
Szabo, T. 192
Szekeres, G. 271
Szemeredi, E. 176 192 194 256 272 289 291 see
t-tough 277—278 290
Tail of a ray 196 237
Tail of an edge see initial vertex
Tait, P.G. 137 290—291
Tangle 353 355
Tarsi, M. 137
Teeth 196
Terminal vertex 28
Thick/thin end 208—212 238
Thin end 208—212 238
Thin family 232
Thin sum 232
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте