Авторизация
Поиск по указателям
Grünbaum B. — Convex Polytopes
Обсудите книгу на научном форуме Нашли опечатку?
Название: Convex PolytopesАвтор: Grünbaum B. Аннотация: The appearance of Gruenbaum's book Convex Polytopes in 1967 was a moment of grace to geometers and combinatorialists. The special spirit of the book is very much alive even in those chapters where the book's immense influence made them quickly obsolete. Some other chapters promise beautiful unexplored land for future research. The appearance of the new edition is going to be another moment of grace. Kaibel, Klee and Ziegler were able to update the convex polytope saga in a clear, accurate, lively, and inspired way. —Gil Kalai, The Hebrew University of Jerusalem The original book of Gruenbaum has provided the central reference for work in this active area of mathematics for the past 35 years...I first consulted this book as a graduate student in 1967; yet, even today, I am surprised again and again by what I find there. It is an amazingly complete reference for work on this subject up to that time and continues to be a major influence on research to this day. —Louis J. Billera, Cornell University The original edition of Convex Polytopes inspired a whole generation of grateful workers in polytope theory. Without it, it is doubtful whether many of the subsequent advances in the subject would have been made. The many seeds it sowed have since grown into healthy trees, with vigorous branches and luxuriant foliage. It is good to see it in print once again. —Peter McMullen, University College LondonThe combinatorial study of convex polytopes is today an extremely active and healthy area of mathematical research, and the number and depth of its relationships to other parts of mathematics have grown astonishingly since Convex Polytopes was first published in 1966. The new edition contains the full text of the original and the addition of notes at the end of each chapter. The notes are intended to bridge the thirty five years of intensive research on polytopes that were to a large extent initiated, guided, motivated and fuelled by the first edition of Convex Polytopes. The new material provides a direct guide to more than 400 papers and books that have appeared since 1967. Branko Grünbaum is Professor of Mathematics at the University of Washington.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 2003Количество страниц: 466Добавлена в каталог: 30.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
see “ 199 225 228 213 217 235 354 354 355a 355b 296a see “Representation of a polytope” see “Representation of a polytope” 417 0/1-poly tope 69a 0/1-poly tope, Borsuk’s conjecture 423b 0/1-poly tope, Hirsch conjecture 355a 0/1-poly tope, maximal number of facets 69a 0/1-poly tope, random 69a 0/1-poly tope, simple 340a 120-cell 423b 24-cell 69a 423b 24-cell, f-vectors of 4-polytopes of type (2,2) 169 3-diagram see “Diagram” 3-polytope without triangles and quadrangles 198d 3-polytope, automorphisms and symmetries 296a 3-polytope, cutting off vertices 270 284 286 3-polytope, decompositions 340a 3-polytope, directed version of Steinitz’s theorem 296b 3-polytope, Eberhard’s theorem 296b 3-polytope, face vector 296b 3-polytope, Hamiltonicity 389a 3-polytope, inscribed in a sphere 296c 3-polytope, order dimension of the face lattice 296d 3-polytope, prescribing a shadow boundary 296b 3-polytope, prescribing the shape of a facet 296b 3-polytope, realization space 296b 3-polytope, realization with edges tangent to a sphere 296a 3-polytope, self-dual 52d 3-polytope, size of coordinates 296b 3-polytope, Steinitz’s theorem 296a 3-polytope, vertex vector 296b 3-polytopes, enumeration of see “Enumeration” 3-polytopes, number of see “Number” 3-realizable sequence 253 (see also “Eberhard’s theorem”) 3-realizable sequence, with 271 4-polytope, centrally symmetric, with 12 vertices 121b 4-polytope, coding sizes of coordinates 296d 4-polytope, complexity 198d 4-polytope, decompositions 340a 4-polytope, f-vectors 198d 4-polytope, fatness 198d 4-polytope, flag f-vectors 198c 4-polytope, Hamiltonicity 389a 4-polytope, non-rational 96a 4-polytope, universality theorem 96a 4-polytope, visualization 52c 4-polytopes, enumeration of see “Enumeration” 4-polytopes, number of see “Number” 4-realizable sequence 282 5-realizable sequence 271 600-cell 423b Abstract complex 206 Abstract scheme 91 Addition, Blaschke see “Blaschke sum” Addition, Minkowski 316 Addition, vector 9 38 316 Adjoining polytopes 83 Adjoint transformation 50 75 Admissible pair of numbers 352 Affine automorphism 77 Affine combination 2 Affine convex geometry 30b Affine dependence 2 85 Affine equivalence 5 74 89 Affine Gale-diagram 96a Affine hull 3 Affine transformation 4 9 Affine transformation, piecewise 41 Affine variety 3 Affinely regular polytope 412 Algebraic geometry 198c Algebraic numbers 96b Algebraic shifting 198c Algebraic shifting, generalized lower bound theorem 198b Algebraic variety, topological complexity 121a Algebraic variety, toric see “Toric variety” Almost-neighborly set 126 Ambiguity 225 Ambiguity, dimensional 225 Ambiguity, strong d-ambiguity 225 Ambiguity, weak d-ambiguity 226 Analogous polytopes 52c angle 297 Angle, external 308 Angle-sum 297 Angle-sums relations, cubical polytopes 313 Angle-sums relations, simplices 304 Angle-sums relations, simplicial polytopes 307 Antipodal, k-antipodal, pair 421 Antipodal, pair 420 Antipodal, polytope 420 Antipodal, strictly, subset of 128 Antiprism 66 215 Antistar 40 Apex of a cone 9 23 Apex of a pyramid 54 Approximation of polytopes 326 Archimedean solid 413 Area function 339 Arrangement of pseudo-lines 408 Arrangement, equivalence 394 Arrangement, f-vectors 399 Arrangement, generalized 407 Arrangement, index of a simple 2-arrangement 394 Arrangement, simple 391 Arrangement, spherical 409 Arrangement, stretchable 408 Arrangements, nonsimple 2-arrangement 396 Associated cone 49 Balinski’s theorem 213 Balinski’s theorem, directed version 224a Ball 5 Barnette sphere 224a Barycenter 315a Basic face of a Schlegel diagram 43 Basic variable 378 Basis of a pyramid 54 Bending facets 296a Beneath 78 Beneath-beyond method 96b Beyond 78 Bimatrix game 423c Bipyramid 55 Bipyramid, r-fold 55 Bipyramids, indecomposability of r-fold 323 Bipyramids, r-fold, and pyramidoids 64 Blaschke diagram 417 Blaschke sum 333 340c Blaschke’s selection theorem 10 325 Block 255 Borsuk — Ulam theorem 201 210 224a Borsuk’s problem 418 423b 423c Boundary complex 40 199 Boundary complex, Eulerian manifolds 141 Boundary complex, refinements of simplex skeleta 200 Boundary of a set 6 Boundary-free complex 50 Bounded d-step conjecture see “d-step conjecture” Bounded Hirsch conjecture see “Hirsch conjecture” Bounded set 5 23 Brueckner sphere 224a Bruggesser — Mani shelling see “Line shelling” Brunn — Minkowski theorem 338 Brunn — Minkowski theory 340c Caratheodory’s theorem 15 Cauchy sequence 5 Cauchy’s Rigidity Theorem 411 cd-index 198a 198c CDD 52b Cell complex 51 Cell of an arrangement 390 Center of gravity 315a Central arrangement 410a Centrally symmetric polytope 114 Centrally symmetric polytope with few vertices 120 Centrally symmetric polytope, 2-neighborly 121b Centrally symmetric polytope, affine hull of f-vectors 169 Centrally symmetric polytope, Blaschke sums of parallelotopes 335 Centrally symmetric polytope, degree of total separability 218 Centrally symmetric polytope, Euler hyperplane 139 Centrally symmetric polytope, neighborly star-convex 121b Centrally symmetric polytope, number of faces 224b Centrally symmetric polytope, reducibility 322 Centrally symmetric polytope, simple or simplicial 198c Centrally symmetric polytopes, 3-dimensional, and refinements of the cube 205 Centrally symmetric polytopes, 4-dimensional, with 12 vertices 121b Centrally symmetric polytopes, d-dimensional, with 2d+2 vertices 121b Centrally symmetric polytopes, graphs of 3-dimensional 245 Centrally symmetric polytopes, neighborly families of 129 Centrally symmetric polytopes, valences of vertices of 3-dimensional 269 Centrally symmetric, (d-1)-neighborly simplicial spheres 121b Centrally symmetric, 2-neighborly simplicial spheres 121b Centrally symmetric, neighborly fans 121b Centrally symmetric, polytope see “Centrally symmetric polytope” Centroid 297 315a Centroid, curvature 307 Characteristic cone 24 Chromatic number of 423b Circle packing theorem 296a Circuit 200 Circuit code 381 389b Circuit, Hamiltonian see “Hamiltonian circuit” Circuit, simple 356 381 circumcircle 286 Circumradius 423c Circumscribable type 285 Circumsphere 284 Class of convex polytopes 325 Closed convex hull 14 Closed set 5 Closure of a set 6 Code 357 Code of spread s 382 Code, circuit 381 Code, discrete 382 Code, Gray 382 Code, path 382 Code, snake-in-the-box 382 Code, unit distance 382 Coding size of rational 4-polytopes 296d Coding size of rational polytopes 52a Coding size of the volume 340b Coface of a point set 88 Cohen — Macaulay property 198a Combinatorial automorphism, 3-connected planar graphs 252 Combinatorial automorphism, number of simple 3-polytopes 289 Combinatorial automorphism, regular polytopes 413 Combinatorial automorphism, symmetries of polytopes with few vertices 120 Combinatorial complexity of arrangements 410b Combinatorial equivalence of complexes 199 Combinatorial equivalence of diagrams 219 Combinatorial equivalence of polytopes 38 Combinatorial equivalence, isomorphism of Gale-transforms 89 Combinatorial equivalence, k-equivalence of polytopes 225 Combinatorial isomorphism see “Combinatorial equivalence” Combinatorial optimization, 0/1-polytopes 69a Combinatorial optimization, Hirsch conjecture 355b Combinatorial optimization, Menger’s theorem 224b Combinatorial type 38 90 Combinatorially equivalent 38 (see also “Combinatorial equivalence”) Combinatorially regular polytopes 413 Commutative algebra 198c Compact set 6 Complete metric space 6 COMPLEX 39 199 Complex hyperplane arrangement 410b Complex of an arrangement 390 Complex, abstract 206 Complex, boundary see “Boundary complex” Complex, cell 51 Complex, linked 40 Complex, polyhedral 51 Complex, simple 206 Complex, simplicial 59 67 Complex, topological 39 Complexity of a 4-polytope 198d Complexs, computing the number of 95 Complexs, sequences of 84 Computational convexity 52a Computational geometry 142a 410b Concentration of measure 30b Cone 23 Cone, associated 49 Cone, characteristic 24 Cone, generated by a set 9 Cone, pointed 24 Cone, polyhedral 36 Cone, spanned by a set 24 Configuration 93 391 Congruent polytopes 129b Congruent-faced polytope 414 Connected graph 212 Connected graph, k-connected graph 212 Connected sum 96b Containment problem 423c Content, k-content 416 Convergence 5 Convex body see “Convex set” Convex body, extremal structure 30a Convex combination 14 Convex function 13 37 Convex hull 14 Convex hull algorithm, asymptotically optimal 52a Convex hull algorithm, beneath and beyond 96b Convex hull algorithm, reverse search 52 a Convex hull problem 52a Convex hull program 52b Convex polyhedron 51 Convex polytope 51 (see also “Polytope”) Convex set 8 (see also “Convex body”) Convex set, algorithmic model 30b Convex set, general 30a Convex set, k-convex set 126 Convex set, protectively 29 Convex set, reducible 26 Convex set, spherically 10 30 Convex subdivision 199 Convexity, computational 52a Convexity, generalized 30b Convexity, hyperbolic 30b Covering number 423c Coxeter group 423a Crosspolytope see “Octahedron” cube 56 Cube, codes 381 Cube, largest simplex in a 423d Cube, polytopes without triangles 198d Cube, sections 72 Cubical polytope 59 Cubical polytope with at most 69b
Реклама
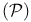-realizable complex 
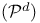-realizable”
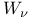path 
-transformation 
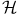-description 
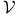-description 
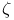-vect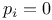or 
for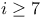 
vertices 
|
|
О проекте