Авторизация
Поиск по указателям
Grünbaum B. — Convex Polytopes
Обсудите книгу на научном форуме Нашли опечатку?
Название: Convex PolytopesАвтор: Grünbaum B. Аннотация: The appearance of Gruenbaum's book Convex Polytopes in 1967 was a moment of grace to geometers and combinatorialists. The special spirit of the book is very much alive even in those chapters where the book's immense influence made them quickly obsolete. Some other chapters promise beautiful unexplored land for future research. The appearance of the new edition is going to be another moment of grace. Kaibel, Klee and Ziegler were able to update the convex polytope saga in a clear, accurate, lively, and inspired way. —Gil Kalai, The Hebrew University of Jerusalem The original book of Gruenbaum has provided the central reference for work in this active area of mathematics for the past 35 years...I first consulted this book as a graduate student in 1967; yet, even today, I am surprised again and again by what I find there. It is an amazingly complete reference for work on this subject up to that time and continues to be a major influence on research to this day. —Louis J. Billera, Cornell University The original edition of Convex Polytopes inspired a whole generation of grateful workers in polytope theory. Without it, it is doubtful whether many of the subsequent advances in the subject would have been made. The many seeds it sowed have since grown into healthy trees, with vigorous branches and luxuriant foliage. It is good to see it in print once again. —Peter McMullen, University College LondonThe combinatorial study of convex polytopes is today an extremely active and healthy area of mathematical research, and the number and depth of its relationships to other parts of mathematics have grown astonishingly since Convex Polytopes was first published in 1966. The new edition contains the full text of the original and the addition of notes at the end of each chapter. The notes are intended to bridge the thirty five years of intensive research on polytopes that were to a large extent initiated, guided, motivated and fuelled by the first edition of Convex Polytopes. The new material provides a direct guide to more than 400 papers and books that have appeared since 1967. Branko Grünbaum is Professor of Mathematics at the University of Washington.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 2003Количество страниц: 466Добавлена в каталог: 30.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Polytope, shellability 142a Polytope, simple see “Simple polytope” Polytope, simplicial see “Simplicial polytope” Polytope, spherical 7a Polytope, stacked 198b Polytope, summand 316 Polytope, type (2,2) 69a 82 96b Polytope, type (2,d-2) 171b 428b Polytope, type (3,d-3) 171b Polytope, type (4,4) 69a Polytope, type (k,h) 58 65 69a 169 Polytope, type (r+2,s+t-1) 171b Polytope, unavoidable small faces 224b Polytope, uniform 171b 413 423a Polytopes, enumeration of see “Enumeration” Polytopes, number of see “Number” Polytopes, related 50 Poonem 20 Poonem, not being a face 30a Poonem, polyhedral sets 26 Positively homogeneous function 13 Primitive fixing system 423 Primitive illuminating set 422 Primitive polytope 423 Prism, d-prism 56 Prism, k-fold d-prism 56 Prismoid 57 Prismoid, generalized 65 Prismoid, indecomposability 323 Prismoid, proof of Euler’s theorem 131 Projection constant 73 Projection of a polytope 71 Projection, radial 23 Projective equivalence 5 Projective equivalence, Gale-transforms 89 Projective geometry 7b Projective space 4 Projective space, arrangements 390 Projective space, configurations 93 Projective space, Euler characteristic 142 Projective transformation 4 7b Projective transformation of convex sets 21 35 Projective transformation of d+3 points in 126 Projective transformation of polytopes 67 Projective transformation, admissible 7a Projective transformation, Gale-diagrams 87 Projective transformation, permissible 4 Projective transformation, piecewise 41 Projective transformation, polytopes inscribed into spheres 285 Projectively convex set 29 Projectively realizable sequence 405 Projectively regular polytope 412 Projectively unique 68 Projectively unique, d-polytopes with d+3 vertices 120 Projectively unique, non-rational 8-polytope 96 Projectively unique, polytopes with not, facets 208 Pseudo-hyperplane arrangement 410a Pseudo-hyperplane arrangement, number of simplicial regions 410b Pseudo-line 408 Pseudo-line arrangement 410a Pseudo-line arrangement, number of triangles 410b Pulling 82 96b Pushing 82 96b Pyramid 54 Pyramid, r-fold 54 Pyramidal polytope 68 88 Pyramidoid 63 Pyramidoid, indecomposability 323 Pyramids, f-vectors of r-fold 140 Pyramids, indecomposability of r-fold 323 Pyramids, r-fold, and d-polytopes with d+2 vertices 100 Pyramids, r-fold, and pyramidoids 64 Quasi-polyhedral 36 Quasi-simplicial polytope 59 Quasi-simplicial polytope, Euler hyperplane 137 Quasi-simplicial polytope, f-vectors 153 Radial projection 23 200 Radius of a polytope 341 Radon’s theorem 16 Radon’s theorem, k-neighborly polytopes 123 Ramsey theory 7b 30b Ramsey’s theorem 22 126 Random walk 340b Random-edge pivot rule 389b Random-facet pivot rule 389b Rational polytope 52a 92 Rational polytope, decidability of face lattices 96b Rational polytope, perturbing a polytope with d+3 vertices 119 Rational polytope, Steinitz’ theorem 244 Rational space, polytopes 92 Rational space, sections 76 Ray shooting 52a readability see “d-realizability” Readability of 2-complexes 253 Readability, see “ Readability, see “ Readability, 3-readability, of a sequence see “3-realizable sequence” Readability, projective, of a sequence see “Projectively realizable sequence” Reconstruction of duals of capped cubical polytopes from their 1-skeleta 234b Reconstruction of duals of cubical zonotopes from their 1-skeleta 234b Reconstruction of polytopes from their (d-2)-skeleta 234a Reconstruction of simple polytopes from their 1-skeleta 234a Reconstruction of simplicial polytopes from their [d/2]-skeleta 234a Reconstruction of zonotopes from their 1-skeleta 234b Reducible convex set 26 322 Reducible polytope 322 Reduction, proof of Steinitz’s theorem 237 (see also “ Reduction, proof on realizable sequences 272 Refinement map 199 Refinement of a complete graph in a polytopal graph 214 Refinement of a complex 199 Refinement of the boundary complex of a simplex 219 Reflection group see “Finite reflection group” Regular cell complex, Eulerian lattices 142b Regular cell complex, intersection property 142b Regular cell complex, strongly 142b Regular polytope 423a Regular polytope, affinely 412 Regular polytope, combinatorially 413 Regular polytope, projectively 412 Regular-faced polytope 414 Related polytopes 50 52c Relative boundary 9 Relative interior 9 428a Representation of a polytope 52a Representation of a polytope as a section 96a Representation of a polytope, 52a Representation of a polytope, 52a Representation of a polytope, alternative 52b Representation of a polytope, coding size 52a 296d Representation of a polytope, computation 52a Representation of a polytope, oracle 52b Representation of a polytope, polynomial inequalities 52b Reverse search 52a Rigidity theorem 411 Rigidity theory, lower bound theorem 198a Rigidity theory, Steinitz’s theorem 296a Rotation distances of trees 30b Rubber band method 296a Scalar product 2 Scheme of a polytope 90 Scheme, abstract 91 Schlegel diagram 43 52c Schlegel diagram, 3-polytopes 235 244 Schlegel diagram, circumcircles 287 Schlegel diagram, embedding graphs into cyclic 4-polytopes 212 Schlegel diagram, history 127 Schlegel diagrams, 3-diagrams not being 219 Section of a polytope 71 Selection theorem 10 325 Self-dual polytope 48 Self-dual polytope, pyramids 69 Self-dual polytopes, density of the family of 3-dimensional 82 Self-dual polytopes, enumeration of 3-dimensional 289 Semi-algebraic set 52b Semi-algebraic variety 96a Semiregular polytope 423a Semispaces 13 Separated set 10 Separated sets, strictly 10 Separation in graphs 217 Sewing 129a Shadow vertex pivot rule 389b Shape matching 315b Shellability of polytopes 142a Shellability, upper bound theorem 198a Simple circuit 356 381 Simple complex 206 Simple d-arrangement 391 Simple path 356 Simple polytope 58 Simple polytope, affine hull of f-vectors 170 Simple polytope, decomposability 321 Simple polytope, degree of total separability 218 Simple polytope, h-simple polytope 58 Simple polytope, incidence equation 144 Simple polytope, Perles’ conjecture on the facet subgraphs 234a Simple polytope, reconstruction from 1-skeleton 234a Simple polytope, refinements of boundary complexes 206 Simple polytope, relations between the Steiner points of the faces 311 simplex 53 Simplex 376 Simplex 379 Simplex algorithm 377 389b Simplex height 376 Simplex, combinatorial type 53 Simplex, embedding skeleta of simplices 210 Simplex, generalized bipyramid of two simplices 64 Simplex, sections of simplices 71 Simplex, simplices as regular polytopes 412 Simplex, spherical 306 Simplicial complex 59 Simplicial complex, embedding 67 202 224a Simplicial complex, minimal face numbers 179 Simplicial polyhedral complex 51 Simplicial polytope 57 Simplicial polytope with d+2 vertices 97 Simplicial polytope, angle-sums relations 307 Simplicial polytope, Dehn — Sommerville equations 171a Simplicial polytope, f-vector and h-vector 171a Simplicial polytope, f-vectors 145 Simplicial polytope, g-theorem 171b Simplicial polytope, Gale-transforms 88 Simplicial polytope, h-vector and face ring 171a Simplicial polytope, k-simplicial polytope 58 Simplicial polytope, neighborly polytopes 124 Simplicial polytope, reconstruction from [d/2]-skeleton 234a Simplicial polytope, stability 69 Simplicial polytope, upper bound problem 172 Simplicial polytopes, density of the family of 81 Simplicial polytopes, number of see “Number” Simplicial sphere, centrally symmetric see “Centrally symmetric” Simplicial sphere, g-theorem 198b Simplicial sphere, polytopality 121a Simplicial sphere, upper bound theorem 171a 198a Simplicial spheres, number of see “Number” Singular of degree s 269 Skeleton 138 Skeleton of a simplex 201 210 Skeleton, k-skeleton 138 Slack variable 96a Snake-in-the-box code 382 Space-filling 411 Spanning tree 296 Sphere 5 Sphere, shellable 96b Sphere, simplicial see “Simplicial sphere” Spheres, convexity on 10 30 Spherical arrangement 409 Spherical polytope, arrangements 392 Spherical polytope, Euler’s equation 142 Spherical polytope, incidence equations 145 Spherical simplex 306 Spherical space 7a Spherically convex set 10 30 SPREAD 382 Stable equivalence 96a Stacked polytope 198b Standard Gale-diagram 109 Stanley — Reisner ring 198a 198c Star 40 Star, k-star 138 301 Star-diagram 103 Star-diagram, simplicial polytopes 114 Steep 376 Steep height 376 Steepest edge pivot rule 389b Steiner point 308 315a Steiner point, history 313 Steiner point, translation classes 317 Steiner point, valuation property 315 Steinitz’s theorem on 3-polytopes 235 296a—296b Steinitz’s theorem on 3-polytopes, analogue for 2-arrangements 409 Steinitz’s theorem on 3-polytopes, enumeration of 3-polytopes 92 290 Steinitz’s theorem on 3-polytopes, modifications 244 Steinitz’s theorem on 3-polytopes, projective uniqueness 68 Steinitz’s theorem on convex hulls 17 Straszewicz’ theorem 19 Stretchable arrangement 408 Strict 375 Strict height 376 Strictly antipodal subset of 128 129b Strong d-ambiguity 225 228 Strong monotone Hirsch conjecture 355b Strongly isomorphic polytopes 52c Strongly regular cell complex see “Regular cell complex” Subdivisions of complete graphs 224b subspace 3 Subspace arrangements 410b Summand of a polytope 316 Supporting function 13 326 Supporting hyperplane 10 13 Sweep 142a Sylvester — Gallai theorem 410b Sylvester’s problem 404 (see also “Sylvester — Gallai theorem”) Symmetry of a polytope 120 Symmetry of a polytope, central see “Centrally symmetric polytope” Symmetry of a polytope, regular polytopes 412 Tarski’s procedure 96b Tarski’s theorem 91 Threshold gate 121b Tile type 423a Tiling of 423a Topological complex, Euler characteristic 142 Topological complex, incidence equation 145 Topological complex, polyhedral, convex, geometric complex 39 Toric g-vector 198c Toric h-vector 171b Toric variety 52c Toric variety and h-vector 171b Toric variety and the g-theorem 171b Toric variety, cohomology 198c Toric variety, Morse function 142a Torus 207 253 Totally positive matrix 129b Totally separated 217 Totally separated, degree of total separability 217 Tower 37 Towers of Hanoi 383 Transformation, adjoint 50
Реклама
 |
|
О проекте
|
|
О проекте



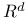
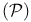 -readability, of a complex
-readability, of a complex 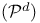 -realizable”
-realizable” -transformation”)
-transformation”)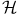 -description
-description  -description
-description  -path
-path