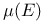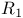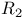Авторизация
Поиск по указателям
Boas R.P. — A Primer of Real Functions
Обсудите книгу на научном форуме Нашли опечатку?
Название: A Primer of Real FunctionsАвтор: Boas R.P. Аннотация: This is a revised, updated and significantly augmented edition of a classic Carus Monograph (a bestseller for over 25 years) on the theory of functions of a real variable. Earlier editions of this classic covered sets, metric spaces, continuous functions, and differentiable functions. The greatly expanded fourth edition adds sections on measurable sets and functions, the Lebesgue and Stieltjes integrals, and applications.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Fourth EditionГод издания: 1996Количество страниц: 314Добавлена в каталог: 11.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
110 112 23 24 43 110 see 14 120 183 240 264 140 107 139 91 24 221—224 25 109 217 24 43 44 197 23 45 49 51 57 32 35 172—173 73 199 43 15 228 240 172 14 20 237 Abel, Niels Henrik 121 123 Abel, Niels Henrik, convergence test 233 Absolute continuity 204—205 Absolute continuity, of an integral 210 212 216 Absolute convergence 209 Accuracy, numerical 237 242—244 Aczel, Janos 186 Aggregate 2 Agnew, Ralph Palmer 139 Airline space 23 Algebra, fundamental theorem of 59 Algebraic numbers 11—15 Algorithms 21 Almost everywhere 74 Almost everywhere, continuous 206 274 Almost everywhere, convergence 220 221 Almost everywhere, differentiability 155 165—170 204 214 215 Almost everywhere, finite 210 Almost everywhere, limit of continuous functions 202 Almost everywhere, zero derivative 160—164 204 205 Almost uniform convergence 202 Alphabet 3 Alsina, James 122 Alternating Series Test 233 Ampere, Andre Marie 103 Analytic function 47 69 189—192 Antecedent 19 Antiderivative 66 195 206 242 Antipodal points 100—102 antisymmetric 238 279 Apostol, Tom M. 228 Approximation by nonmonotonic functions 70 Approximation by open and closed sets 197—198 Approximation by polygonal functions 128 Approximation by polynomials 128—132 Approximation by rational numbers 75 Approximation by step functions 128 Approximation of a numerical series 237—243 Approximation of an integral 229—230 Approximation of continuous functions 126—132 Approximation of power series by partial sums 47 Arbitrary functions 84—85 87 154—155 Arbitrary shape 101 Arithmetic 7 242 246 Arithmetic mean 181—183 Austin, Donald G. 175 automobile 202 Average 136 181 215 220 Axiom of Choice xi 200 Aziz, Abdul Kadir 156 B 25 44 47 127 Baire category see “Category” Baire class 125 201—202 Baire measure 236 Baire, Rene 125 126 Baire’s theorem 61—72 123—126 192 Baker, Richard L. xii Balaguer, Ferran Sunyer i 72 Bamon, Rodrigo 138 Banach — Tarski paradox 200 Banach, Stefan 72 200 Bartle, Robert G. 205 Base 2 expansion 40—42 115—116 152 161—163 Base 3 expansion see “Base 2 expansion” Basis, Hamel 138 Beckenbach, Edwin F. 186 Beekmann, Wolfgang 61 Beesley, E. Maurice xii 158 Bellman, Richard 186 Benavides, Tomas Dominguez 75 Bernoulli numbers 241—242 Bernoulli polynomials 241 Bernstein equivalence theorem see “Schroeder — Bernstein theorem” Bernstein, Felix 21 Bernstein, Sergei 191 Bernstein’s theorem on analytic functions 191—192 Besicovitch, Abram Samoilovitch 73 Bessel’s inequality 222 Bibliography of bibliographies 4 Bicompactness 48 Big game hunting 52 Billions 14 237 Binary expansion see “Base 2 expansion” Binomial theorem 191 264 biology 44 Bird trap 46 Bisecting areas and volumes 101—102 Bisection method 46—47 Block of digits 244 Blumberg, H. 90 Boas, Anne Louise vii Boas, Harold Philip vii xii Boas, Mary Elizabeth Layne xi Boas, Ralph Layne vii Boas, Ralph Philip vii 157 192 193 243 244 Boghossian, Artin B. 72 Bolzano — Weierstrass theorem 45—48 50 59 60 91 Bonnet’s theorem 231 Borel, Emile 193 Borel, Emile, measure 236 Borel, Emile, sets 198 272 Borsuk’s theorem 100 101 Borwein, Jonathan M. and Peter B. 21 Bose Majumder, N.C. 138 Botsko, Michael W. 158 210 Bottazzini, Umberto 111 Bound, of derivates 150—151 Bound, positive lower 89 Boundary 27 Boundary, empty 28 Boundary, is closed 30 Boundary, nonempty 35 Boundary, of boundary 28 Boundary, of complement 28 Boundary, of neighborhood 28 Boundary, point 27 Bounded, above 5 Bounded, convergence 111 Bounded, convergence theorem 213 Bounded, derivative 70 Bounded, functional 234 Bounded, functions 25 110—112 209 Bounded, functions, continuous 45 46 48 89 Bounded, functions, not separable 44 Bounded, partial sums 233 Bounded, sequences 24 43 44 Bounded, set 7 26 Bounded, variation 203—204 216 226 228 230 234 Bourbaki, Nicolas 2 Box of maximum volume 182 Brennan, J.G. 104 Briggs, James M. 200 Bromwich, Thomas John l’Anson 123 Brown, Johnny M. 138 Brownian motion 72 Bruckner, Andrew M. xii 90 155 158 Buck, Ellen F. and Robert Creighton xi Bunyakovsky, Victor Ya. 185 Burckel, Robert B. viii 156 186 C 24 see C(E) 3 Calculation of 21 Calculator 242 Cantor function 161—163 204 216 Cantor function, characterization of 174 Cantor function, integral of 208 Cantor set 39—42 44 Cantor set, arithmetical description 41 Cantor set, distance property 134 Cantor set, first category 64 Cantor set, generalized 74—75 206 Cantor set, irrational points of 42 Cantor set, limit points of 39 40 44 Cantor set, measure zero 74 196 Cantor set, nowhere dense 40 Cantor set, uncountable 41 65 Cantor teepee 42 Cantor’s nested set theorem 62—63 Caratheodory’s criterion 198 200 Cardinality 8—20 Cargo, Gerald T. xii 157 Carroll, Francis W. 126 Cartan, Henri 193 Cartesian product 79 Catching a lion 46 Category 63—65 Category, for differentiate functions 70—72 193 Category, of level sets 152—153 Category, of points of discontinuity 125—126 Cater, Frank S. 76 174 193 Cauchy sequence 55—58 62 108 110 222 223 Cauchy, Augustin-Louis 108 Cauchy, Augustin-Louis, error of 108 121 Cauchy’s inequality 185 186 Center of gravity 180 193 Cetkovic, S. 157 Chain of elements 18—19 Chain rule 141 Chalice, Donald R. 174 Change of variable 261 268 Characterization of bounded set 7 Characterization of Cantor function 174 Characterization of continuous functions 92 Characterization of linear functional 236 Characterization of polynomials 67—69 Checkerboard 135 Chinn, William G. 104 Chittenden, Edward W. 103 chords 96—100 144 175—180 Chudnovsky, David V. and Gregory V. 21 Civin, Paul 103 Clark, H.M. xi class 2 Class, Baire 125 201—202 Clavius 200 clock 100 Closed interval 6 24 28 72 Closed sets 25—37 Closed sets, alternative definitions 29 Closed sets, approximation by 196—198 Closed sets, compact 49 Closed sets, complements of 29 Closed sets, contain limit points 29 Closed sets, intersections of 36—37 Closed sets, level sets 30 Closed sets, measure of 196 Closed sets, nowhere dense 38 Closed sets, of measure zero 174 Closed sets, unions of 36—37 Closure 35—36 Closure, diameter of 61 Closure, of neighborhood 37 Cluster point 29 Cobb, John 44 Coffee 102 Cohen, Paul J. xi Collection 1 2 Common error 151 Compact set 48—52 Compact set, closed subset of 49 Compact set, continuous function on 48—49 57 91—93 100 109 112 126—132 Compact set, distance attained for 60—61 Compact set, largest element 59 Competent analyst 186 Complement 3 Complement, boundary of 28 complete 56—58 64 112 222—224 Completion 56 Computation 21 237—243 Computer 20 21 195 203 237 243 Concave 180 181 184 Condensation of singularities 114 Confusion 86 91 108 208 229 Conjecture 160 Connected set 32—35 Connected set, 35 117 Connected set, 35 Connected set, continuous function on 92 Connectedness: intrinsic property 34 Consonant 3 Constant function 78 Constant, Euler’s 240 Contain 1 2 continuous curve 114—117 Continuous functions 24—25 83—89 Continuous functions, absolutely 204—205 216 Continuous functions, almost everywhere 206 274 Continuous functions, approximation of 126—132 Continuous functions, at most two-to-one 95—96 Continuous functions, bounded 45 89 Continuous functions, completeness of 112 Continuous functions, convex 175 177 Continuous functions, definitions 85—88 Continuous functions, determined by moments 131—132 Continuous functions, differentiable 140 151 Continuous functions, equivalence of definitions 88—89 Continuous functions, everywhere oscillating 69—70 Continuous functions, fixed points 100 Continuous functions, graphs 85 Continuous functions, intermediate value property 84 92 Continuous functions, limits of 202 Continuous functions, linear 133—134 Continuous functions, linear functionals on 233—236 Continuous functions, maxima 45—46 48—49 92 142 Continuous functions, measurable 201 Continuous functions, neighborhood in space of 26 Continuous functions, nondifferentiable 70—72 153 Continuous functions, of bounded variation 204 Continuous functions, on compact sets 127 Continuous functions, periodic 97—98 Continuous functions, pointwise convergence 109 Continuous functions, pointwise limits 123—126 Continuous functions, positive lower bound 89 Continuous functions, properties of 90—102
Реклама
 |
|
О проекте
|
|
О проекте



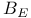

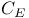
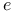
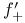 ,
, 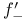
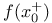 ,
, 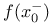
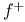 ,
, 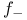 ,
, 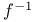
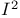
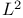
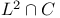

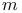
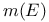
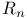
 -function
-function