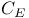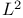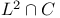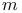Авторизация
Поиск по указателям
Boas R.P. — A Primer of Real Functions
Обсудите книгу на научном форуме Нашли опечатку?
Название: A Primer of Real FunctionsАвтор: Boas R.P. Аннотация: This is a revised, updated and significantly augmented edition of a classic Carus Monograph (a bestseller for over 25 years) on the theory of functions of a real variable. Earlier editions of this classic covered sets, metric spaces, continuous functions, and differentiable functions. The greatly expanded fourth edition adds sections on measurable sets and functions, the Lebesgue and Stieltjes integrals, and applications.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Fourth EditionГод издания: 1996Количество страниц: 314Добавлена в каталог: 11.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Oehring, Charles C. xii Olmsted, John Meigs Hubbell xii 72 One-sided derivative 140 177 178 One-to-one correspondence 8 One-to-one correspondence, Cantor set and real numbers 42 One-to-one correspondence, continuous functions and sequences 132 One-to-one correspondence, infinite set and proper subset 15 One-to-one correspondence, integers and even integers 9 One-to-one correspondence, interval and line 16 One-to-one correspondence, interval and square 17 117 One-to-one correspondence, sequences and numbers 20 One-to-one correspondence, sets of integers and real numbers 19 20 One-to-one function 91 Open and closed set 28 29 32 Open intervals 28 Open sets 25—37 Open sets, alternative definitions 29 Open sets, complement closed 29 Open sets, disjoint from boundary 29 Open sets, images and inverse images of 88 Open sets, measure of 196 Open sets, neighborhoods 28 Open sets, structure in 30 Open sets, union and intersection 37 Openness: not intrinsic property 33 Operator 79 Ordered pair 22 77—80 91 Ordinates of maxima 142 156 Oresme, Nicole 256 Orthogonal functions 221—224 Orthonormal 221 Oscillating curve 32 Oscillating function 69—70 203 Osgood, William Fogg 126 268 Ostrowski, Alexander M. 186 Outer measure 172 197 198 Oxtoby, John C xii 75 103 104 Paige, Lowell J. 157 Pambuccian, Victor 90 Pancake 101—102 Paradox 4 16 200 227 Parametric equations 115 116 Parks, Harold R. 193 Partial summation 232 Partial sums 47 52 54 233 237—243 Partition 206—208 236 Pea 200 Peano curve 114 Pecaric, Josip E. 186 Pencil 85 242 Perfect set 37 Perfect set, continuous functions on 125 Perfect set, nowhere dense 38 Periodic functions 97—98 115 143 238 240 242 Petard, H.W.O. 52 Petersen, Bent E. 229 Pfaff, Donald C 158 Picnic table 104 Piecewise monotonic 158 177 Piranian, George 174 Plancherel, Michel 139 Plato 156 Plaza, Sergio 138 Point 1 Point, as nowhere dense set 38 65 Point, of density 172 Pointwise convergence 108—109 123—126 Polya, George 122 138 139 156 186 Polygonal function 127 128 Polynomials 59 Polynomials, approximating continuous functions 43 128—132 Polynomials, Bernoulli 241 Polynomials, characterized by vanishing derivatives 67—69 Polynomials, extremal problems for 182 Polynomials, power series reducing to 47 Polynomials, with integral coefficients 11—12 20 Pompeiu, Dimitrie 156 Pondiczery, Ersatz Stanislaw 52 Porter, Gerald J. 158 Posey, Eldon E. 156 Positivity of metric 22 Poussin, Charles Jean de La Vallee 126 Power series 47 189—192 Preston, Richard 21 Priestley, William McGowen 75 prime factors 82 Primitives 195 probability 72 207 224 Product, cartesian 79 Product, of continuous functions 90—91 Product, of sets 3 Progression, geometric 52 Pronunciation 225 Proper, maximum 142 Proper, subset 2 15 Pure existence proof 14 Pure jump function 160 Quadrillionth 14 quantum mechanics 225 Quotients of continuous functions 90—91 RADIUS 25 Radius, of convergence 192 Rado, Tibor 175 Randolph, John F. 138 RANGE 77 Range, of continuous functions 92 93 Range, of derivatives 143—145 Rational numbers countable 11 Rational points, Bolzano—Weierstrass fails for 47 Rational points, boundary of 249 Rational points, dense 38 42 Rational points, disconnected 32 Rational points, incomplete 64 Rational points, neither open nor closed 29 Rational points, no interior 26 Real functions 3 79 Real numbers 5—8 Real numbers, not countable 15 Real numbers, number of sequences of 20 Real numbers, number of sets of 17 Real variable ix 79 Reciprocal 91 Redheffer, Raymond M. 193 Reich, Ludwig 138 Reich, Simeon 157 Reichbach, Marian 21 Remainder (Taylor’s theorem) 187 Repeated integrals 66 Restriction 78 Restriction, continuous, discontinuous 86—87 Riemann integration 206 209 222 Riemann zeta function 243 Riemann-Stieltjes integrals 224—228 Riesz representation theorem 233—236 Riesz — Fischer theorem 222 224 Riesz, Frigyes 158 166 174 175 205 222 224 234 Riesz’s lemma 166—168 170 Right-hand derivative 140 Rigid motions 200 Rising Sun Lemma 166 269 Roberts, John Henderson 103 Rolle’s Theorem 103 104 156 Rooij, Arnoud C.M. van 126 Rosenbaum, J.T. 104 Rosenthal, Arthur 193 Ross, Kenneth A. 229 Rosser, J. Barkley 83 Rota, Gian-Carlo 139 Royden, Halsey L. 205 Rubel, Lee A. 174 175 Rudin, Walter 76 217 Rule 79 Rule, chain 141 Rule, divide and 264 Rule, of arithmetic 246 Ruler function 85 154 158 218 Sack, John 52 Sahara desert 46 Saks, Stanislaw 73 155 156 174 Salzmann, Helmut R. 193 Samelson, Hans 156 Sandwich theorem 102 Saw—tooth function 70 Scalar, field 79 Scalar, product 221 Schaffter, Thomas 200 Schiff, Leonard I. 225 228 Schikhof, Wilhelmus Hendricus 126 Schoenberg, Isaac Jacob 122 Schroeder — Bernstein theorem 18—20 Schwartz, Laurent 229 Schwarz, Hermann Amandus 186 229 Schwarz’s inequality 185 221 223 229 Second category 64 258 Second category, complete metric space is 64 Second category, function continuous and not differentiable at points of set of 153 Second category, nowhere differentiable functions are set of 71 Second category, set of, with measure zero 74 75 Second derivative 179 Seebach, J. Arthur, Jr. 44 Segal, Arthur C. xii 158 Separable 42—44 SEQUENCE 78—81 Sequence spaces 23—24 Sequence, bounded 24 43 44 59 Sequence, boundedly convergent 111 Sequence, Cauchy 55—58 Sequence, convergence of 52—56 Sequence, differentiation of 119 145—147 Sequence, finite 53 80 Sequence, increasing 57 Sequence, integration of 117—122 212—214 Sequence, monotone convergence 112 Sequence, of functions 108—111 201 Sequence, of moments 131 Sequence, of numbers 20 53 Sequence, of partial sums 54 Sequence, orthogonal 221 Sequence, orthonormal 221 Sequence, pointwise convergence 108 Sequence, uniform convergence 110—122 Sequence, upper and lower limits 104—107 Series 52—55 Series, connection with integrals 220—221 Series, convergence of 183 214 Series, differentiation of 164 171—173 Series, divergent, summed 55 Series, Fourier 225 231 Series, harmonic 196 237 242 244 256 Series, M-test 111 Series, numerical computation of 237—243 Series, of continuous functions 108 121 Series, of monotonic functions 171—172 Series, of orthogonal functions 221—224 Series, partial sums of 237—243 Series, power 47 224 Series, special, summed 120—122 237 Series, Stieltjes integrals applied to 232—233 Series, Taylor 189—192 Series, trigonometric 207 225 231 Set of all sets 4 16 Sets 1—4 Sets, arbitrary, as metric spaces 25 Sets, Borel 198 Sets, boundary of 27 Sets, bounded 7 26 45 49 Sets, Cantor 39—42 74—75 Sets, category of 64 Sets, closed 28 Sets, compact 48 Sets, connected 32 Sets, countable 9 Sets, dense 38—44 Sets, density of 172—173 Sets, disjoint 3 Sets, empty 2 Sets, finite 9 Sets, first category and positive measure 74 Sets, infinite 9 15 Sets, interior of 26 Sets, intersection of 3 Sets, measurable 197 198 Sets, nested 61—62 Sets, nonmeasurable 198—200 Sets, nowhere dense 38—44 Sets, nowhere dense perfect 39 Sets, null 209 Sets, of distances 133 Sets, of limit points 30 Sets, of measure zero 73—75 173 198 Sets, of positive integers 19 Sets, of positive measure 199 206 211 Sets, of real numbers 5—8 Sets, open 28 Sets, perfect 37 38 Sets, product of 3 Sets, second category and measure zero 74 Sets, uncountable 9 14—15 Sets, uncountable and measure zero 74 Sets, union of 3 Shanks, Daniel 20 Shkarin, S.A. 73 Shuchat, Alan Howard xii Sibling vii Sierpinski, Waclaw 83 90 155 200 Sierpinski’s theorem 73 Silverman, Stephen 138 Simoson, Andrew 200 Sine function 78 182 190 Singh, Avadhesh Narayan 157 Singular functions 161—164 174 Size of sets 73—75 slope ix 72 100 147 177 179 262 Snake 33 Solovay, Robert M. 200 Sophomore 44 Space 2 21 Space, complete 56 64 112 Space, metric 21—25 Space, separable 42 Space-filling curve 114 Spaces, special, 25 44 47 127 Spaces, special, 110 Spaces, special, 24 26 108 233 Spaces, special, 23 24 43 Spaces, special, 110 Spaces, special, 221—224 Spaces, special, 25 109 Spaces, special, 217 236 Spaces, special, 24 43 44 Spaces, special, 23 Spaces, special, integral points 26 38 Spaces, special, rational points 29 47 56 62 Square 17 33 115 116 134 182 Squire, William 244 Staircase 96 Steen, Lynn Arthur 44 Steenrod, Norman Earl 104 Steinhaus, Hugo 138 200 Step functions 127—128 214 226 276
Реклама
 |
|
О проекте
|
|
О проекте