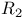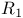Авторизация
Поиск по указателям
Boas R.P. — A Primer of Real Functions
Обсудите книгу на научном форуме Нашли опечатку?
Название: A Primer of Real FunctionsАвтор: Boas R.P. Аннотация: This is a revised, updated and significantly augmented edition of a classic Carus Monograph (a bestseller for over 25 years) on the theory of functions of a real variable. Earlier editions of this classic covered sets, metric spaces, continuous functions, and differentiable functions. The greatly expanded fourth edition adds sections on measurable sets and functions, the Lebesgue and Stieltjes integrals, and applications.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Fourth EditionГод издания: 1996Количество страниц: 314Добавлена в каталог: 11.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Geometric progression 52 Geometry 21 22 German mathematician 229 Gillespie, D.C 103 Goedel, Kurt xi Goffman, Casper 217 Goldberg, Richard R. 52 224 Goldowsky, G. 174 Gould, Henry W. 244 Graduate Record Examination 156 Graph 79 85 95 100 126 133 175 Gravity, center of 180 193 Greatest integer function 158 227 238 277 Greatest lower bound 6 7 Green, John W. 138 Gustin, William 138 Haber, S. xii Halmos, Paul R. 262 Ham sandwich theorem 102 Hamel basis 138 Hamel, Georg 138 139 Hardy, Godfrey Harold 61 83 138 186 207 243 Harmonic series 196 237 242 256 Harrold, Orville G. 103 Healthy skepticism x Heath, Thomas L. 200 Hegyvari, Norbert 244 Heine — Borel theorem 49—51 Heine — Borel theorem, converse of 51 Heine — Borel theorem, in R_{2} 50 Heirloom vii Heligoland bird trap 46 Hellmann, M.S. 21 Hersch, Joseph 139 Heuer, Gerald A. 158 Hewitt, Edwin 217 Hildebrandt, Theophil Henry 72 Historical reasons 241 Hobson, Ernest William 156 Holder’s Inequality 185 Home-made supercomputer 21 Hopf, Heinz 103 104 Horizontal chords 97—99 144 Hrbacek, Karel 138 Huggins, Frank N. 206 Hunting 52 Hurewicz, Witold 122 Hypotenuse 248 Idea, misleading 237 Identity function 81 Image 79 Image, inverse 88 Image, not necessarily open 88 Improper, integral 279 Improper, maxima 142 Increasing, at a point 141 155 Increasing, bounded sequence 57 Increasing, function 113 141 149 158 Indefinite integrals 117 119 195 214 216 Inequality, arithmetic and geometric means 181 Inequality, Bessel 222 Inequality, between sines and cosines 182 Inequality, Cauchy 185 Inequality, for integrals 181 Inequality, Holder 185 Inequality, Jensen 180—182 185 Inequality, midpoint 176 Inequality, Minkowski 24 184 Inequality, Schwarz 185 221 223 Inequality, triangle 22 Inf, infimum 6 7 Infinite, derivative 70—71 140 151 152 174 Infinite, measure 197 Infinite, numbers 7 Infinite, sequences 23—24 55—61 Infinite, series 52—55 189 237—243 Infinite, sets 8—20 45—47 Infinitely differentiate functions 118 120 186—192 Inner measure 198 Inner product 221 Instruction, undergraduate 225 Integer points of 10 26 Integers 8 19 Integrable functions 202 206 208—210 Integrable functions, Riemann 117 118 Integral test 220 239 Integrals 195—243 Integrals, connection with sums 220—221 Integrals, derivatives of 214—215 Integrals, inequalities for 181 Integrals, Lebesgue 206—224 Integrals, mean-value theorem for 229—230 Integrals, of derivatives 215—216 Integrals, of periodic functions 97 Integrals, repeated 66 Integrals, Riemann 206 Integrals, Stieltjes 224—236 Integrals, vanishing of 66 Integration by parts 187 227 228 231—233 239—241 275 Integration of sequences 117—122 212—214 intercept 102 262 Interior 26 Intermediate value property 84—85 Intermediate value property, for continuous functions 92 Intermediate value property, for derivatives 143 156 Intermediate value property, of 93—102 Intersection 3 Intersection, of closed sets 36—37 Intersection, of open sets 37 interval 6 Interval, closed, as a union of closed sets 72 Interval, collection is countable 30 Interval, open and closed 28 Intrinsic property 34 Inverse, function 91 Inverse, image 88 Inverse, tangent 164 Italian edition 155 Jech, Thomas 138 Jensen’s Inequality 180—182 185 Joggers 104 Johnson, Peter D., Jr. 72 Jump 85 151 159—161 Jump function 160 Kaplansky, Irving 61 Kestelman, Hyman 138 175 Klamkin, Murray S. 186 Kleiner, Israel 83 Knife 101 Konig, Heinz 186 Kraft, Roger L. 138 Krantz, Steven George 193 Kuczma, Marek 186 Kuratowski, Kazimierz 37 La Vallee Poussin, Charles Jean de 126 Landau, Edmund 132 Laplace transforms 224 Lattice points 10 Law of the mean see “Mean-value theorem” Least upper bound 5 Least upper bound, property 5—7 56 Lebesgue — Stieltjes integrals 224 Lebesgue, differentiation theorem 175 Lebesgue, Henri Leon 90 126 175 207 Lebesgue, integral 206—224 Lebesgue, measurable 197 201 Lebesgue, measure 195—200 Lee, Ken W. 138 Left-hand derivative 140 Lehmer, Derrick Henry 244 Lemma Riesz 166 Lemma, Fatou 213 Lemma, flowing water 166 Lemma, rising sun 166 Level sets 152 Levit, Robert J. 103 Levy, Paul 103 262 Librarian 4 Limit of derivative 151 187 Limit of function 107 Limit of integral 136—138 279 Limit of integration 227 Limit of monotonic function 159 Limit of sequence 54—56 58 Limit of sequence, boundedly convergent 111 Limit of sequence, increasing 57 Limit of sequence, nonuniformly convergent 112 114 Limit of sequence, of continuous functions 108 123—126 Limit of sequence, of derivatives 145—147 Limit of sequence, of differentiable functions 119 Limit of sequence, of monotonic functions 113 Limit of sequence, uniformly convergent 110—122 Limit of sums approximating an integral 226 Limit point 29—30 45—46 58—59 Limit, lower (lim inf) 104—107 Limit, upper (lim sup) 104—107 Line, supporting 179 Linear, functionals 233—236 Linear, functions 132—138 Lion 46 Liouville numbers 75 Lipiriski, Jan Stanislaw 174 Littlewood, John Edensor 138 186 Locus 23 173—174 log 2 121 Logarithm 80 Logical difficulties 4 Lorch, Edgar Raymond 126 Lorch, Lee 122 Lower, bound 6 Lower, limit 109 Lower, sums 208 M-test 111 115 159 163 264 Majumder, N.C. Bose 138 Mapping 79 Markus (Marcus), Solomon 157 Masses 224 Maxima 6 142 Maxima, computing by integration 217—219 Maxima, improper 142 Maxima, number of 142—143 Maxima, of compact set in 59 Maxima, of functions 46 93 142 Maxima, proper 142 May, Kenneth Ownsworth 138 McCarthy, John 72 McHugh, James A.M. 193 McLeod, Robert M. 211 Meager set 64 Mean-value theorem 143—145 229—230 Mean-value theorem, Bonnet 231 Mean-value theorem, generalized 148—149 152 Means, arithmetic and geometric 181—182 Measurable functions 201—205 Measurable sets 197 Measure, Baire 236 Measure, Borel 236 Measure, finite 210 Measure, inner 198 Measure, Lebesgue 195—200 Measure, of an interval 196 Measure, of points at given distance from a set 173—174 Measure, outer 172 197 198 Measure, positive 134 211 Measure, zero 73—75 160 165 209 Mechanics 224 Member 1 Memorial vii Memory, J.D. 104 Menger, Karl 83 Metcalf, Frederic T. 103 Metric 22 Metric, space 21—25 Middle thirds 39 134 Midpoint inequality 176 Miller, Anthony D. 157 Million 20 Minimum 6 Minkowski’s inequality 24 184 186 218 223 Minty, George J. 83 Mirkil, Hazleton 193 Misleading idea 237 Mitrinovic, Dragoslav S. 186 Model 79 Molecule 102 moment 131 224 Monotone convergence 112 214 Monotonic functions 94 158—174 Monotonic functions, bounded 159 226 Monotonic functions, bounded variation 203 Monotonic functions, convergence of 159 Monotonic functions, differentiability 155 161 165—170 Monotonic functions, integral test 220 Monotonic functions, jumps of 159—160 Monotonic functions, limits 159 Monotonic functions, measurable 201 Monotonic functions, sequence of 113 Monotonic functions, series of 171—172 Monotonic functions, singular 161 Monotonic functions, strictly 158 Morayne, Michal 156 Morgenstern, Dietrich 193 Morse, Anthony Perry 73 157 158 Motions, rigid 200 Mountain 104 166 Multiple-valued 77 Munroe, Marshall Evans 52 Neighborhood 25 37 Neighborhood, boundary of 28 Neighborhood, closure of 36 37 Neighborhood, diameter of 61 Neighborhood, in C 26 Neighborhood, in lattice 26 Neighborhood, is open 26 28 Nested sets 61—62 Ng, Che Tat 186 Nineteenth century 59 70 108 Niven, Ivan Morton 21 186 Noncollinear points 50 Nondecreasing function 113 149 150 158 171 174 177 213 230 Nondifferentiable functions 70—72 Nonincreasing function 158 Nonmeasurable set 198 200 Norm 218 221 Norton, Alec 158 Nowhere dense sets 38—44 63 66 67 69 71 Nowhere dense sets, closed 38 Nowhere dense sets, complement of dense open set 69 Nowhere dense sets, perfect 39 Nowhere dense sets, singletons 65 Nowhere differentiate 70—72 122 131 154 273 Null set 209 Number of subsets 16—17 Number theory 14 135 Numbers, algebraic 11—15 Numbers, rational 11 Numbers, real 5—8 Numbers, transcendental 12 14—15 75 Nurcombe, J.R. 186 Nymann, J.E. 158
Реклама
 |
|
О проекте
|
|
О проекте