|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bender C., Orszag S. Ч Advanced Mathematical Methods for Scientists and Engineers |
|
|
 |
| ѕредметный указатель |
Parametric amplifier 568p
Patching 335Ч336 497Ч504 500Ч505f 527
Period T of DuffingТs equation 548 567p
Period T of Rayleigh oscillator 477Ч479
Periodic behaviors for difference equations 238 246p
Periodic behaviors, asymptotic relations for 107Ч112 150Ч152 161Ч164
Periodic behaviors, Floquet theory 560Ч561 568p
Periodic behaviors, limit cycles see УLimit cyclesФ
Periodic behaviors, oscillators see УOscillatorsФ
Periodic behaviors, oscillatory integrals see УStationary phase method
Periodic behaviors, resonant and secular behavior 544Ч545
Periodic behaviors, slowly varying frequency 556 558Ч559
Perturbation problems, regular, initial-value problems 321Ч322 323f 327 329f
Perturbation problems, regular, roots of polynomials 319Ч320 328Ч330 330t 331f
Perturbation problems, regular, Schrodinger eigenvalue problem 330Ч335 354Ч355
Perturbation problems, singular, boundary-layer see УBoundary-layer problemsФ
Perturbation problems, singular, boundary-layer problems solved by asymptotic matching 337Ч341
Perturbation problems, singular, evaluation of integrals using asymptotic matching 341Ч349 365Ч366p 515Ч519
Perturbation problems, singular, initial-value problems solved by asymptotic matching 336Ч337
Perturbation problems, singular, multiple-scale see УMultiple-scale perturbation problemsФ
Perturbation problems, singular, roots of polynomials 325Ч326 361p
Perturbation problems, singular, Schrodinger eigenvalue problem 334Ч335 353 359Ч360
Perturbation problems, singular, WKB see УWKB problemsФ
Perturbation series 319Ч367
Perturbation series for eigenvalues and eigenfunctions 333Ч335 363p
Perturbation series in boundary-layer problems 428Ч429 431Ч435 440Ч455 477Ч479
Perturbation series in multiple-scale problems 545Ч551 561Ч566
Perturbation series in WKB problems 486Ч487 493Ч494 496 534Ч539
Perturbation series, derivation from asymptotic matching 337 342Ч349
Perturbation series, introductory discussion 317Ч318
Perturbation series, summation of 318 368Ч415 547Ч549
Perturbation series, Taylor series vs. 66 321Ч323 323f
Perturbation series, zeroth-order (leading) term in 320Ч321 324
Perturbation theory for linear eigenvalue problems 330Ч335
Perturbation theory, asymptotic matching 335Ч349
Perturbation theory, boundary-layer theory 326 419Ч484
Perturbation theory, dissipative and dispersive phenomena in 484Ч486
Perturbation theory, general procedures of 319Ч323
Perturbation theory, local and global breakdown in 484Ч485
Perturbation theory, mathematical structure of perturbative eigenvalue problems 350Ч361
Perturbation theory, multiple-scale 327Ч328 329f 540Ч568
Perturbation theory, philosophy of 317Ч318 368
Perturbation theory, regular, definition of 324
Perturbation theory, singular, definition of 324
Perturbation theory, unperturbed problem 321 324 333
Perturbation theory, WKB theory 326Ч327 328f 484Ч543
Phase space 171Ч197
Phase space, asymptotic matching in 337
Phase space, definition of 172
Phase space, higher-dimensional 185Ч197
Phase space, phase line 174Ч175
Phase space, phase plane 175Ч185 468Ч479 546Ч547
Phase space, phase sphere 202Ч203p 203f
Phase space, volume in 190Ч191 204p
Physical optics approximation as leading asymptotic behavior of WKB series 494Ч533
Physical optics approximation for GreenТs functions 497Ч504 500Ч505f
Physical optics approximation for higher-order equations 496Ч497
Physical optics approximation in complex plane 541p 542p
Physical optics approximation, accuracy of 494Ч497
Physical optics approximation, definition of 494Ч495
Physical optics approximation, derived using multiple-scale theory 556 558Ч559
Physical optics approximation, failure of 495Ч496
Physical optics approximation, failure of, at turning points 497 568p
Physical optics approximation, integrals of 490Ч491 500Ч504 513Ч519 540Ч541p
Physical optics approximation, normalization of 490 513Ч519
Physical optics approximation, validity of 494Ч497 506Ч508 521
Poincare plot 188 189f 190f
Polynomials, Bernoulli 305 315p
Polynomials, finding roots of 234Ч235 24lp 319Ч320 325Ч326 328Ч330 330t 331f 332f 352 354 361p 363p 366p
Polynomials, Hermite 55 99 133 244p
Polynomials, Laguerre 244p
Polynomials, Legendre 55p 229 231 232t 243p 309p
Potential 331 520Ч521 521f 526Ч527
Potential barriers,  -function 526Ч527 -function 526Ч527
Potential barriers, scattering off peak of 531Ч533
Potential barriers, tunneling through 524Ч531
Predatory-prey systems 179Ч183 180Ч182f
probability density 543p
Psi function  see УDigamma functionФ see УDigamma functionФ
Quantization condition, WKB see УEigenvalue conditionФ
Quantum anharmonic oscillator 334Ч335 337Ч338 353Ч354 353t 359Ч360 366Ч367p
Quantum harmonic oscillator 28 133 332Ч333 522Ч533 538
Quasiclassical approximation see УWKB theoryФ
Radioactive decay 543p
Ramp function 17
Random behaviors , Poincare plot 188 189f 190f
Random behaviors in phase space 188Ч189 190f 192Ч195 195Ч197f
Random behaviors of difference equations 237Ч239 239t
Rapid variation on global scale 326Ч327 328f 493
Rapid variation on local scale (at boundary layers) 326 327f 493
Rapid variation, definition of 484Ч485
Rayleigh oscillator, boundary-layer analysis of 468Ч479 476Ч478f 483p
Rayleigh oscillator, multiple-scale analysis of 554Ч556 556f 557f
Rayleigh oscillator, period of 477Ч479
Rayleigh ЧRitz variational procedure 352
Recessive see УSubdominanceФ
Recursion (recurrence) relations see УDifference equationsФ
Reduction of order for difference equations, homogeneous linear 43Ч45 56p
Reduction of order for difference equations, inhomogeneous linear 51Ч52 55p 56p
Reduction of order for difference equations, using generating functions 46
Reduction of order for differential equations, homogeneous linear 13 32p
Reduction of order for differential equations, inhomogeneous linear 19 32p 333
Reduction of order for differential equations, nonlinear 24Ч27 34p 35p 156
Reflection coefficient R 527 531 533
Regular perturbation theory see УPerturbation theoryФ
Regular singular points, of difference equations, definition of 207
Regular singular points, of difference equations, Frobenius series about 212Ч214
Regular singular points, of difference equations, leading asymptotic behavior near 207Ч210
Regular singular points, of differential equations, definition of 62 64
Regular singular points, of differential equations, Frobenius series near 68Ч76 452
Regular singular points, of differential equations, local behavior near 68Ч76 452Ч453
Regular singular points, of differential equations, Taylor series near 63
Regular singular points, of differential equations, Taylor series near, failure of 68Ч69
Resonant behavior 544Ч545 (see also УSecular behaviorФ)
Resonant scattering 542Ч543p
Riccati differential equation, conversion to second-order linear 21 151 156 483p
Riccati differential equation, definition of 20
Riccati differential equation, reduction to Bernoulli equation 21
Riccati differential equation, soluble and insoluble 4 22 27
Riccati differential equation, spontaneous singular points of 149Ч152 150f 152f 153t 197Ч198p
Richardson extrapolation 375Ч376 377t 378t 379 411Ч412p
Riemann integrals, approximating sums by 303Ч305
Riemann zeta function see УZeta functionФ
Riemann Ч Lebesgue lemma 277Ч278 285 311p
Roots of polynomials, finding, BernoulliТs method for 241p
Roots of polynomials, finding, Hermite polynomials 244p
Roots of polynomials, finding, Laguerre polynomials 244p
Roots of polynomials, finding, Legendre polynomials 231 232t
Roots of polynomials, finding, NewtonТs method for 234Ч235
Roots of polynomials, finding, perturbation theory for 319Ч320 325Ч326 328Ч330 330t 331f 332f 361p 363p
Roots of polynomials, finding, SylvesterТs eliminant for 352 354 366p
Saddle points, in autonomous systems, one-dimensional 174Ч175 174f
Saddle points, in autonomous systems, two-dimensional 177 179Ч182 180Ч182f
Saddle points, in method of steepest descents, approximation to integrals with 290Ч300
Saddle points, in method of steepest descents, definition of 288
Saddle points, in method of steepest descents, movable 295
Saddle points, in method of steepest descents, second-, third-, and fourth-order 289Ч290 290Ч292f
Scale-invariant equations 25Ч26 156
Scattering off peak of potential barrier 531Ч533 542p
Scattering problems 524Ч533 542Ч543p
Schrodinger equation, eigenvalue problem, analytic structure of eigenvalues as functions of perturbation parameter 351Ч361
Schrodinger equation, eigenvalue problem, eigenvalues for 27Ч29 330Ч335
Schrodinger equation, eigenvalue problem, perturbative solution of 330Ч335
Schrodinger equation, eigenvalue problem, WKB solution of 519Ч523 523t 524Ч52 542p 543p
Schrodinger equation, leading asymptotic behavior of nth-order 88 102Ч103 103f 496Ч497
Schrodinger equation, reduction of general second-order linear differential equation to 32p
Schrodinger equation, time-dependent 524Ч525 543p
Schrodinger equation, turning points of 497 521 521f
Schrodinger equation, WKB approximation for second-order 486Ч488 489 494Ч496 504Ч539
Sector of validity for asymptotic relations 113Ч118 114f 115f 130Ч136
| Secular behavior, definition of 545
Secular behavior, elimination of 550 553 555 558Ч559 564 566 566Ч567p
Secular behavior, summation of leading secularities 547Ч549
Semiclassical approximation see УWKB theoryФ
separable differential equations 3 23 24 30p
Shanks transformation, definition of 370
Shanks transformation, Euler Ч Maclaurin sum formula vs. 379
Shanks transformation, examples of 370Ч375 370t 371f 373t 374f
Shanks transformation, failure of 375 381
Shanks transformation, generalized (higher-order) 389Ч392 412p
Shanks transformation, iterated 370Ч374
Shanks transformation, roundoff error 372 410Ч411p
SimpsonТs rule 411Ч412p
Singular perturbation theory see УPerturbation theoryФ
Singular points of difference equations, definition and classification of 206Ч207
Singular points of difference equations, local analysis near 207Ч210 212Ч218 223Ч233
Singular points of differential equations, at  64 64
Singular points of differential equations, classification of 62Ч66
Singular points of differential equations, fixed 146 158
Singular points of differential equations, irregular 63Ч65 76Ч103
Singular points of differential equations, local behavior near 68Ч103
Singular points of differential equations, regular 62Ч63 68Ч76 452Ч453
Singular points of differential equations, removing 66
Singular points of differential equations, spontaneous (movable) 7 146Ч153 158 197Ч198p 554f
Slow variation 484Ч485
Snowplow problem 33p
Sommerfeld contour 293 293f 298
Spiral points 176Ч179 181Ч184 181f 182f 184f 192Ч194f 556f 557f
Spontaneous (movable) singular points for first Painleve transcendent 158
Spontaneous (movable) singular points for Riccati equations 149Ч152 150f 152f 153t 197Ч198p
Spontaneous (movable) singular points in complex plane 149
Spontaneous (movable) singular points, definition and discussion of 7 146Ч153
Spontaneous (movable) singular points, infinite number of 150Ч153
Spontaneous (movable) singular points, which are not poles 164Ч166
Stability of critical points, higher-dimensional 186 189 191
Stability of critical points, oneЧand two-dimensional 174Ч177
Stability of first Painleve transcendent 161 163Ч164
Stability, Floquet theory 560Ч561
Stabilityof solutions to Mathieu equation 561Ч566 568p
Stationary phase, method of 276Ч280 286 311Ч312p 347
Stationary points of order p 278Ч280
Stationary points, infinite-order 285Ч287
Steepest descents, method of 280Ч302
Steepest descents, method of, expanding Fourier integrals using 281Ч287 291 293Ч294
Steepest descents, method of, for complex parameter 300Ч302 313Ч315f7
Steepest descents, method of, for integrals with saddle points 290Ч300
Steepest descents, method of, steepest-descent and constant-phase paths in 282Ч287
Steepest descents, method of, use of, where LaplaceТs method fails 296Ч300
Steepest-ascent paths see УSteepest-descent pathsФ
Steepest-descent paths, definition and formal discussion of 282Ч283 282f 287Ч289
Steepest-descent paths, introduction to use of 282Ч287
Steepest-descent paths, rotation of in complex plane 301Ч302 301f 302f method
Step function 16 18
Stieltjes function (Stieltjes integral), asymptotic expansion of 260
Stieltjes function (Stieltjes integral), continued-fraction representation of 396 406Ч407
Stieltjes function (Stieltjes integral), definition and properties of 120Ч122 406
Stieltjes function (Stieltjes integral), moment integrals 121Ч122 405
Stieltjes function (Stieltjes integral), sum of Stieltjes series 120Ч122
Stieltjes function (Stieltjes integral), weight (density) function 121Ч122 405Ч406
Stieltjes series as asymptotic series 78 120Ч123 143p 260
Stieltjes series, Borel sum of 406
Stieltjes series, Carleman condition 410 415p 416p
Stieltjes series, derivation of 77Ч78 260
Stieltjes series, differential equation for 77Ч78
Stieltjes series, error estimates for optimally truncated 123 124f
Stieltjes series, moment problem 410 414Ч415p
Stieltjes series, Pade approximants for 387Ч388 390t 404Ч410 415Ч416p
Stirling series, Bernoulli numbers and 242p
Stirling series, derivation of using difference equations 222Ч223 225Ч227
Stirling series, derivation of using LaplaceТs method 275Ч276 310p
Stirling series, derivation of using method of steepest descents 294Ч296
Stirling series, description of 218Ч220 575
Stirling series, error estimates for 242p
Stirling series, optimal asymptotic approximation for 221t 222 223f 224t 242p
Stirling series, Pade approximants for 388Ч389 391
Stirling series, Richardson extrapolation of 376 377t
Stirling series, Taylor series vs. 220 221t 222
Stirling series, use of, to find minimum of  222 222
Stokes lines, definition of 116 (see also УStokes phenomenonФ)
Stokes phenomenon for Airy functions 116Ч118
Stokes phenomenon for parabolic cylinder functions 117
Stokes phenomenon in WKB theory 541p
Stokes phenomenon, definition of 115Ч116
Stokes phenomenon, functional relations used to determine 130Ч133 143p
Stokes phenomenon, steepest-descents method used to determine 300Ч302 313Ч315p
Sturm Ч Liouville problem 29 35p 351 490Ч491 491f 492f 492t 540p
Subdominance in boundary-layer problems 429
Subdominance in LaplaceТs method 262Ч263 273Ч274
Subdominance in WKB problems 531 (see also УStokes phenomenonФ)
Subdominance, explanation of 115Ч118
Substitutions for solving difference equations 53
Substitutions for solving differential equations 23Ч24 151 156Ч157
Summation methods 368Ч415
Summation methods for convergent series 368Ч379 389Ч392'
Summation methods for divergent series 379Ч410
Summation methods, asymptotic summation of series 376 379 380t
Summation methods, Borel 381Ч382
Summation methods, Euler 381
Summation methods, generalized (two-point) Pade 393Ч394
Summation methods, generalized Shanks transformation 389Ч392
Summation methods, multiple-scale methods as 549
Summation methods, optimal asymptotic approximation 94Ч100 112 112f 122Ч124 124f 221Ч224 376 379 388 392
Summation methods, Pade 383Ч410
Summation methods, philosophy of 120 368 379Ч381
Summation methods, Richardson extrapolation 375Ч376 377t 378t
Summation methods, Shanks transformation 369Ч375
Summation methods, summation of leading secularities 547Ч549 (see also УSums asymptotic
Summing factor 39
Sums, asymptotic evaluation of 302Ч306
Sums, asymptotic evaluation of approximation by Riemann integrals 303Ч304
Sums, asymptotic evaluation of Euler Ч Maclaurin sum formula for 305Ч306 306t 315 379 411p
Sums, asymptotic evaluation of LaplaceТs method applied to 304Ч305
Sums, asymptotic evaluation of truncation of 303
SylvesterТs eliminant 352 354 366p
Systems of first-order differential equations, autonomous see УAutonomous systemsФ
Systems of first-order differential equations, equivalence of, to general nth-order differential equation 5
Systems of first-order differential equations, removing a singularity by conversion to 66
Tauberian theorems 127Ч128 145p
Taylor series at ordinary points 62 65Ч70 104
Taylor series for 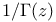 220 221t 222t 254f 255 385 387t 220 221t 222t 254f 255 385 387t
Taylor series for Airy functions 67Ч68 569
Taylor series for Bessel functions 143p
Taylor series for difference equations 210Ч212
Taylor series for digamma function 575
Taylor series for nonlinear differential equations 147Ч149
Taylor series for parabolic cylinder functions 574
Taylor series, asymptotic series vs. 90Ч91 92f 118Ч119 220 221t 222 254f 255
Taylor series, convergence of 90Ч91 92f
Taylor series, derivation of 252Ч253
Taylor series, leading asymptotic behaviors of 90Ч92 140p 304Ч305
Taylor series, near irregular singular points 65
Taylor series, near regular singular points 63 68Ч69
Taylor series, Pade approximants vs. 384Ч387 385Ч388t 400
Taylor series, perturbation series vs. 66 321Ч323 323f
Taylor series, Shanks transformation of 369Ч372 370t 371f
Taylor series, slowly converging 368Ч372
Taylor series, transients in 369Ч371
Thomas Ч Fermi equation 25Ч26 167Ч170 168Ч169t 170f 199Ч200p
Time scales, long and short 549 556 558Ч559
Time scales, multiple 551 564 567p
Toda lattice 187 188f 190 203p
Trajectories in phase space, almost periodic orbits 186Ч187 188f 189f
Trajectories in phase space, cycles 173f 175
Trajectories in phase space, definition of 172Ч173
Trajectories in phase space, global analysis of, in higher dimensions 185Ч197
Trajectories in phase space, global analysis of, in one dimension 174Ч175 176f
Trajectories in phase space, global analysis of, in two dimensions 175 178Ч183 468Ч470
Trajectories in phase space, global analysis of, using boundary-layer theory 468Ч479 476Ч478f 483p
Trajectories in phase space, limit cycles 183 184f 468Ч479 476Ч478f 483p 544Ч556 556f 557f
Trajectories in phase space, local analysis of, near critical points in higher dimensions 185Ч197
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -function
-function