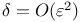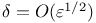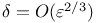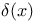|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bender C., Orszag S. Ч Advanced Mathematical Methods for Scientists and Engineers |
|
|
 |
| ѕредметный указатель |
 , calculation of 246p 411p , calculation of 246p 411p
Abel equation 34p
Abel formula for Wronskian for difference equations 42 43
Abel formula for Wronskian for differential equations 9 32p 33p
Abelian theorems 127
Airy equation, differential equation 13 151 156 506 569
Airy equation, eigenvalue problem for 28 521Ч522
Airy equation, inhomogeneous 105 106f 141Ч142p
Airy equation, local analysis, 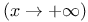 100Ч102 494Ч495 100Ч102 494Ч495
Airy equation, local analysis, 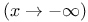 107Ч111 107Ч111
Airy equation, local analysis, 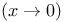 67Ч68 67Ч68
Airy equation, Stokes lines for 116Ч118 130Ч131
Airy functions Ai and Bi as Bessel functions 569
Airy functions Ai and Bi in one-turning-point problems 506Ч510 515Ч518 529Ч530 535Ч536
Airy functions Ai and Bi, asymptotic series, 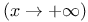 100Ч102 100Ч102
Airy functions Ai and Bi, asymptotic series, 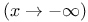 109Ч111 109Ч111
Airy functions Ai and Bi, asymptotic series, 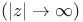 133Ч135 142p 570 133Ч135 142p 570
Airy functions Ai and Bi, definition of 68 69f
Airy functions Ai and Bi, functional relations for 131 569
Airy functions Ai and Bi, integral representations of 313Ч314p 570
Airy functions Ai and Bi, integrals of, behavior 256Ч258 308p 309p 364p
Airy functions Ai and Bi, leading asymptotic behaviors, 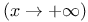 100 101f 102 100 101f 102
Airy functions Ai and Bi, leading asymptotic behaviors, 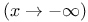 107Ч108 108f 109f 107Ч108 108f 109f
Airy functions Ai and Bi, leading asymptotic behaviors, 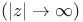 113Ч117 133Ч135 113Ч117 133Ч135
Airy functions Ai and Bi, sector of validity for Bi 115 115f
Airy functions Ai and Bi, Stokes behavior of 130Ч131 313Ч314p
Airy functions Ai and Bi, Taylor series for 67Ч68 569
Almost periodic orbits 186Ч187 188f 189f
Anharmonic oscillator, classical (DuffingТs equation) 545Ч551 547f 551f 566Ч567p
Anharmonic oscillator, quantum 334Ч335 337Ч338 353 353t 359Ч360 366Ч367p
Anti-Stokes lines 116 (See also УStokes linesФ)
Antiderivative, continuous 3
Antiderivative, discrete 37 53p 54p
Approximants 381 (See also УPade approximantsФ)
Arnold Ч Moser theorem 189 191
Asymptotic expansions see УAsymptotic seriesФ
Asymptotic matching for boundary-layer problems 421Ч483
Asymptotic matching for integrals 341Ч349 365Ч366p 515Ч519
Asymptotic matching for nonlinear differential equations 421Ч423 463Ч479
Asymptotic matching for nonlinear differential equations for WKB problems 504Ч543
Asymptotic matching for nonlinear differential equations, patching vs. 335Ч336 499
Asymptotic matching for nonlinear differential equations, principle of 335Ч336
Asymptotic matching for nonlinear differential equations, techniques of, for differential equations 336Ч341
Asymptotic matching, existence of matching region 428Ч430
Asymptotic matching, high-order 337 344Ч349 428Ч435 434Ч437f 438Ч452 442Ч444f 449f 478Ч479 535Ч536
Asymptotic power series see УAsymptotic seriesФ
Asymptotic relations (asymptotic order relations) for functions with noncoincident zeros 108Ч109
Asymptotic relations (asymptotic order relations) for oscillatory functions 107Ч112
Asymptotic relations (asymptotic order relations) in complex plane 112Ч118
Asymptotic relations (asymptotic order relations), definition of, 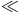 78Ч79 78Ч79
Asymptotic relations (asymptotic order relations), definition of,  78Ч79 78Ч79
Asymptotic relations (asymptotic order relations), definition of, O 318
Asymptotic relations (asymptotic order relations), differentiation of 127Ч128 145p
Asymptotic relations (asymptotic order relations), integration of 81 139p 142p
Asymptotic relations (asymptotic order relations), sector of validity for 113Ч118
Asymptotic relations (asymptotic order relations), Stokes phenomenon and subdominance 115Ч118
Asymptotic series for Airy functions 100Ч102 109Ч111 133Ч135 142p 570
Asymptotic series for Bessel functions 111Ч112 112f 228Ч229 294 572Ч573
Asymptotic series for digamma function 309p 575
Asymptotic series for exponential integrals 576
Asymptotic series for Fourier integrals 276Ч277 281Ч287
Asymptotic series for logarithmic integral function 310p
Asymptotic series for modified Bessel functions 93Ч94 144p 265 571
Asymptotic series, arithmetical operations on 125Ч126
Asymptotic series, construction of analytic function asymptotic to 144p
Asymptotic series, construction of continuous function asymptotic to 119Ч120 119f
Asymptotic series, convergent and divergent 118Ч120
Asymptotic series, definition of 89 118
Asymptotic series, derived by integration by parts 252Ч261 276Ч277
Asymptotic series, derived by LaplaceТs method and WatsonТs lemma 262Ч265
Asymptotic series, derived by steepest-descents method 281Ч287 294
Asymptotic series, derived from difference equations 218Ч219 225Ч231
Asymptotic series, derived from linear differential equations 84Ч87 90Ч94 98Ч101 104Ч105 109Ч111 129 133Ч136
Asymptotic series, derived from nonlinear differential equations 150 154Ч155 157Ч158 165Ч167
Asymptotic series, differentiation of 127Ч128
Asymptotic series, equating coefficients in 125
Asymptotic series, integration of 126
Asymptotic series, nonuniqueness of (subdominance) 123Ч124
Asymptotic series, optimal asymptotic approximation for 94Ч102 122Ч124 222 223f 224t 242
Asymptotic series, pfor parabolic cylinder functions 98Ч100 131Ч133 265 574
Asymptotic series, proof of existence of 128Ч129 133Ч136 144
Asymptotic series, Stieltjes series as 78 120Ч123 260
Asymptotic series, Stirling series for gamma function 218Ч220
Asymptotic series, Taylor series vs. 90Ч91 92f 118Ч119 220 221t 222 254f 255
Asymptotic series, uniqueness of coefficients 89Ч90 124Ч125
Asymptotic summation of series 376 379 380t
Autonomous equations, definition of 24
Autonomous equations, reduction of order for 24Ч26 156
Autonomous systems 171Ч197
Autonomous systems with almost periodic orbits 186Ч187 188f 189f
Autonomous systems, C-systems 192Ч193 204p
Autonomous systems, critical points of 173Ч177
Autonomous systems, definition of 171
Autonomous systems, DuffingТs equation 546 547f
Autonomous systems, Hamiltonian 189Ч191 189f 190f 204p
Autonomous systems, Henon and Heiles, example of 188Ч190 189f 190f
Autonomous systems, higher-dimensional 185Ч197
Autonomous systems, linear 177Ч178
Autonomous systems, Lorenz model 194Ч195 194Ч197f 204p
Autonomous systems, one-dimensional 174Ч175
Autonomous systems, predator-prey 179Ч183 180Ч182f
Autonomous systems, random behavior in 188Ч189 190f 191f 192Ч195 195Ч197f
Autonomous systems, Rayleigh oscillator 468Ч479 476Ч478f 483p 554Ч556 556f 557f
Autonomous systems, Toda lattice 187 188f 190 203p
Autonomous systems, two-dimensional 175Ч185 468Ч479 546Ч547
Autonomous systems, Van der Pol equation 202p 483p 567p
Averaging, method of 566p
Bernoulli equations, difference 57p
Bernoulli equations, differential 20 21 24
Bernoulli numbers 242p 305 306 314p 379
Bernoulli polynomials 305 315p
BernoulliТs method for finding roots of a polynomial 241p
Bessel equation, differential equation 14 111Ч112 143p 572
Bessel equation, differential equations equivalent to 322 573
Bessel equation, local analysis 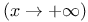 111Ч112 111Ч112
Bessel equation, modified see УModified Bessel equationФ
Bessel functions  and and 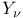 , Airy functions as 569 , Airy functions as 569
Bessel functions  and and 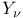 , asymptotic series, , asymptotic series, 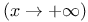 111Ч112 112f294 111Ч112 112f294
Bessel functions  and and 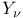 , asymptotic series, , asymptotic series, 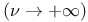 228Ч229 230t 228Ч229 230t
Bessel functions  and and 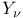 , asymptotic series, , asymptotic series, 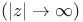 572Ч573 572Ч573
Bessel functions  and and 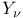 , difference equation for 55p 228 243p 573 , difference equation for 55p 228 243p 573
Bessel functions  and and 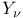 , differential equations for 322 572 573 , differential equations for 322 572 573
Bessel functions  and and 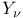 , Frobenius series for 572 , Frobenius series for 572
Bessel functions  and and 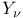 , functional relations for 143p 572 , functional relations for 143p 572
Bessel functions  and and 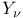 , generating function for 55p 573 , generating function for 55p 573
Bessel functions  and and 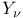 , integral representation for 280 291 293 298 309p 312p 573 , integral representation for 280 291 293 298 309p 312p 573
Bessel functions  and and 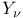 , leading asymptotic behaviors, , leading asymptotic behaviors, 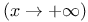 111 291 293Ч294 309p 111 291 293Ч294 309p
Bessel functions  and and 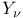 , leading asymptotic behaviors, ( , leading asymptotic behaviors, (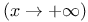 and and 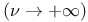 ) 280 298Ч299 312p ) 280 298Ч299 312p
Bessel functions  and and 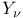 , modified see УModified Bessel functionsФ , modified see УModified Bessel functionsФ
Bessel functions  and and 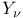 , optimal asymptotic approximation to , optimal asymptotic approximation to 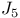 112 112f 113t 112 112f 113t
Bessel functions  and and 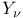 , Taylor series for 143p , Taylor series for 143p
Bessel functions  and and 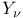 , uniform WKB approximation to 541p , uniform WKB approximation to 541p
Binomial theorem 204f 419
Blasius equation 34p
Borel summation 381Ч383 406 412p
Borel summation, generalized 382
Boundary layers, absence of 452
Boundary layers, definition of 326 327f 419Ч420 420f
Boundary layers, internal 455Ч463 466Ч468 469Ч475f 485 541Ч542p
Boundary layers, local breakdown at 484Ч485
Boundary layers, location of 425Ч426
Boundary layers, mathematical structure of 426Ч430
Boundary layers, multiple 437Ч438 439f" 440f" 446Ч455 449f" 458Ч460 464Ч475 465f 467Ч478f 485
Boundary layers, nested 453Ч455 481p
Boundary layers, thicknesses of 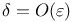 420 426 431 450 454 463 473 477 420 426 431 450 454 463 473 477
Boundary layers, thicknesses of 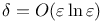 421 421
Boundary layers, thicknesses of 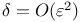 453 454 453 454
Boundary layers, thicknesses of 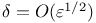 437Ч439 442Ч443 447 456 465 466 437Ч439 442Ч443 447 456 465 466
Boundary layers, thicknesses of 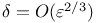 479 480p 479 480p
Boundary layers, thicknesses of how to determine 435Ч437
| Boundary-layer problems with coordinate singularity 452Ч453
Boundary-layer problems, absence of boundary layers 452
Boundary-layer problems, CarrierТs problem 464Ч475
Boundary-layer problems, exactly-soluble 326 327f 419Ч420 426Ч430
Boundary-layer problems, internal 455Ч463 466Ч475 541Ч542p
Boundary-layer problems, limit cycle of Rayleigh oscillator 468Ч479 483p
Boundary-layer problems, linear, fourth-order 449Ч452
Boundary-layer problems, linear, second-order 326 327f; 424f; 488Ч490 559Ч560
Boundary-layer problems, linear, third-order 446Ч449
Boundary-layer problems, mathematical structure of 426Ч430
Boundary-layer problems, nonlinear, first-order 421Ч422 422f 423f
Boundary-layer problems, nonlinear, second-order 463Ч479 483p
Boundary-layer theory 417Ч483
Boundary-layer theory as singular perturbation theory 326 430
Boundary-layer theory for nonlinear equations 421Ч422 422Ч423f 463Ч479 483p
Boundary-layer theory in higher order 428Ч435 434Ч437f 440Ч452 442Ч444f 449f 478Ч479
Boundary-layer theory with underdetermined or overdetermined solutions 461Ч467 465f 467Ч475f 482p
Boundary-layer theory, failure of 461Ч463 467 485 487
Boundary-layer theory, inner, outer, and intermediate limits in 426Ч430
Boundary-layer theory, internal boundary layers 455Ч463 466Ч475
Boundary-layer theory, introductory discussion 326 327f 417Ч426
Boundary-layer theory, multiple-scale theory vs. 559Ч560
Boundary-layer theory, uniform approximation in 425 430 433
Boundary-layer theory, WKB theory vs. 484Ч485 488Ч490 498 503Ч505
Boundary-value problems, for difference equations, eigenvalue 47Ч49 56p 231Ч233
Boundary-value problems, for difference equations, linear 39Ч40
Boundary-value problems, for difference equations, local analysis of 231Ч233
Boundary-value problems, for difference equations, well-posed 43 55p
Boundary-value problems, for differential equations, asymptotic matching for 336Ч341
Boundary-value problems, for differential equations, boundary-layer structure in linear 326 327f 419Ч420 422Ч463 488Ч490
Boundary-value problems, for differential equations, boundary-layer structure in nonlinear 463Ч479
Boundary-value problems, for differential equations, definition of 6Ч7
Boundary-value problems, for differential equations, eigenvalue see УEigenvalue problemsФ
Boundary-value problems, for differential equations, existence and uniqueness of solutions to 7 10Ч11
Boundary-value problems, for differential equations, GreenТs function solution of 19
Boundary-value problems, for differential equations, local analysis of linear 133 248
Boundary-value problems, for differential equations, local analysis of nonlinear 167Ч172
Boundary-value problems, for differential equations, multiple-scale analysis of 559Ч560
Boundary-value problems, for differential equations, patching used to solve 335Ч336
Boundary-value problems, for differential equations, well-posed 10Ч11
Boundary-value problems, for differential equations, WKB analysis of 326Ч327 328f 485 487Ч492 497Ч505 511 511Ч514f 518t 519Ч523 537Ч539
C-systems 192Ч193 204p
Carleman condition 410 415p 416p
Carlini Ч Green Ч Liouville approximation see УExponential substitutionФ
Casoratian see УWronskianФ
Centers, almost periodic behavior near 186Ч187 188f 189f
Centers, higher-dimensional 186Ч188
Centers, random behavior near 188Ч189 190f 191f 192Ч195 195Ч197f
Centers, random behavior near spurious 184Ч185
Centers, two-dimensional 173f 177Ч179 185
Completeness 351
Complex plane, asymptotic relations in 112Ч118
Complex plane, asymptotic series in 130Ч136
Complex plane, differential equations in 29Ч30
Complex plane, Pade approximants in 383Ч410
Complex plane, physical optics approximation in 54lp 542p
Complex plane, spontaneous singular points in 149
Complex plane, steepest descents, method of, in 280Ч302
Complex plane, WKB theory in 54lp 542p
Connection formulas 509 511Ч513 529Ч530
Constant-coefficient equations, difference 40Ч41 54Ч55p
Constant-coefficient equations, differential 11Ч12 32p 545
Constant-phase paths 282Ч287 (See also УSteepest descents method
Constants of integration 3 5Ч6
Constants of summation 37 38
Continued fractions for Stieltjes function 396 406Ч407
Continued fractions, algorithm for computing coefficients of 397Ч398
Continued fractions, algorithm for evaluating 398Ч399
Continued fractions, definition of 395
Continued fractions, examples of 395Ч396 413p
Continued fractions, Pade approximants and 396Ч398
Continued function representations, algorithms for computing 399Ч400 413p
Continued function representations, exponentials 147 196p 399 413p 414p
Continued function representations, fractions 395Ч400 413p
Continued function representations, logarithms 399 413p 414p
Continued function representations, square roots 245p 399 413p
Controlling factors, from difference equations of gamma function 223
Controlling factors, from difference equations, controlling factors of differential equations vs. 214Ч215
Controlling factors, from difference equations, dominant-balance method used to find 209 214 218 229 232Ч233
Controlling factors, from difference equations, methods for finding 214Ч218
Controlling factors, from differential equations see УLeading asymptotic behaviors; Dominant balance method
Controlling factors, from differential equations, definition of 79Ч80
Controlling factors, from differential equations, exponential substitution used to find 80Ч81 84 87 88 90Ч91 97
Controlling factors, from differential equations, geometrical optics approximation and 494
Convergence, acceleration of 369Ч376
Convergence, acceleration of, asymptotic summation of series 376 379 380t
Convergence, acceleration of, generalized Shanks transformation 389Ч392
Convergence, acceleration of, Richardson extrapolation 375Ч376 377t 378t
Convergence, acceleration of, Shanks transformation 369Ч375
CramerТs Rule 9 352
Critical points in phase space, centers 173f 177Ч179 180f 185Ч188
Critical points in phase space, definition of 173
Critical points in phase space, nodes 174Ч175 174f 176 177 181 182f 186 187f
Critical points in phase space, saddle points 174Ч175 174f 177 179Ч182 180Ч182f
Critical points in phase space, spiral points 176Ч179 181Ч184 181f 182f 184f 192Ч194f
Critical points in phase space, stability of 174Ч177 186 189 191
Critical-point analysis in phase space, one-dimensional 174Ч176
Critical-point analysis of C-systems 192Ч193 204p
Critical-point analysis of Hamiltonian systems 189Ч191 204p
Critical-point analysis of random systems 193Ч195 204p
Critical-point analysis of random systems, higher-dimensional 185Ч197 (See also УAutonomous systems; Critical pointsФ)
Critical-point analysis of random systems, two-dimensional 175Ч183
Critical-point analysis, Arnold Ч Moser theorem 189 191
Critical-point analysis, energy integrals used in 185
Critical-point analysis, failure of linear 183Ч185
Critical-point analysis, linear 174Ч183
Crossing of eigenvalues see УLevel crossingФ
Crossing of roots of polynomials 328Ч329 330f 331f 332f 363p
Cycles for difference equations 238 246p
Cycles in phase space 173f 175
Delta function 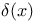 16 32p 310p 498 526Ч527 540Ч541p 16 32p 310p 498 526Ч527 540Ч541p
Delta function potential 526Ч527
Determinants for Pade approximants 384 391
Determinants of N x N matrices 352Ч355 366p
Determinants of solutions to differential and difference equations 8Ч9 11 32p 41Ч42
Determinants, difference equations used to compute 55Ч56p 366p
Determinants, Hill 352
Determinants, Wronskian see УWronskianФ
Difference calculus 36Ч37 207 211 214Ч216
Difference equations for Bessel functions 55p 228 243p 573
Difference equations for computing determinants 55Ч56p 366p
Difference equations for digamma function 214 575
Difference equations for exponential integrals 576
Difference equations for exponential integrals for gamma function 38 223 575
Difference equations for exponential integrals, factor linear difference operators 55p
Difference equations for exponential integrals, Fibonacci numbers 56p
Difference equations for exponential integrals, first-order linear 38Ч40
Difference equations for exponential integrals, for Hermite polynomials 55p 244p
Difference equations for exponential integrals, for Laguerre polynomials 244p
Difference equations for exponential integrals, for Legendre polynomials 55p 229
Difference equations for exponential integrals, for modified Bessel functions 571
Difference equations for exponential integrals, for parabolic cylinder functions 574
Difference equations for exponential integrals, Frobenius series for 212Ч214
Difference equations for exponential integrals, functional relations used to solve 40 53 56p 57p
Difference equations for exponential integrals, general solution of 38
Difference equations for exponential integrals, generating functions for 46Ч47 53 55p 572 573
Difference equations for exponential integrals, homogeneous linear see УHomogeneous linear difference equationsФ
Difference equations for exponential integrals, inhomogeneous linear see УInhomogeneous linear difference equationsФ
Difference equations for exponential integrals, initial-value problems 43 248Ч249
Difference equations for exponential integrals, integral representations for solutions to 248Ч249
Difference equations for exponential integrals, leading asymptotic behaviors from 207Ч210 223 225 227Ч239 248Ч249
Difference equations for exponential integrals, local analysis of linear 205Ч233 248Ч249
Difference equations for exponential integrals, local analysis of nonlinear 233Ч239
Difference equations for exponential integrals, NewtonТs method 234Ч235 244p 245p
Difference equations for exponential integrals, nonlinear local analysis of 233Ч239
Difference equations for exponential integrals, nonlinear methods for solving 40 53 56Ч57p
Difference equations for exponential integrals, ordinary, regular singular, and irregular singular points of 206Ч207
Difference equations for exponential integrals, periodic behavior of 238 246p
Difference equations for exponential integrals, random behavior of 237Ч239 239f
Difference equations for exponential integrals, reduction of order of 43Ч46 51Ч52 55p 56p
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 , calculation of
, calculation of 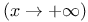
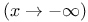
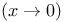
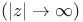

 and
and  , Airy functions as
, Airy functions as