|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bender C., Orszag S. — Advanced Mathematical Methods for Scientists and Engineers |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Difference equations for exponential integrals, substitution for solving 53
Difference equations for exponential integrals, summing factor 39
Difference equations for exponential integrals, Taylor series for 210—212
Difference equations for exponential integrals, undetermined coefficients, method of, for 52—53 56p
Difference equations for exponential integrals, variation of parameters 49—51 56p
Difference equations for exponential integrals, Wronskian (Casoratian) 41—43 55p
Difference equations, asymptotic expansions of solutions of 225—231
Difference equations, Bernoulli 57p
Difference equations, boundary-value problems 39—40 43 47—49 55p 56p 231—233
Difference equations, classification of the point at 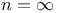 206—207 206—207
Difference equations, constant-coefficient 40—41 54—55p
Difference equations, constants of summation 37 38
Difference equations, controlling factors from 209 214—218 223 229 232—233
Difference equations, definitions of 37—38 40 49
Difference equations, difference calculus for 36—37 207 211 214—216
Difference equations, differential equations vs. 36 49 205—210 214—215 237
Difference equations, eigenvalue 47—49 56p 231—233
Difference equations, Euler 44—46 55p
Differential equations in complex plane 29—30
Differential equations, asymptotic matching for, techniques of 336—341
Differential equations, boundary-layer theory for 419—483
Differential equations, boundary-value problems see “Boundary-value problems”
Differential equations, constants of integration 3 5—6
Differential equations, controlling factors from 79—81 84 87 88 90—91 97 494
Differential equations, definitions of 3 4
Differential equations, eigenvalue problems see “Eigenvalue problems”
Differential equations, existence and uniqueness theorems 6—7 30—3lp 33p 196p
Differential equations, general solutions of 3 8 152—154
Differential equations, global analysis of 417—568
Differential equations, initial-value problems see “Initial-value problems”
Differential equations, integral representations for solutions to see “Integral representations”
Differential equations, leading asymptotic behaviors from see “Leading asymptotic behaviors”
Differential equations, local analysis of linear 61—145
Differential equations, local analysis of nonlinear 146—204
Differential equations, multiple-scale perturbation theory for 544—568
Differential equations, patching 335—336 505 527
Differential equations, periodic behavior see “Oscillators; Periodic behaviors”
Differential equations, perturbation techniques (elementary) for 321—324 326—341
Differential equations, random behavior of 188—197
Differential equations, singular points of see “Singular points”
Differential equations, systems of 5 66 171—197
Differential equations, WKB theory for 484—543 (See also “Linear differential equations; Nonlinear differential equations”)
Digamma function 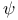 213—214 241p 242p 309p 575 576 213—214 241p 242p 309p 575 576
Dirac delta function see “Delta function”
Discrete derivative D 36 207 211 213 215 216
Dispersive phenomena 484—486 (See also “WKB theory”)
Dissipative phenomena 484—486 (See also “Boundary-layer theory”)
Distinguished limits 435—446
Distinguished limits in boundary-layer theory 435—438 441 443 447 450 453 454 456 465 473 479
Distinguished limits in WKB theory 486 488
Distinguished limits, absence of 452
Distinguished limits, explanation of 435—437
Dominance 115 (See also “Subdominance”)
Dominant balance, method of controlling factors of difference equations found by 208—209 214 218 229 232—233
Dominant balance, method of corrections to leading behaviors found by 84—87
Dominant balance, method of discussion of 83—84 208—209 235—237
Dominant balance, method of distinguished limits found by see “Distinguished limits”
Dominant balance, method of failure of 208 235—237
Dominant balance, method of three-term 106—107 14
Dominant balance, method of, for inhomogeneous linear differential equations 104—107 141p
Dorodnicyn formula for period of Rayleigh oscillator 477—479
Duffing’s equation 545—551 547f 551.f; 566—567p
Dunham’s generalization of WKB eigenvalue condition 537
e, calculation of 411p
Eigenfunctions of difference equations 48 56p
Eigenfunctions, completeness 351
Eigenfunctions, definition of 27
Eigenfunctions, expansion in terms of 351—352
Eigenfunctions, normalization of 29 490
Eigenfunctions, orthogonality of 29 48 56p 490
Eigenfunctions, WKB approximation to 490—491 491f 492f 524—526f
Eigenvalue condition, WKB 467 519—523 537—539
Eigenvalue problems for differential equations, asymptotic matching for 338—341
Eigenvalue problems for differential equations, elementary examples of 27—29 35p
Eigenvalue problems for differential equations, mathematical structure of perturbative 350—361
Eigenvalue problems for differential equations, nonlinear 338—341
Eigenvalue problems for differential equations, perturbative treatment of 330—335 338—341
Eigenvalue problems for differential equations, Schrodinger equation see Schrodinger equation
Eigenvalue problems for differential equations, Sturm — Liouville see “Sturm — Liouville problem”
Eigenvalue problems for differential equations, WKB analysis of 490—492 519—523 523t 524—526f 537—539 542p 543p
Eigenvalue problems, for difference equations 47—49 56p 231—233
Eikonal equation 487
Elliptic functions 158 161 246p
Emden equation (Prob. 1.37) 35p
Energy eigenvalue, defined 331 (See also “Schrodinger equation”)
Energy integrals 185 193 546 552—553
Equidimensional (Euler) differential equations, linear 12
Equidimensional (Euler) differential equations, nonlinear 4 25 27 156
Euler difference equations 44—46 55p
Euler differential equations see “Equidimensional differential equations”
Euler summation 381 383 412p
Euler — Maclaurin sum formula 305—306 306t 315p 379 411p
Eulerian wobble 202—203p 203f 204f
Euler’s constant y 252 281 306 307p 316p 342 411p 575p
exact equations 13 23 33p
Existence and uniqueness theorems 6—7 30—31p 33p 196p
Exponential approximation see “Exponential substitution”
Exponential integrals 252 483p 575—576
Exponential substitution, for difference equations 214 216—217
Exponential substitution, for differential equations as basis for approximation methods 493
Exponential substitution, for differential equations in WKB theory 485—486
Exponential substitution, for differential equations, finding controlling factors using 80—81 87 88 90—91 97
Factorial function see “Gamma function”
Factoring, linear difference operators 55p
Factoring, linear differential operators 22 33p 34p
Fibonacci numbers 56p
Fixed singular points 146 158
Floquet theory 560—561 568p
Fourier integrals, asymptotic expansion of using asymptotic matching 347—349
Fourier integrals, asymptotic expansion of using integration by parts 276—278 311p
Fourier integrals, asymptotic expansion of using method-of steepest descents 281—287 291 293—294
Fourier integrals, conversion into Laplace integrals 281
Fourier integrals, definition of ordinary and generalized 276
Fourier integrals, Fresnel integral 308p
Fourier integrals, leading asymptotic behavior 278—280
Fourier integrals, Riemann — Lebesgue lemma for 277—278 285 31
Frequency shift 548 551 552f 553
Frequency, natural 544
Fresnel integral 308p
Frobenius series, for difference equations 212—214
Frobenius series, for differential equations at irregular singular points 77—78
Frobenius series, for differential equations at ordinary points 73
Frobenius series, for differential equations at regular singular points 68—76 452
Frobenius series, for differential equations for Bessel functions 572
Frobenius series, for differential equations for exponential integrals 252 576
Frobenius series, for differential equations for higher-order equations 76 138p
Frobenius series, for differential equations for incomplete gamma function 251—252 344—347 365p
Frobenius series, for differential equations for modified Bessel functions 71 74. 342 570—571
Frobenius series, for differential equations, controlling factor and leading behavior of 80
Frobenius series, for differential equations, definition of 69
Frobenius series, for differential equations, differentiation of, with respect to indicial exponents 73—76
Frobenius series, for differential equations, indicial exponents for 63 69—76 452
Frobenius series, for differential equations, indicial polynomial for 70 71 76
Fuchs, theorems of 62 63
Functional relations for Airy functions 131 569
Functional relations for Bessel functions 143p 572
Functional relations for gamma function 575
Functional relations for modified Bessel functions 143p 571
Functional relations for parabolic cylinder functions 132 574
Functional relations for probability density 238 245p
Functional relations, difference equations solved by 40 53 56p 57p
Galerkin method 352
Gamma function 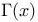 , definition and properties of 38 39f 54p 574—575 , definition and properties of 38 39f 54p 574—575
Gamma function 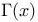 , difference equation for 38 223 575 , difference equation for 38 223 575
Gamma function 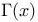 , digamma function see “Digamma function” , digamma function see “Digamma function”
Gamma function 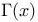 , incomplete 251—252 344—346 365—366p , incomplete 251—252 344—346 365—366p
Gamma function 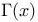 , integral representation for 38 54p 248 275 295 574 , integral representation for 38 54p 248 275 295 574
Gamma function 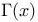 , Stirling series for see “Stirling series” , Stirling series for see “Stirling series”
Gamma function 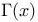 , Taylor series for 220 221f 222t 254f 255 385 387t , Taylor series for 220 221f 222t 254f 255 385 387t
Gamma function 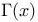 , use in Taylor and Frobenius series for difference equations 211—214 , use in Taylor and Frobenius series for difference equations 211—214
| Gaussian elimination 398
General solution of difference equations 38
General solution of differential equations 3 8 152—154
Generating functions for Bessel functions 55p 573
Generating functions for difference equations 46—47 53
Generating functions for Hermite polynomials 55p
Generating functions for Legendre polynomials 55p
Generating functions for modified Bessel functions 572
Geometrical optics approximation 494—495
Global analysis 317—367 417—568
Global analysis, asymptotic matching 335—349
Global analysis, boundary-layer theory 419—483
Global analysis, multiple-scale perturbation theory 544—568
Global analysis, perturbation series 319—367
Global analysis, philosophy of 6—7 59 317—318 417
Global analysis, WKB theory 484—543
Global breakdown 485
Green’s functions, boundary-value problems solved using 19 32p
Green’s functions, definition of 16—17
Green’s functions, variation of parameters vs. 18—19 498
Green’s functions, WKB approximation to 498—504 540—541
Hamiltonian systems 188—191 189f 190f 204p
Harmonic oscillator with aging spring 327—328 329f 568p
Harmonic oscillator, classical 544—545 548
Harmonic oscillator, damped 552—553 554f 555f
Harmonic oscillator, quantum 28 133 332—333 522—523 538
Heaviside step function 16—18
Herglotz function 357—359 366p 406 415p 416p
Hermite polynomials  in eigenfunctions of quantum harmonic oscillator 28 133 333 in eigenfunctions of quantum harmonic oscillator 28 133 333
Hermite polynomials  , behavior of , behavior of 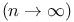 244p 244p
Hermite polynomials  , difference equation for 55p 244p , difference equation for 55p 244p
Hill determinant 352
Homogeneous linear difference equations, classification of the point at 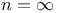 206—207 206—207
Homogeneous linear difference equations, Frobenius series for 212—214.
Homogeneous linear difference equations, general form of 40
Homogeneous linear difference equations, general solution of 42—43
Homogeneous linear difference equations, leading asymptotic behaviors from 207—210 223 225 227—233 248—249
Homogeneous linear difference equations, linear independence of solutions to 41—42 55p
Homogeneous linear difference equations, local analysis of 205—233
Homogeneous linear difference equations, reduction of order for 43—44 46 56p
Homogeneous linear difference equations, solution of general first-order 38—39
Homogeneous linear difference equations, Taylor series for 210—212
Homogeneous linear difference equations, Wronskian (Casoratian) for 41—43 55p
Homogeneous linear differential equations, classification of singular points of 62—66
Homogeneous linear differential equations, definition of 4
Homogeneous linear differential equations, general solution of 8
Homogeneous linear differential equations, linear independence of solutions of 8—9
Homogeneous linear differential equations, local behavior near irregular singular points of 76—103
Homogeneous linear differential equations, local behavior near ordinary points of 66—69
Homogeneous linear differential equations, local behavior near regular singular points of 68—76
Homogeneous linear differential equations, reduction of order of 13 32p
Homogeneous linear differential equations, theory of 7—11
Homogeneous linear differential equations, Wronskian 8—11 15 31p 32p
Hyperairy equation 102—103 143—144p 315p 497
Hypergeometric functions, continued-fraction representation for 396 413p
Hypergeometric functions, differential equation for 35p
Ill-posed see “Well-posed”
Incomplete gamma function  , ,  251—252 344—346 365—366p 251—252 344—346 365—366p
Indicial exponents for equidimensional equations 12
Indicial exponents for Frobenius series 63 69—76 452
Indicial polynomial 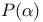 70—71 73—76 70—71 73—76
Inhomogeneous Airy equation 105 106f 141—142p
Inhomogeneous linear difference equations, general form of 49
Inhomogeneous linear difference equations, reduction of order for 51—52 55p 56p
Inhomogeneous linear difference equations, solution of general first-order 39—40
Inhomogeneous linear difference equations, undetermined coefficients, method of, for 52—53 56p
Inhomogeneous linear difference equations, variation of parameters for 49—51 56p
Inhomogeneous linear differential equations, appearance of, in perturbation theory 321—322
Inhomogeneous linear differential equations, definition of 4
Inhomogeneous linear differential equations, form of solution to 14
Inhomogeneous linear differential equations, Green’s functions for 16—19 32p
Inhomogeneous linear differential equations, local analysis of 103—107 141p
Inhomogeneous linear differential equations, reduction of order for 19 32p 333
Inhomogeneous linear differential equations, resonant and secular behavior of 544—549
Inhomogeneous linear differential equations, solution of arbitrary first-order 14
Inhomogeneous linear differential equations, undetermined coefficients, method of, for 19—20
Inhomogeneous linear differential equations, variation of parameters for 15 18—19 32p 103—104 20lp 498
Inhomogeneous linear differential equations, WKB solutions of 497—504 500—505f
Initial-value problems for difference equations 42—43 248—249
Initial-value problems for differential equations, asymptotic matching for 336—337 421—423
Initial-value problems for differential equations, boundary-layer structure in 421—423 480p
Initial-value problems for differential equations, definition and examples of 5—7
Initial-value problems for differential equations, existence and uniqueness theorems for 6—7 30—31p
Initial-value problems for differential equations, local analysis of linear 67—69 247—248
Initial-value problems for differential equations, local analysis of nonlinear 147—153 186—188
Initial-value problems for differential equations, multiple-scale analysis of linear 327—328 329f 556—566 568p
Initial-value problems for differential equations, multiple-scale analysis of nonlinear 545—556 566—567p
Initial-value problems for differential equations, regular perturbation theory solutions of 321—322 323f 327 329f
Initial-value problems for differential equations, well-posed 9—10
Initial-value problems for differential equations, WKB structure in linear 488 489f
Inner, approximation in boundary-layer theory 421—483
Inner, limit, defined 427
Inner, region, defined 342—343 420 420f
Inner, solution, in boundary-layer theory 421—483
Inner, variables, defined 427 (See also “Boundary-layer theory”)
Integral representations for Airy functions 313—314f7 570
Integral representations for Bessel functions 280 291 293 298 309p 312p 573
Integral representations for difference equation solutions 248—249
Integral representations for digamma function 309p
Integral representations for Euler’s constant 252 281 307p
Integral representations for exponential integrals 252 483p 575
Integral representations for gamma function 38 54p 248 275 295 574
Integral representations for hyperairy function 315p 574
Integral representations for incomplete gamma function 251
Integral representations for Legendre polynomials 309p
Integral representations for logarithmic integral function 310p
Integral representations for modified Bessel functions 268 270 313p 571
Integral representations for moments 121—122 405
Integral representations for parabolic cylinder functions 315p
Integral representations for Riemann sums 303
Integral representations, Fourier integral 278
Integral representations, Fresnel integral 308p
Integral representations, general discussion 247—249
Integral representations, generalized Fourier integral 278
Integral representations, Laplace integrals 258—259
Integral representations, Stieltjes integral 120—122
Integrals, asymptotic expansion of 247—316
Integrals, asymptotic expansion of WKB approximation 490—491 500—504 513—519 540—54lp
Integrals, asymptotic expansion of, asymptotic matching for 341—349 365—366p 515—519
Integrals, asymptotic expansion of, elementary methods 249—252
Integrals, asymptotic expansion of, integration by parts 252—261 276—278 311p
Integrals, asymptotic expansion of, Laplace’s method 261—276 309—311p
Integrals, asymptotic expansion of, stationary phase, method of 276—280 311—312p
Integrals, asymptotic expansion of, steepest descents, method of 280—302
Integrating factors 13 14 23 34p
Integration by parts 252—261
Integration by parts for asymptotic expansion of integrals 252—261 348—349
Integration by parts for Fourier integrals 276—278 311p
Integration by parts for Laplace integrals 258—259
Integration by parts, failure of 259—261 281
Intermediate limits, definition of 428 (See also “Boundary-layer theory”)
Irregular singular points, of difference equations, asymptotic series about 255—231
Irregular singular points, of difference equations, controlling factors near 214—218 223
Irregular singular points, of difference equations, definition of 207
Irregular singular points, of difference equations, leading asymptotic behaviors near 223 225 227—233
Irregular singular points, of differential equations at  64 88—103 64 88—103
Irregular singular points, of differential equations, controlling factors near 79—81 84 87 88 90—91 97
Irregular singular points, of differential equations, definition of 63—64
Irregular singular points, of differential equations, Frobenius series near, failure of 77—78
Irregular singular points, of differential equations, leading asymptotic behavior near 79—88 90—92 96—97 100 102—103
Irregular singular points, of differential equations, local behavior near 76—103
Irregular singular points, of differential equations, Taylor series near 65
Iteration methods,  , calculation of 246p , calculation of 246p
Iteration methods, Bernoulli’s 241p
Iteration methods, continued exponentials 147
Iteration methods, continued square roots 245p
Iteration methods, Newton’s 234—235 244p 245p
Laguerre polynomials 244p
Langer’s uniform WKB approximation 510—511 541p
Laplace integrals, asymptotic expansion of 261—276
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



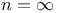
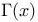 , definition and properties of
, definition and properties of  in eigenfunctions of quantum harmonic oscillator
in eigenfunctions of quantum harmonic oscillator 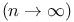
 ,
, 
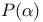

 , calculation of
, calculation of