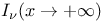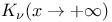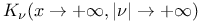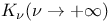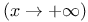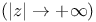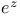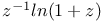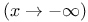|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bender C., Orszag S. — Advanced Mathematical Methods for Scientists and Engineers |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Laplace integrals, conversion of Fourier integrals into 281
Laplace integrals, definition of 258 261
Laplace integrals, integration by parts for 258—259
Laplace integrals, Watson’s lemma for 263—265 281 284
Laplace’s method 261—276
Laplace’s method for integrals with movable maxima 274—276 286 309—311p
Laplace’s method, applied to sums 304—305
Laplace’s method, approximation explained carefully 269—272 270f 271f
Laplace’s method, failure of 296—297 300
Laplace’s method, finding higher-order behaviors by 272—274 280
Laplace’s method, finding leading asymptotic behaviors by 261—263 266—272
Laplace’s method, Watson’s lemma 263—265 281 284
Leading asymptotic behaviors of Airy functions 100 101f 102f 107—108 108f 109f 113 115—117
Leading asymptotic behaviors of Bessel functions 111 280 291 293—294 298—299 309p 312p
Leading asymptotic behaviors of modified Bessel functions 91—92 92f 268 270—272 310p 313p
Leading asymptotic behaviors of Pade approximants 402—405
Leading asymptotic behaviors of parabolic cylinder functions 97 117 134—136 142—143p
Leading asymptotic behaviors of sums 303—305
Leading asymptotic behaviors of Taylor series 90—92 304—305
Leading asymptotic behaviors, comparison of, from difference and differential equations 207—210 214—216 237
Leading asymptotic behaviors, definition of 79—80
Leading asymptotic behaviors, derived by asymptotic matching 336—349
Leading asymptotic behaviors, derived by boundary-layer theory 422—423 425 437—440 455—477
Leading asymptotic behaviors, derived by elementary methods for integrals 249—250 253 258—259
Leading asymptotic behaviors, derived by Laplace’s method 262—263 266—272
Leading asymptotic behaviors, derived by multiple-scale analysis 548—560 563—564
Leading asymptotic behaviors, derived by stationary phase, method of 278—280 311—312p
Leading asymptotic behaviors, derived by steepest descents, method of 283 287 294—300
Leading asymptotic behaviors, derived by WKB theory (physical optics) 487—533
Leading asymptotic behaviors, derived from difference equations, effect of initial data on 248—249
Leading asymptotic behaviors, derived from difference equations, near irregular singular points 223—233
Leading asymptotic behaviors, derived from difference equations, near ordinary and regular singular points 207—210
Leading asymptotic behaviors, derived from difference equations, nonlinear 233—239
Leading asymptotic behaviors, derived from differential equations, effect of initial data on 247—248
Leading asymptotic behaviors, derived from differential equations, higher-order corrections to 84—87 92—94 96—102
Leading asymptotic behaviors, derived from differential equations, near irregular singular points 79—88 90—92 96—97 100 102—103
Leading asymptotic behaviors, derived from differential equations, nonlinear 149—152 154 157—158 166—167 171
Legendre polynomials 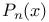 , behavior of , behavior of 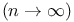 229 231 232t 309p 229 231 232t 309p
Legendre polynomials 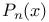 , difference equation for 55p 229 , difference equation for 55p 229
Legendre polynomials 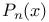 , differential equation for 243p , differential equation for 243p
Legendre polynomials 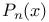 , generating function for 55p , generating function for 55p
Legendre polynomials 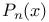 , integral representation for 309p , integral representation for 309p
Legendre polynomials 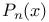 , zeros of 231 232t , zeros of 231 232t
Level crossing of eigenvalues for finite matrices 350
Level crossing of eigenvalues for Schrodinger equation eigenvalue problem 354—355 356—358f 360—361
Level crossing of eigenvalues, Simon, theorem by, on 363
Level curves 33p
Limit cycles in two dimensions 183 184f
Limit cycles of Rayleigh oscillator 468—479 476—478f 483p 554—556 556f 557f
Limit cycles of Van der Pol equation 483p 567p
Limit cycles, period of 476—479
Linear dependence see “Linear independence”
Linear difference equations see “Difference equations”
Linear differential equations, Airy 13 28 67—68 116—118 130—131 156 494—495 506 521—522 569
Linear differential equations, asymptotic matching for 336—341 (See also “Asymptotic matching”)
Linear differential equations, Bessel 14 111—112 143p 322 572 573
Linear differential equations, boundary-layer solutions of 419—463 479—482p
Linear differential equations, boundary-value problems for see “Boundary-value problems”
Linear differential equations, constant-coefficient 11—12 32p 545
Linear differential equations, controlling factors from see “Controlling factors”
Linear differential equations, definition of 3 4
Linear differential equations, eigenvalue-problems see “Eigenvalue problems”
Linear differential equations, equidimensional (Euler) 12 32p
Linear differential equations, exact 13
Linear differential equations, factoring linear differential operators 22 33p 34p
Linear differential equations, Floquet theory 560—561 568p
Linear differential equations, for Stieltjes function 77—78
Linear differential equations, Frobenius series for see “Frobenius series”
Linear differential equations, general solution of 8
Linear differential equations, Green’s functions 16—19 32p 498—504 540—541p
Linear differential equations, homogeneous see “Homogeneous linear differential equations”
Linear differential equations, hyperairy equation 102—103 143—144p 315p 497
Linear differential equations, hypergeometric 35p
Linear differential equations, inhomogeneous see “Inhomogeneous linear differential equations”
Linear differential equations, inhomogeneous Airy 105 106f 141—142p
Linear differential equations, initial-value problems for see “Initial-value problems”
Linear differential equations, integrating factors for 13 14
Linear differential equations, Langer’s uniform approximation 510—511 541p
Linear differential equations, leading asymptotic behaviors from see “Leading asymptotic behaviors”
Linear differential equations, Legendre 55p 229
Linear differential equations, local analysis of 61—145
Linear differential equations, Mathieu 339 560—566 568p
Linear differential equations, modified Bessel 92—96 570
Linear differential equations, multiple-scale perturbation theory for 556—566
Linear differential equations, ordinary, regular singular, and irregular singular points of see “Ordinary points; Singular points”
Linear differential equations, parabolic cylinder (Weber — Hermite) equation see “Parabolic cylinder equation”
Linear differential equations, patching 335—336 497—505 527
Linear differential equations, periodic behaviors of see “Oscillators; Periodic behaviors”
Linear differential equations, quantum anharmonic oscillator see “Anharmonic oscillator”
Linear differential equations, quantum harmonic oscillator see “Harmonic Oscillator”
Linear differential equations, reduction of order for 13 19 32p 333
Linear differential equations, resonant behavior of 544—545
Linear differential equations, scattering 524—533 542—543p
Linear differential equations, Schrodinger see “Schrodinger equation”
Linear differential equations, stability see “Stability”
Linear differential equations, Stokes phenomenon 115—118 130—133
Linear differential equations, Sturm — Liouville problem 29 35p 351 490—492 540p
Linear differential equations, systems of 66 177—178
Linear differential equations, Taylor series for see “Taylor series”
Linear differential equations, undetermined coefficients, method of, for 19—20
Linear differential equations, variation of parameters for 15 18—19 32p 103—104 201p 498
Linear differential equations, WKB theory for 484—543
Linear differential equations, Wronskian 8—11 15 31p 32p
Linear independence of continuous functions 8—9
Linear independence of discrete functions 41—42 55p
Linear independence, Wronskian test of 8 41—42 55p
Lipschitz condition 30 31
Local analysis 61—316
Local analysis of difference equations 205—246
Local analysis of integrals 247—316
Local analysis of linear differential equations 61—145
Local analysis of nonlinear differential equations 146—204
Local analysis of systems of differential equations 171—197
Local analysis, philosophy of 6—7 59 317—318 324 499
Local breakdown at boundary layers 484—485
Logarithmic integral function li (x) 310p
Logarithmic spirals 24 33p
Lorenz model 194—195 194—197f 204p
Matched asymptotic expansions see “Asymptotic matching”
Matching regions for one-turning point problems 506—508 (see also “Asymptotic matching”)
Matching regions, existence of 428—430
Matching regions, extent of, in higherrorder 336—339 342—349 432—433
Mathieu equation 339 560—566 568p
Matrix algebra, elementary techniques 177—178 201p
Modified Bessel equation, arbitrary order 92—96 570
Modified Bessel equation, half-odd integer order 73 93
Modified Bessel equation, imaginary order 340
Modified Bessel equation, integer order 74—76 90—91 92f
Modified Bessel equation, local analysis near 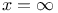 90—97 90—97
Modified Bessel equation, local analysis near x = 0 71 73—76
Modified Bessel functions  and and  as weight function in Stieltjes series 122 as weight function in Stieltjes series 122
Modified Bessel functions  and and  in asymptotic matching 340 455 in asymptotic matching 340 455
Modified Bessel functions  and and  , , leading asymptotic behaviors, , , leading asymptotic behaviors, 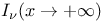 91 92f 270—272 310p 91 92f 270—272 310p
Modified Bessel functions  and and  , , leading asymptotic behaviors, , , leading asymptotic behaviors, 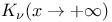 268 268
Modified Bessel functions  and and  , , leading asymptotic behaviors, , , leading asymptotic behaviors, 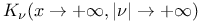 268 313p 268 313p
Modified Bessel functions  and and  , , leading asymptotic behaviors, , , leading asymptotic behaviors, 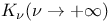 310p 310p
Modified Bessel functions  and and  , asymptotic series, , asymptotic series, 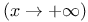 93—94 144p 265 93—94 144p 265
Modified Bessel functions  and and  , asymptotic series, , asymptotic series, 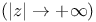 571 571
Modified Bessel functions  and and  , definitions of 71 74 , definitions of 71 74
Modified Bessel functions  and and  , difference equation for 571 , difference equation for 571
Modified Bessel functions  and and  , Frobenius series for , Frobenius series for  71 570 71 570
Modified Bessel functions  and and  , Frobenius series for for , Frobenius series for for 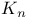 74 76 342 571 74 76 342 571
Modified Bessel functions  and and  , Frobenius series for for , Frobenius series for for  570 570
Modified Bessel functions  and and  , functional relations for 143p 571 , functional relations for 143p 571
Modified Bessel functions  and and  , generating function for 572 , generating function for 572
Modified Bessel functions  and and  , integral representations for 268 270 313p 571 , integral representations for 268 270 313p 571
Modified Bessel functions  and and  , optimal asymptotic approximations to 95 95t 96f 97f 243p , optimal asymptotic approximations to 95 95t 96f 97f 243p
Modified Bessel functions  and and  , proof of existence of asymptotic expansion for , proof of existence of asymptotic expansion for  129 145p 129 145p
Modified Bessel functions  and and  , Richardson extrapolation of recurrence relation for 376 378t , Richardson extrapolation of recurrence relation for 376 378t
Modified Bessel functions  and and  , Stokes phenomenon for 143p , Stokes phenomenon for 143p
| Moment integrals 121—122 405
Moment problem 410 414—415p
Movable maxima, Laplace’s method for 274—276 286 309—311p
Movable singular points see “Spontaneous singular points”
Multiple-scale perturbation problems, boundary-layer problem solved as 559—560
Multiple-scale perturbation problems, damped harmonic oscillator 552—553 554f 555f
Multiple-scale perturbation problems, Duffing’s equation 545—551 547f 551f 552f
Multiple-scale perturbation problems, harmonic oscillator with aging spring 327—328 329f
Multiple-scale perturbation problems, Mathieu equation 560—566 568p
Multiple-scale perturbation problems, oscillator with slowly varying frequency 556 558—559
Multiple-scale perturbation problems, Rayleigh oscillator 554—556 556f 557f
Multiple-scale perturbation theory 544—568
Multiple-scale perturbation theory, averaging, method of 566p
Multiple-scale perturbation theory, boundary-layer approximation derived by 559—560
Multiple-scale perturbation theory, failure of (Cheng and Wu example) 568p
Multiple-scale perturbation theory, formal procedures of 549—551
Multiple-scale perturbation theory, introductory discussion 327—328 329f 417 544
Multiple-scale perturbation theory, nonuniformity of regular perturbation expansions in 545—546
Multiple-scale perturbation theory, resonant and secular behavior 544—545
Multiple-scale perturbation theory, summation of leading secularities 547—549
Multiple-scale perturbation theory, time scales 549 551 556 558—559 564 567p
Multiple-scale perturbation theory, WKB approximation derived by 556 558—559
Natural frequency 544
Newton’s method 234—235 244p 245p
Nodes, one-dimensional 174—175 174f
Nodes, three-dimensional 186 187f
Nodes, two-dimensional 176—177 181 182f
Nonlinear difference equations see “Difference equations”
Nonlinear differential equations, Abel 34p
Nonlinear differential equations, Arnold — Moser theorem 189 191
Nonlinear differential equations, asymptotic matching for 421—423 463—479
Nonlinear differential equations, autonomous 24—26 156
Nonlinear differential equations, autonomous systems of 171—197 (see also “Autonomous systems; Critical point analysis”)
Nonlinear differential equations, Bernoulli 20 21 24
Nonlinear differential equations, Blasius 34p
Nonlinear differential equations, boundary-layer solutions of 421—423 463—479 483p
Nonlinear differential equations, boundary-value problems for see “Boundary-value problems”
Nonlinear differential equations, C-systems 192—193 204p
Nonlinear differential equations, critical points of 173—195
Nonlinear differential equations, Duffing’s 545—552 566—567p
Nonlinear differential equations, Emden (Prob. 1.37) 35p
Nonlinear differential equations, equidimensional (Euler) 4 25 27 156
Nonlinear differential equations, equivalence of, to a first-order system 5
Nonlinear differential equations, exact 23 33p
Nonlinear differential equations, general solution of 152—154
Nonlinear differential equations, Hamiltonian systems 189—191 204p
Nonlinear differential equations, Henon and Heiles, example of 188—190
Nonlinear differential equations, initial-value problems for see “Initial-value problems”
Nonlinear differential equations, integrating factors for 23 34p
Nonlinear differential equations, leading asymptotic behaviors from see “Leading asymptotic behaviors”
Nonlinear differential equations, local analysis of 146—204
Nonlinear differential equations, Lorenz model 194—197 204p
Nonlinear differential equations, multiple-scale perturbation theory for 545—557
Nonlinear differential equations, Painleve transcendents 158—165 198—199p
Nonlinear differential equations, periodic behavior of see “Oscillators; Periodic behaviors”
Nonlinear differential equations, Poincare plot 188—190
Nonlinear differential equations, predator-prey systems 179—183
Nonlinear differential equations, random behavior of 188—197
Nonlinear differential equations, Rayleigh oscillator 468—479 483p 554—557
Nonlinear differential equations, reduction of order for 24—27 34p 35p 156
Nonlinear differential equations, Riccati 4 20—22 27 34p 149—152 150f 152f 153t 156 197—198p
Nonlinear differential equations, scale-invariant 25—26 156
Nonlinear differential equations, separable 3 23 24 30p
Nonlinear differential equations, singular points of see “Singular points”
Nonlinear differential equations, stability and see “Stability”
Nonlinear differential equations, substitutions for solving 23—24 151 156—157
Nonlinear differential equations, Taylor series for see “Taylor series”
Nonlinear differential equations, Thomas-Fermi 25—26 167—170 168—169f 170f 199—200p
Nonlinear differential equations, Toda lattice 187—188 190 203p
Nonlinear differential equations, Van der Pol 202p 483p 567p
Nonuniformity of regular perturbation series 327—328 545—549
One-turning-point problems for first-order (simple) turning point 504—519 511—514f 529—530
One-turning-point problems for second-order turning point 532—533 541p
One-turning-point problems, connection formula 509 511—513 529—530
One-turning-point problems, higher-order WKB analysis of 534—536
One-turning-point problems, normalization of solution to 513—519
One-turning-point problems, two-turning-point problems derived from 519—520 530—531
One-turning-point problems, uniform asymptotic approximation for 510—511
One-turning-point problems, validity of WKB approximation for 506—508
Optimal asymptotic approximations for Bessel functions 112 112f 113
Optimal asymptotic approximations for modified Bessel functions 94—96 95f 96f 97f 243p
Optimal asymptotic approximations for parabolic cylinder functions 98f 99—100 99f 100 243p
Optimal asymptotic approximations for Riemann zeta function 376 379 380t
Optimal asymptotic approximations for Stirling series 221t 222 223f 224t 242p
Optimal asymptotic approximations, definition of 94
Optimal asymptotic approximations, error estimates for 123 124f
Optimal asymptotic approximations, Pade approximants vs. 388—392
Optimal asymptotic approximations, use of 94—100 122—124 124f
Ordinary points of difference equations, definition of 207
Ordinary points of difference equations, leading asymptotic behavior near 207—210
Ordinary points of difference equations, Taylor series near 210—212
Ordinary points of differential equations at  64 64
Ordinary points of differential equations, definition of 62
Ordinary points of differential equations, Frobenius series near 73
Ordinary points of differential equations, Taylor series near 62 65—70
Orthogonal families of curves 33p
Oscillators with slowly varying frequency 556 558—559 568p
Oscillators, anharmonic see “Anharmonic oscillator”
Oscillators, harmonic see “Harmonic oscillator”
Oscillators, Rayleigh 468—479 476—478f 483p 554—556 556f 557f
Oscillators, Van der Pol 202p 483p 567p
Oscillatory behaviors see “Periodic behaviors”
Outer, approximation, in boundary-layer theory 421—484 488
Outer, limit, defined 427
Outer, region, characteristics of 420 420f 423—424
Outer, solution, in boundary-layer theory 421—484 (see also “Boundary-layer theory”)
Pade approximants 383—410
Pade approximants for 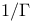 385 387t 385 387t
Pade approximants for 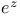 384—385 385 386t 414p 416p 384—385 385 386t 414p 416p
Pade approximants for 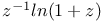 385 388 409 412p 385 388 409 412p
Pade approximants for parabolic cylinder functions 389 392
Pade approximants for Stieltjes series 387—388 390 404—410 415—416p
Pade approximants for Stirling series 388—389 391
Pade approximants, continued fractions and 396—398
Pade approximants, convergence of 400—410
Pade approximants, definition of 383—384
Pade approximants, diagonal sequence of 383
Pade approximants, distribution of zeros and poles 384—385 386t 388t 412p 416p
Pade approximants, generalized (two-point) 393—395 394f 414p
Pade approximants, generalized Shanks transformation and 389—392 412p
Pade approximants, monotonicity of 407—409
Pade approximants, normal sequence of 396—398
Pade approximants, Taylor series vs. 384—387 385—388 400
Pade summation 383—410 (see also “Pade approximants”)
Painleve transcendents, first, asymptotic behavior 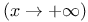 158—161 161f 162 158—161 161f 162
Painleve transcendents, first, asymptotic behavior 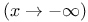 161 163—164 164f 165f 161 163—164 164f 165f
Painleve transcendents, first, numerical solutions to 198—199p
Painleve transcendents, second 199p 200p
Parabolic cylinder equation, differential equation 14 337 573
Parabolic cylinder equation, eigenvalue problem for (quantum harmonic oscillator) 28 133 332—333 522—523 538
Parabolic cylinder equation, internal boundary layers described by 456—463 482p
Parabolic cylinder equation, local analysis 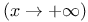 96—100 495 96—100 495
Parabolic cylinder equation, regular perturbation of 334 335 354—355 355 356—358f
Parabolic cylinder equation, second-order one-turning-point problem described by 532
Parabolic cylinder equation, singular perturbation of 334—335 337—338 353—354
Parabolic cylinder functions, asymptotic series, 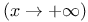 98—100 265 98—100 265
Parabolic cylinder functions, asymptotic series, 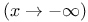 131—133 131—133
Parabolic cylinder functions, asymptotic series, 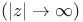 131—136 574 131—136 574
Parabolic cylinder functions, definition of 97
Parabolic cylinder functions, difference equation for 574
Parabolic cylinder functions, functional relations for 132 574
Parabolic cylinder functions, integral representations for 315p 574
Parabolic cylinder functions, leading asymptotic behaviors, 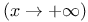 97 97
Parabolic cylinder functions, leading asymptotic behaviors, 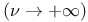 315p 315p
Parabolic cylinder functions, leading asymptotic behaviors, 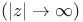 117 134—136 142—143p 117 134—136 142—143p
Parabolic cylinder functions, optimal asymptotic approximations for 98f 99—100 99f 100t 243p
Parabolic cylinder functions, Pade approximants for 389 392t
Parabolic cylinder functions, relation to Hermite polynomials 99 133 574
Parabolic cylinder functions, Stokes behavior of 117 131—133
Parabolic cylinder functions, Taylor series for 574
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



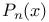 , behavior of
, behavior of 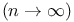
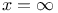
 and
and  as weight function in Stieltjes series
as weight function in Stieltjes series