Авторизация
Поиск по указателям
Rektorys K. — Survey of Applicable Mathematics.Volume 2.
Обсудите книгу на научном форуме Нашли опечатку?
Название: Survey of Applicable Mathematics.Volume 2.Автор: Rektorys K. Аннотация: This major two-volume handbook is an extensively revised, updated second edition of the highly praised Survey of Applicable Mathematics, first published in English in 1969.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2ndГод издания: 1994Количество страниц: 978Добавлена в каталог: 30.08.2014Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Space(s), energetic II 361 Space(s), Euclidean II 319 II Space(s), Hilbert II 334 II Space(s), ideal elements II 327 Space(s), isometric II 328 Space(s), linear metric II 330 Space(s), Metric II 323 Space(s), metric, linear II 330 Space(s), normed II 331 Space(s), normed, sharply II 667 Space(s), operators in see "Operator(s)" Space(s), parameter II 746 Space(s), precompact II 329 Space(s), prehilbert (pre-Hilbert) II 333 Space(s), probability II 691 Space(s), reflexive II 350 Space(s), relatively compact II 329 Space(s), self-adjoint II 350 Space(s), separable II 328 Space(s), Sobolev II 340 II Space(s), Sobolev, defined on boundary of domain II 474 Space(s), Sobolev, immersion (embedding) theorems II 343 II Space(s), Sobolev, weighted II 341 Space(s), unitary II 333 Spaethe theorem II 48 Special Cauchy problem II 150 Special functions of mathematical physics I 713 Spectral analysis (Fourier analysis) II S14 Spectral decomposition of autocovariance function II 815 Spectral decomposition of stationary process II 817 Spectral density II 815 Spectral density, estimation of II 820 Spectral density, inverse formula II 816 Spectral density, Parzen estimator of II 820 Spectral density, Tukey — Hanning estimator of II 820 Spectral distribution function II 815 Spectral radius II 604 Spectrum of matrix II 628 Spectrum of operator II 355 Spectrum of stochastic process II 815 Sphere in Euclidean space II 321 Sphere in metric space II 326 Sphere, equation of I 209 Sphere, geometrical formulae for I 109 ff Sphere, homeomorfic image of II 322 Sphere, open II 322 Sphere, sector of I 109 Sphere, segment of I 110 Sphere, volume, surface, moment of inertia I 109 ff Spherical coordinate surfaces I 197 Spherical coordinates I 196 I Spherical coordinates in solid analytic geometry I 196 Spherical coordinates, generalized I 593 Spherical coordinates, transformations, of differential equations and expressions I 432 ff Spherical coordinates, transformations, of vectors and corresponding operators I 236 Spherical functions I 705 Spherical harmonics I 708 Spherical layer I 110 Spherical Legend re functions I 705 Spherical ring I 110 Spherical surface interior diameter I 609 Spherical triangle I 82 Spherical triangle, area I 83 Spherical triangle, Euler I 82 Spherical triangle, fundamental properties I 83 Spherical triangle, general, (oblique) I 85 Spherical triangle, right-angled I 84 Spherical trigonometry I 82 ff Spheroid, prolate and oblate I 110 Spirals, Archimedes I 136 Spirals, hyperbolic or reciprocal I 138 Spirals, logarithmic, equiangular or logistic I 139 Spline(s) II 684 Spline(s), classical II 685 Spline(s), classical, cubic II 685 Spline(s), classical, natural II 686 Spline(s), Hermite II 687 Spring constant I 156 Square integrable functions I 565 II Square matrix I 50 Square nets II 549 Stability of solutions of system of ordinary differential equations II 113 Standard deviation II 701 Standard deviation, sample II 737 Standard fundamental system II 55 Standard integrals I 449 ff Standard sample II 737 Star of planes I 204 Starting point of vector I 226 Statical moment, integral calculus for, curves in space I 620 Statical moment, integral calculus for, plane curves I 618 Statical moment, integral calculus for, plane figures I 623 Statical moment, integral calculus for, solids I 627 Statical moment, integral calculus for, surfaces I 630 Stationary distribution II 800 Stationary heat conduction equation II 530 Stationary points of function I 303 Stationary process, strict and weak II 811 Stationary traffic II 806 Statistic(s) II 736 Statistic(s), estimator II 736 Statistic(s), mathematical II 735 ff Statistic(s), order II 730 Statistical model II 735 Steady state (oscillations) I 162 Step of quadrature formula I 557 Stereographic projection II 243 Stieltjes integral I 567 ff Stiff differential system II 511 Stiffness matrix II 423 Stirling formula for factorials I 550 Stirling interpolation formula II 681 Stochastic process see "Process" Stokes theorem I 614 I II Straight line(s), angle between I 174 I Straight line(s), bisectors of angle between I 177 Straight line(s), condition for being parallel or perpendicular to plane I 208 I Straight line(s), conditions for 2 to be parallel or perpendicular I 175 I Straight line(s), directed (oriented) I 174 Straight line(s), distance of a point from I 178 I Straight line(s), equation I 170 I Straight line(s), equation, directed (oriented) I 174 Straight line(s), equation, examples and theorems I 171 ff Straight line(s), equation, general, vector and parametric forms I 170 I Straight line(s), equation, gradient and intercept I 170 Straight line(s), equation, intersection of 2 lines I 172 Straight line(s), equation, normal equation I 177 Straight line(s), equation, pencil of lines I 173 Straight line(s), equation, reduced I 205 Straight line(s), equation, through 2 given points I 172 I Straight line(s), forming conic sections I 189 Stress tensor II 203 Strictly monotone operator II 372 Strong (Frechet) differential II 373 Strongly Bochner measurable abstract function II 366 Strophoid I 151 Sturges rule II 742 Sturm theorem II 47 II Sturm — Liouville problem II 83 II Subnormal I 124 I Subsequences I 339 Subset I 45 subspace II 331 Substantialy singular point I 309 Subtangent I 124 I Successive approximations in solving integral equations II 585 Successive overrelaxation metod II 619 Sum of series I 344 I Sum of series in metric space II 333 Sum of series in space I 667 Summabilities of series I 645 Summation convention (tensors) I 243 Supercritical damping I 159 Superosculating circle I 284 Supremum (l.u.b.) I 5 Surface(s) of revolution I 219 Surface(s), conical I 224 Surface(s), contravariant and covariant vector on I 252 Surface(s), cuspidal edge I 316 Surface(s), definition I 209 I Surface(s), differential calculus, application to I 628 Surface(s), discriminant I 324 Surface(s), edge of regrassion I 316 Surface(s), element of area I 324 Surface(s), elliptic point of I 325 Surface(s), envelope of one-parameter family I 318 Surface(s), equipotential I 233 Surface(s), explicit equation of I 306 Surface(s), finite piecewise smooth I 305 Surface(s), first fundamental form I 253 I Surface(s), fundamental coefficients I 324 Surface(s), Gaussian curvature I 330 Surface(s), generator of I 317 I Surface(s), hyperbolic point of I 325 Surface(s), integrals I 009 ff Surface(s), integrals, of first and second kinds I 610—611 Surface(s), interior diameter I 609 Surface(s), lines of curvature I 331 Surface(s), mean curvature I 330 Surface(s), non-developable I 316 Surface(s), normal curvature I 328 Surface(s), normal section radius of curvature I 328 Surface(s), oriented I 609 Surface(s), orthogonal conjugate net on I 331 Surface(s), parabolic point of I 325 Surface(s), parameters and parametric equations I 306 Surface(s), regular points on I 209 I Surface(s), ruled I 221 Surface(s), scalar on I 252 Surface(s), scroll (skew surface) I 316 Surface(s), second fundamental form I 325 Surface(s), second order I 209 ff Surface(s), shape with respect to tangent plane I 325 Surface(s), simple finite piecewise smooth I 575 Surface(s), singular point on I 209 I Surface(s), tensor on I 251 Surjective operator (mapping) II 344 Sylvester law of inertia I 67 Symbols O(g(x)), o(g(x)) I 376 Symmetric eigenvalue problem II 82 Symmetric kernels of integral equations II 231 Symmetric matrices I 51 Symmetric operators II 359 Symmetric problems II 82 System(s), closed in Hilbert space II 337 System(s), closed in Hilbert space, in space I 675 System(s), complete in Hilbert space II 337 System(s), complete in Hilbert space, in space I 675 System(s), of decompositions II 447 System(s), of decompositions, regular II 447 System(s), of ordinary differential equations II 2 II II System(s), of partial differential equations II 149 II System(s), orthogonal in Hilbert space II 336 System(s), orthogonal in Hilbert space, in space I 670 System(s), orthonormal in Hilbert space II 336 System(s), orthonormal in Hilbert space, in space I 670 T-scheme I 557 II t-test II 757 ff Table of analysis of variance II 782 Table of Bessel functions I 695 I Table of boundary value problems II 411 Table of Fourier transforms II 582 II Table of integrals I 470—511 I Table of Laplace transforms II 578 II Table of Legend re polynomials I 707 Table of solved differential equations II 120 ff Table of zeros of I 695 Table, contingency II 763 Table, correlation II 741 Table, frequency II 741 Tabular points II 675 Tangent and cotangent, integrals containing them I 501 ff Tangent(s) to conic I 191 ff Tangent(s), developable (surface) I 316 Tangent(s), direction, angle and length, in polar coordinates I 300 Tangent(s), drawn to curve from arbitrary point I 303 Tangent(s), length, in polar coordinates I 301 Tangent(s), plane of surface I 311 Tangent(s), plane to curve I 272 Tangent(s), surface I 316 Tangent(s), theorem I 79 Tangent(s), vector field I 249 Tangent(s), vector to curve I 232 I Tangential vector to surface I 311 Taylor expansion for functions of one complex variable II 264 Taylor expansion for functions of several complex variables II 285 Taylor expansion method II 491 Taylor formula I 396 Taylor formula for polynomials I 23 Taylor series I 652 II Taylor theorem I 396 I Taylor theorem for several variables I 414 Temperature distribution, examples using, finite difference method II 559 Temperature distribution, examples using, Fourier method II 539 ff Temperature distribution, examples using, Laplace transform II 571 II Tensor(s), alternating I 256 Tensor(s), calculus I 242 ff Tensor(s), characteristic numbers of I 258 Tensor(s), conjugate directions I 257 Tensor(s), contravariant and covariant I 247 Tensor(s), contravariant and covariant, on surface I 249 Tensor(s), deformation I 249 I Tensor(s), first fundamental of surface I 252 Tensor(s), in space I 246 ff Tensor(s), indicatrix of point I 257 Tensor(s), indices, lowering and raising of I 255 Tensor(s), metric, of space I 247 Tensor(s), metric, of surface I 252 Tensor(s), metric, on surface I 251 Tensor(s), quadratic I 247 Tensor(s), second fundamental of surface I 253 Tensor(s), symmetric and skew-symmetric I 255 Tensor(s), symmetric quadratic I 254 Term-by-term, differentiation I 644 II Term-by-term, integration I 643 II II Termination criterion for iterative methods II 616 Test(s) of linearity II 775 Test(s) of significance in normal linear regression model II 773 ff Test(s) of size II 756 Test(s), chi-square II 761 Test(s), Fisher, of periodicity II 819 Test(s), function II 82 Test(s), goodness of fit II 760 Test(s), hypothesis II 755 Test(s), Kolmogorov — Smirnov II 763 Test(s), one-sample II 757 Test(s), one-sided and two-sided II 756 Test(s), paired II 759 ff Test(s), parametric and non-parametric II 755 Test(s), t II 757 ff Test(s), two-sample II 757 ff Test(s), uniformly most powerfull II 756 Theorem(s) on continuous extension of functional and operator II 340 Theorem(s) on convergence, of finite difference method II 565 II Theorem(s) on convergence, of finite element method II 447 Theorem(s) on eigenvalues, of differential equations II 84 Theorem(s) on eigenvalues, of operators II 355 II II Theorem(s) on existence and uniqueness of solution of problems, in ordinary differential equations II 5 II II Theorem(s) on existence and uniqueness of solution of problems, in partial differential equations II 177 II II II II II Theorem(s) on Fredholm integral equations II 225
Реклама
 |
|
О проекте
|
|
О проекте



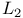
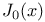 ,
, 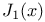 ,
, 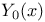 ,
,