|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cox D., Katz S. — Mirror symmetry and algebraic geometry |
|
|
 |
| Предметный указатель |
Reflexive polytope for quintic mirror 61
Reflexive polytope, Batyrev duality for 46 56
Reflexive polytope, classification of 47
Reflexive polytope, definition of 46
Reflexive polytope, example of 49 51 71 88 124 125 139 146
Reflexive sheaf 37
Regular singular point 20 75 77 246 247
Regular triangulation 43 44
Regularity lemma see “Mirror theorems Givental regularity
Reid’s fantasy 143 405
Renormalization 2 7 8 423
Residue map 83 86
Residue matrix  77 79 246 77 79 246
Ricci curvature tensor 10
Riemann — Roch theorem 289 294 295
Right-moving, fermions 2 421
Right-moving, sector 425
Satake — Baily — Borel compactification 132
Schrodinger picture 413
Secondary fan 43 117 120 121 135 136 142 143 148 155 156 decomposition”)
Secondary fan, enlarged 430
Secondary fan, example of 50 51 124 126 140
Secondary polytope 120
Seiberg — Witten curve 406
Semi-ample 54
Semi-positive 185 187 189 210
Serre — Grothendieck duality 55
Seven variety 198
Sigma model 3 4 6 7 9—11 15 168 302 334 419—423 428—430
Sigma model, A-model 421
Sigma model, action of see “Action of
Sigma model, B-model 421
Sigma model, fermionic fields of 419 421 425
Sigma model, supersymmetric 421 423
Sigma model, topological 434
Sigma model, twisted 421 422
Singularity 407—410
Singularity,  -factorial 11 55 407 -factorial 11 55 407
Singularity, canonical 11 12 407 408
Singularity, Cohen — Macaulay 407
Singularity, Gorenstein 11 12 55 116 407
Singularity, terminal 11 54 55 116 407 408 410
Singularity, toroidal 410
Small subgroup 408
Sparse resultant 122
Spin bundle 419
Spin geometry 426
Spinors 426
Stable 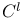 map 188 191 map 188 191
Stable 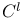 map, equivalence of 188 map, equivalence of 188
Stable maps, automorphisms of 281 283 284 290—292 340 341 368 370 377
Stable maps, definition of 169
Stable maps, family of 169
Stable maps, graph construction 319 334
Stable maps, moduli of 16 27 173 and
Stable maps, moduli of, dimension of 170
Stable maps, moduli of, expected dimension of 171 175 180 187 192 211 306 308
Stable maps, moduli of, stack 170 175 180 181 301 302 357—359 364
Stable maps, moduli of, tangent space of 175 285 290
Stable maps, moduli ofcoarse 169 170 178 181 301
Stable maps, universal 179 301 302 305
STACK see “Algebraic stack”
Stanley — Reisner ideal 223 224
Stanley — Reisner ideal, quantum 224 225 392
Stationary phase method 417 422
String theory 1 2 7 419
String theory, limit of 406
String theory, periods of 406
Suborbifold 55 409
Supercommutative 219 221 229 230 233 234 240 434
Superconformal, field theory (SCFT) 2 4 6 7 9 10 12 17 53 56
Superconformal, N = 2 algebra 2
Superconformal, N = 2 representation 56
Superfield 426 427 429
Superfield, chirai see “Chiral superfield”
Supergravity 10
Supermanifold 229 230 239 426
Supermanifold, partial derivatives on 229 304
Supermanifold, tangent bundle of 240
Superpotential 426 428 430
Superpotential, quintic 429
Superstring theory, duality of 404
Superstring theory, heterotic 2 3 404 420 421
Superstring theory, type I 2
Superstring theory, type II 2 145 404
Supersymmetric field theory 406 420 426
Supersymmetry l—3 7 10 424—426 supersymmetric”)
Supersymmetry, N = 2 algebra 426
Supersymmetry, transformation 2 420 422 426
Supervector space 431 434
Support function 32
Support function, upper convex 33
Support function, upper convex, strictly 33 35
Support of a fan see “Fan support
Symplectic action 40
Symplectic manifold 40 184 185 209 228
Symplectic manifold, semi-positive see “Semi-positive”
Symplectic orbifold 42 410
Symplectic quotient see “Symplectic reduction”
Symplectic reduction 41 42 44 45 143 410
T-duality 402 403
Tangent functor 176
Tangent weight see “Weights of a representation tangent”
Tangent-obstruction complex 176 178—180 285
Tangent-obstruction complex for virtual fundamental class 178
Tangent-obstruction complex, perfect 174 181
Tangent-obstruction complex, perfect, definition of 176
Tangent-obstruction complex, perfect, example of 177
Three-point function see “Correlation function three-point”
Time-ordered product 417
| Toda lattice 228
Topological quantum field theory 167 168 217 416 422 430—435
Topological quantum field theory, (0 + 1)-dimensional 431 432
Topological quantum field theory, (2 + l)-dimensional 435
Topological quantum field theory, (d + l)-dimensional 431
Topological quantum field theory, (l + 1)-dimensional 432
Topological quantum field theory, (l + 1)-dimensional, gives Frobenius algebra 432 434
Topological quantum field theory, definition of 431
Topological quantum field theory, relation to A-model 434
Topological recursion relation 311 312
Topological sigma model 167
Topological sigma model, coupled to gravity 167 187
Toric complete intersection 6 62
Toric complete intersection, Calabi — Yau 6 62 382 430
Toric complete intersection, nef 96 97 128 381 382 389
Toric Mirror theorem see “Mirror theorems Givental toric”
Toric part of cohomology 134 143 156 158 267 361 382
Toric part of cohomology, definition of 57 271
Toric variety 32 382 407
Toric variety, affine 32 129
Toric variety, automorphism group 47 48 58 61 62 116—118 125
Toric variety, automorphism group, dimension of 48
Toric variety, automorphism group, roots 48 124 126
Toric variety, Batyrev quantum ring of see “Batyrev quantum ring”
Toric variety, Chow group of 32 36
Toric variety, cohomology ring of 223 392
Toric variety, complete 32
Toric variety, divisors on 33
Toric variety, examples of 49—52
Toric variety, Fano 46 47 49 51 53 389—393 395
Toric variety, homogeneous coordinate ring of 36 47—50 85 92 117 125 430
Toric variety, ideal-variety correspondence 38
Toric variety, Kahler cone of 38 39 41 392 393 429
Toric variety, Mori cone of 39 40 383 389 393
Toric variety, Picard group of 32 224
Toric variety, quantum cohomology of see “Quantum cohomology small of
Toric variety, simplicial 32 37 38 41 47 48 408
Toric variety, smooth 32 381
Toric variety, via fans see “Fan toric
Toric variety, via homogeneous coordinates 37
Toric variety, via polytopes see “Polytope toric
Toric variety, via symplectic reduction 41 42 45 430
TQFT see “Topological quantum field theory”
TRR see “Topological recursion relation”
Tube domain 130
V-manifold 408 (see also “Orbifold”)
Vacuum state 415 417 425 427
Vafa — Intriligator formula 227
Vanishing cycle 19
Vector superfield 428
Verlinde algebra 227
Virasoro algebra 310 311 423—425
Virasoro algebra, central extension of 310 425
Virasoro conjecture 310 425
Virasoro conjecture, consequences for gravitational descendents 311
Virasoro conjecture, consequences for Gromov — Witten invariants 310 311
Virasoro constraints 211
Virtual fundamental class 16 172 174—183 191 207 288 294 299 302 305 306 308 313 358 360 381
Virtual fundamental class for a complete intersection 386 400
Virtual fundamental class for a complete intersection in 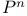 360 360
Virtual fundamental class for Calabi — Yau threefold 288 289
Virtual fundamental class for Fermat quintic 174
Virtual fundamental class for quintic threefold 173 180 181 360
Virtual fundamental class, compatibility with forgetful map 182 305
Virtual fundamental class, compute using Euler class 182 208 211 289 308 309
Virtual fundamental class, definition of see “Obstruction theory and tangent-obstruction complex”
Virtual fundamental class, definition of, Behrend — Fantechi approach 178 179
Virtual fundamental class, definition of, Behrend — Fantechi definition 179
Virtual fundamental class, definition of, equivalence of definitions 176 195 399
Virtual fundamental class, definition of, Li — Tian approach 176—178 181
Virtual fundamental class, definition of, Li — Tian definition 177 178
Virtual fundamental class, degree is expected dimension 178 192 222 304
Virtual fundamental class, equivariant 299 300 382
Virtual fundamental class, equivariant, localization formula for 285 300 382
Virtual fundamental class, example of 177 179
Virtual fundamental class, properties of 180—183 195 304
Virtual fundamental class, relative 180
Virtual neighborhood 188
Virtual normal bundle 282 300
Virtual normal cone see “Normal cone virtual”
Virtual tangent space 300
WDW equation see “Dubrovin connection and Gromov — Witten potential”
Weighted homogeneous polynomial 426 427
Weighted projective space 6 49 50 53 70 71 140
Weighted projective space, criterion to be Fano 47 50
Weights of a representation 276 278 280 285 292 344 369 370
Weights of a representation of normal bundle 285 289
Weights of a representation, obstruction 289—292 297
Weights of a representation, tangent 278 281 285 287 290 297
Weights of variables 358 365 378 379
Witten conjecture 310
World sheet 1 2 10 419 422—427
World sheet, non-perturbative corrections 7
Worldvolume 402
Yang — Mills theory 417
Yukawa coupling 7—10 416 421
Yukawa coupling of a Calabi — Yau threefold 102—112 256 259 327
Yukawa coupling of a Calabi — Yau threefold, 1-dimensional moduli 102 105—107
Yukawa coupling of a Calabi — Yau threefold, 2-dimensional moduli 102—104
Yukawa coupling of a Calabi — Yau threefold, r-dimensional moduli 107—109
Yukawa coupling, differs from normalized coupling 268
Yukawa coupling, normalized 104—112 257 259 268 386
Yukawa coupling, normalized in terms of periods 389 399
Yukawa coupling, normalized of the quintic mirror see “Quintic mirror Yukawa
Yukawa coupling, normalized, definition of 110
Yukawa coupling, normalized, minus sign 8 21 107
Yukawa coupling, normalized, relation to mirror map 109—112 151
Yukawa coupling, normalized, relation to the Gauss — Manin connection 105 108
Yukawa coupling, toric 268 269 385 B-model toric”)
Zariski p-form 409
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




 -factorial
-factorial 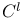 map
map