|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cox D., Katz S. Ч Mirror symmetry and algebraic geometry |
|
|
 |
| ѕредметный указатель |
Dubrovin connection, flatness of 240 244
Dubrovin connection, formal 242
Dubrovin connection, homogeneity of 241
Dubrovin connection, potential function of 239
Dubrovin connection, torsion of 240
Dubrovin connection, WDVV equation for 240 241
Dubrovin formalism 234 239Ч242 244 304
Dubrovin formalism, binary product of 239
Dubrovin formalism, connection of see УDubrovin connectionФ
Electromagnetic potential 417
Energy-momentum conservation 424
Energy-momentum tensor 424
Enumerative geometry 16 215 enumerative
Equivariant characteristic class 338
Equivariant Chern class 276 280 366
Equivariant cohomology 27 101
Equivariant cohomology of 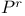 277 278 335 277 278 335
Equivariant cohomology, definition of 276
Equivariant cohomology, explanation of parameter h 319
Equivariant cohomology, localization of 277 336 for
Equivariant cohomology, restriction map 343 344
Equivariant hyperplane class 28 101 335 346 366 368
Equivariant hyperplane class of  see У see У projective equivariant projective equivariant
Equivariant hyperplane class, definition of 277
Equivariant integral 280 335 367 368 373 376 377
Equivariant integral, definition of 279
Equivariant vector bundle 276 298
Euler  -function 162 163 165 -function 162 163 165
Euler characteristic 310
Euler class 173 289 351 358 360
Euler class of zero bundle 358 365 372
Euler class, equivariant 276 292 336 338 341 342 344 377
Euler class, equivariant of 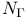 285 287Ч289 291 293 370 285 287Ч289 291 293 370
Euler class, stack versus coarse moduli space 181 184 302 332 337
Euler data 27 28 345 348Ч350 380
Euler data, definition of 339
Euler data, examples of see УP and QФ
Euler data, hypergeometric function of 346 (see also УHG of
Euler data, linked 343 345 353 355
Euler data, linked, definition of 342
Euler data, linked, mirror transformation of 348 352 353 381 mirror
Euler data, linked, multiple cover interpretation 343
Euler data, linked, uniqueness theorem for 344 348 353 355 380
Euler integral 160 (see also УGKZ systemФ)
Euler Ч Lagrange equation 412Ч414 418 421 422 424
Euler Ч Lagrange equation for electricity and magnetism 417
EulerТs constant 162
Evaluation map 172 179 189 205 210 222 298 301 332 357 360 365 375
Excess dimension 308
Excess dimension for moduli of stable maps 182
Excess dimension in intersection theory 182
Excess normal bundle 173 174
Expected dimension in Kuranishi theory 174
Expected dimension of moduli of stable maps see УStable maps moduli
Expected dimension of zero locus 173
Extremal transition 143 144 146 405 406
Extremal transition, compatibility with mirror symmetry 144 148
Extremal transition, dual 147 148 158 159 405
Extremal transition, example of 146Ч148 158
Extremal transition, mirror see УExtremal transition dualФ
Extremal transition, relation to SCFT moduli 144
Extremal transition, toric 145
Extremal transition, Type I 143 145
Extremal transition, Type II 143
Extremal transition, Type III 143 145
F-theory 404
Face of a cone 31
Fan 31 (see also УProjective subdivisionФ)
Fan, complete 32
Fan, flip of see УFlipФ
Fan, Grobner see УGrobner fanФ
Fan, secondary see УSecondary fanФ
Fan, simplicial 32
Fan, smooth 32
Fan, support of 31
Fan, supported on a linear circuit see УLinear circuit supported
Fan, symmetries of 48
Fan, toric variety of 32 51
Fano variety 46 218 219 223 228 405
Fermion 2 419Ч421 425
Fermion, relation to supercommuting variables 230 419
Fermionic field 419 420 fermionic
Fermionic variables 419 427 428
Feynman diagram 196
Feynman integral 2 7
Field strength 417 418
Field, bosonic see УBosonic fieldФ
Field, classical 411 414 416
Field, fermionic see УFermionic fieldФ
Field, primary 424
Field, quantum 414 416
Field, theory 411 414
Flag manifold 219 228 254
Flag manifold, complete intersection in 364 366
Flag manifold, complete intersection in, Calabi Ч Yau 405
Flag of graph  285 (see also УLocalization in 285 (see also УLocalization in  d)$"/> fixed d)$"/> fixed
Flip 137 139
Flip, example of 141
Flip, geometric significance of 137 (see also УFlop generalizedФ)
Flip, trivial 137 138 141 142 156
FLOP 43 133 147 225 226
Flop, example of 141
Flop, generalized 137
Flop, trivial 137
Fourier transform 414 418
Frobenius algebra 221 234 240 430 435
Frobenius algebra, definition of 432
Frobenius algebra, gives (l + 1)-dimensional TQFT 432 434
Frobenius algebra, n-point function of 432 434
Frobenius algebra, three-point function of 432
Frobenius algebra, trace map of 432
Frobenius manifold 241
Frobenius method 26 77 161Ч163 333
Frobenius method in cohomology ring of 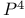 164 164
Frobenius method, example of 162 165
Fundamental class 172
Gale transform 44
Gauge choice 418 419 424
Gauge fixing 417
Gauge group 417 419 420 424 429
Gauge group for electricity and magnetism 418
Gauge theory 417 428
Gauged linear sigma model 12 42 45 334 428Ч430
Gauged linear sigma model, action of 428
Gauged linear sigma model, action of, bosonic part of 428
Gauged linear sigma model, correlation function of 364
Gauged linear sigma model, example of 429
Gauged linear sigma model, gauge group of 428
Gauged linear sigma model, mirror symmetry for 430
Gauged linear sigma model, phases of 143 (see also УPhasesФ)
Gauged linear sigma model, phases of Calabi Ч Yau 429
Gauged linear sigma model, phases of Landau Ч Ginzburg 430
Gauged linear sigma model, relation to toric geometry 429
Gauss Ч Manin connection 8 25 75 82 151 250 259 265Ч267
Gauss Ч Manin connection of a Calabi Ч Yau threefold 106 108 109 251 257 258
Gauss Ч Manin connection, connection matrix see УConnection matrixФ
Gauss Ч Manin connection, definition of 74
Gauss Ч Manin connection, fiat integral section 82 106 111 150 151 387
Gauss Ч Manin connection, relation to normalized Yukawa coupling 105
Generalized Berglund-Hiibsch transposition rule 70
Generalized fiop see УFlop generalizedФ
Generalized Fredholm orbifold bundle 191
Generalized Fredholm orbifold bundle, oriented Euler class of 191
generated by global sections 33
Genus g coupling 303 312
Genus g gravitational Gromov Ч Witten potential 303
Genus g gravitational Gromov Ч Witten potential, definition of 304
Geometric quotient 37 117
Geometrically engineered theory 406
Ghosts 424
| GIT quotient 117 120 122
Giventai connection 316
Giventai connection, definition of 311
Giventai connection, dual 321 329
Giventai connection, flat sections of 311Ч313 319
Giventai connection, flat sections of, restriction of 314 322
Giventai connection, flat sections of, symbolic notation for 312
Giventai connection, relation to Dubrovin connection 245
Giventai connection, restriction to 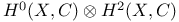 314 320 314 320
Giventai connection, restriction to H^2(V,\mathbb{C}) 315
Giventai I-function for  393 394 393 394
Giventai I-function for  357 357
Giventai I-function for  357 365 371 357 365 371
Giventai I-function for a toric variety 389
Giventai I-function when  is nef 393 is nef 393
Giventai I-function,  26 27 100 358 379 380 26 27 100 358 379 380
Giventai I-function,  for a convex variety 381 for a convex variety 381
Giventai I-function,  for a toric variety 381 383 for a toric variety 381 383
Giventai I-function,  for hypersurface in P(1,1,2,2,2) 384 for hypersurface in P(1,1,2,2,2) 384
Giventai I-function,  for quintic threefold 26 98 101 164 361 362 for quintic threefold 26 98 101 164 361 362
Giventai I-function,  , definition of 356 , definition of 356
Giventai I-function,  , example of 364 , example of 364
Giventai I-function,  , satisfies Picard Ч Fuchs equations of mirror 101 121 128 383 385 399 , satisfies Picard Ч Fuchs equations of mirror 101 121 128 383 385 399
Giventai I-function, 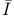 98Ч101 128 164 359 98Ч101 128 164 359
Giventai I-function, 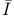 , satisfies A-system 98 391 , satisfies A-system 98 391
Giventai I-function,  365 366 365 366
Giventai I-function, equivariant version of  371 371
Giventai I-function, equivariant version of  379 382 379 382
Giventai J-function 25 320Ч325 358 359
Giventai J-function for 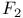 393 394 393 394
Giventai J-function for  324 357 324 357
Giventai J-function for  324 325 346 357 365 324 325 346 357 365
Giventai J-function for a Calabi Ч Yau threefold 325Ч329
Giventai J-function for a Calabi Ч Yau threefold, formula for 325 326
Giventai J-function for a Calabi Ч Yau threefold, in terms of Gromov Ч Witten potential 326
Giventai J-function for a Calabi Ч Yau threefold, second partials of 326 363
Giventai J-function for a toric variety 389
Giventai J-function for a toric variety, when  is nef 393 is nef 393
Giventai J-function for hypersurface in P(1,1,2,2,2) 386 388
Giventai J-function for quintic threefold 25 362
Giventai J-function,  26 358 359 379 380 26 358 359 379 380
Giventai J-function,  for a convex variety 365 for a convex variety 365
Giventai J-function,  for a toric variety 381Ч383 for a toric variety 381Ч383
Giventai J-function,  for hypersurface in P(l,1,2,2,2) 384 388 for hypersurface in P(l,1,2,2,2) 384 388
Giventai J-function,  for quintic threefold 26 362 for quintic threefold 26 362
Giventai J-function,  , definition of 358 , definition of 358
Giventai J-function,  , example of 364 , example of 364
Giventai J-function,  , gives relations in modified quantum cohomology 363 , gives relations in modified quantum cohomology 363
Giventai J-function,  , gives relations in quantum cohomology 364 , gives relations in quantum cohomology 364
Giventai J-function,  , symbolic notation for 358 , symbolic notation for 358
Giventai J-function, definition of 320
Giventai J-function, equivariant version of  366 366
Giventai J-function, equivariant version of  , definition of , definition of 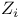 367 367
Giventai J-function, equivariant version of  , definition of S 366 , definition of S 366
Giventai J-function, equivariant version of  372 382 372 382
Giventai J-function, equivariant version of  , definition of , definition of 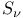 372 373 372 373
Giventai J-function, equivariant version of  , definition of $Z_{i,\nu} 373 , definition of $Z_{i,\nu} 373
Giventai J-function, equivariant version of  , definition of , definition of 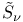 372 373 372 373
Giventai J-function, formulas for 322 356
Giventai J-function, gives relations in quantum cohomology 321
Giventai J-function, primitive part of 361
Giventai J-function, relation between 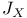 and and  359 360 382 386 400 359 360 382 386 400
Giventai J-function, symbolic notation for 322 356 360
Giventai J-function, toric part of 382
GKZ decomposition 43 44 60 120 121 139 143 155 161 225 430
GKZ decomposition, enlarged 43 430
GKZ decomposition, examples of 50Ч52 124 127 140
GKZ system 95 96 100 101 122Ч123 125 158Ч166 333 383
global sections of 34?
GLSM see УGauged linear sigma modelФ
Gluing lemma 338 342 380
Grassmannian 167 173 219 227 228 281 293 405
Grassmannian, Caiabi Ч Yau complete intersection in 405
Grassmannian, Caiabi Ч Yau complete intersection in threefold 366
Gravitational class 306 309
Gravitational class, definition of 305
Gravitational correlators 25 196 211 301Ч311 320 382 383
Gravitational correlators, axioms for see УGravitational classФ
Gravitational correlators, axioms for Degree Axiom 304 310 311 317 318 325 360
Gravitational correlators, axioms for Dilaton Axiom 306Ч308 310 318
Gravitational correlators, axioms for Divisor Axiom 305Ч308 310 314 318 357
Gravitational correlators, axioms for Fundamental Class Axiom 305Ч308 318 324 325
Gravitational correlators, axioms for Splitting Axiom 305Ч307 313
Gravitational correlators, coefficients 303
Gravitational correlators, definition of 302
Gravitational correlators, genus 0 correlators in terms of Gromov Ч Witten invariants 306
Gravitational correlators, genus 0 correlators of 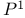 306 357 306 357
Gravitational correlators, genus 0 correlators of 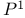 , recursion for 307 308 , recursion for 307 308
Gravitational correlators, genus 0 correlators of Calabi Ч Yau threefolds 308
Gravitational correlators, genus 1 correlator  308 309 308 309
Gravitational correlators, genus 1 correlator  , relation to Euler characteristic 310 , relation to Euler characteristic 310
Gravitational correlators, recursions coming from TRRs 311 (see also УTopological recursion relationФ)
Gravitational correlators, relation to Gromov Ч Witten invariants 303
Gravitational correlators, symbolic notation for 315 356
Gravitational descendants 302 311
Gravitational descendants, relation to gravitational correlators 303
Gravitational Gromov Ч Witten potential see УGenus g gravitational Gromov Ч Witten potentialФ
Gravitational potential 310
Gravitational quantum product 234 304
Gravitational quantum product, coefficients 304
Griffiths transvereality 74 76 102 103 111 252 254
Griffiths transvereality for projective hypersurfaces 83
Griffiths transvereality for the A-variation of Hodge structure see УA-variation of Hodge structure Griffiths
Griffiths Ч Dwork method 83Ч87 94 96
Griffiths Ч Dwork method for projective hypersurfaces 83Ч85
Griffiths Ч Dwork method for toric hypersurfaces 85-87
Griffiths Ч Dwork method for toric hypersurfaces, limitations of 86
Griffiths Ч Dwork method for weighted projective hypersurfaces 85
Griffiths Ч Dwork method, description of 84
Griffiths Ч Dwork method, examples of 87Ч90
Grobner basis techniques 84 86Ч88 90 225
Grobner fan 121 225
Gromov Ч Uhlenbeck compactification 187 209
Gromov Ч Witten class 200 212 220 232 305 309
Gromov Ч Witten class of 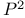 198 199 198 199
Gromov Ч Witten class, axioms for 191Ч195 304
Gromov Ч Witten class, axioms for Composition Law 194
Gromov Ч Witten class, axioms for Deformation Axiom 194 395
Gromov Ч Witten class, axioms for Degree Axiom 192 198 201 265
Gromov Ч Witten class, axioms for Divisor Axiom 193 198 200Ч203 212 235 236 239 246 265 307
Gromov Ч Witten class, axioms for Effectivity Axiom 192 228
Gromov Ч Witten class, axioms for Equivariance Axiom 192 199 201 219Ч221 233 241
Gromov Ч Witten class, axioms for Fundamental Class Axiom 193 198 199 201 212 219 234 235 265
Gromov Ч Witten class, axioms for Linearity Axiom 192
Gromov Ч Witten class, axioms for Motivic Axiom 194
Gromov Ч Witten class, axioms for Point Mapping Axiom 193 197 200 201 204 211 219 231 234 235 239 307 310 314
Gromov Ч Witten class, axioms for Reduction Axiom 194 212 310
Gromov Ч Witten class, axioms for Splitting Axiom 194 196 198 199 219 220 233 241
Gromov Ч Witten class, definition in simplest case 171
Gromov Ч Witten class, definition of 183 (see also УGromov Ч Witten invariant algebraic
Gromov Ч Witten class, intuitive definition of 168
Gromov Ч Witten class, role of fundamental class 172
Gromov Ч Witten class, symplectic 190
Gromov Ч Witten class, tree-level 196
Gromov Ч Witten invariant 7 9 15 16 24 25 28 265 266 273 281 298Ч301 307
Gromov Ч Witten invariant algebraic definition in general case 183
Gromov Ч Witten invariant algebraic definition in simplest case 171
Gromov Ч Witten invariant, algebraic definition 168Ч184 (see also УVirtual fundamental classФ)
Gromov Ч Witten invariant, algebraic definition, intuitive idea of 168
Gromov Ч Witten invariant, algebraic definition, role of fundamental class 172
Gromov Ч Witten invariant, arises in physics 422
Gromov Ч Witten invariant, axioms for 192 193 axioms
Gromov Ч Witten invariant, computing 196Ч215
Gromov Ч Witten invariant, computing elliptic invariants of 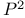 210Ч212 310 210Ч212 310
Gromov Ч Witten invariant, computing elliptic invariants of 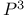 213 213
Gromov Ч Witten invariant, computing elliptic invariants of the quintic threefold 213 214
Gromov Ч Witten invariant, computing genus 0 invariants of 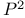 197Ч201 236 237 310 197Ч201 236 237 310
Gromov Ч Witten invariant, computing genus 0 invariants of Calabi Ч Yau threefolds 201Ч210 308 325
Gromov Ч Witten invariant, computing genus 0 invariants of the quintic threefold 184 201Ч203 Gromov
Gromov Ч Witten invariant, computing genus 2 invariants of 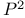 311 311
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



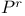

 -function
-function 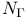

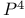
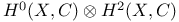



 is nef
is nef 




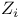
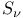
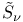
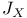 and
and