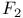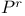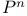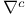|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cox D., Katz S. Ч Mirror symmetry and algebraic geometry |
|
|
 |
| ѕредметный указатель |
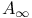 -category 403 -category 403
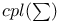 41Ч45 135Ч137 139 161 41Ч45 135Ч137 139 161
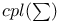 , , 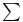 -convex 43 -convex 43
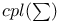 , definition in , definition in 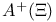 43 43
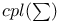 , definition in , definition in 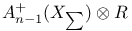 39 39
 see УGivental I-function see УGivental I-function
 see УGivental J-function see УGivental J-function
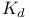 333 350 Gromov 333 350 Gromov
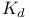 for a critical bundle 352 for a critical bundle 352
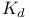 in multiple cover case 352 355 in multiple cover case 352 355
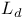 336 375 336 375
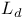 , fixed point loci 376 , fixed point loci 376
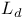 , fixed point loci, normal bundle of 377 , fixed point loci, normal bundle of 377
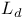 , map ft to , map ft to  375 375
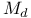 334 334
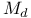 , fixed point loci 334 339 , fixed point loci 334 339
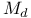 , fixed point loci, description of 334 , fixed point loci, description of 334
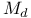 , fixed point loci, graph , fixed point loci, graph  339 339
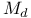 , fixed point loci, normal bundle of 341 , fixed point loci, normal bundle of 341
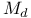 , map , map  to to  336 337 339Ч341 344 375 336 337 339Ч341 344 375
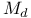 , torus action on 334 , torus action on 334
 , Gromov Ч Witten invariant for , Gromov Ч Witten invariant for 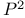 198 198
 , Gromov Ч Witten invariant for the quintic threefold 201 , Gromov Ч Witten invariant for the quintic threefold 201
 , projective space 334 375 , projective space 334 375
 , projective space, equivariant cohomology of 335 , projective space, equivariant cohomology of 335
 , projective space, equivariant hyperplane class of 335 , projective space, equivariant hyperplane class of 335
 , projective space, fixed points of 335 340 , projective space, fixed points of 335 340
 , projective space, torus action on 335 , projective space, torus action on 335
 , projective space, weights of 335 , projective space, weights of 335
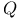 27 28 340 343 344 347 348 350 351 353 27 28 340 343 344 347 348 350 351 353
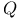 for a concavex bundle 349 for a concavex bundle 349
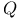 in multiple cover case 352 355 in multiple cover case 352 355
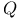 is Euler data 339 is Euler data 339
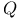 , definition of 337 , definition of 337
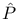 27 28 101 164 343 346 353 27 28 101 164 343 346 353
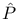 for a concavex bundle 350 for a concavex bundle 350
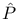 in multiple cover case 355 in multiple cover case 355
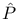 is Euler data 339 is Euler data 339
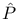 , definition of 337 , definition of 337
 and its toric blow-up 49 89 and its toric blow-up 49 89
 and its toric blow-up, Calabi Ч Yau hypersurface in 427 and its toric blow-up, Calabi Ч Yau hypersurface in 427
 and its toric blow-up, Calabi Ч Yau hypersurface in A-model correlation function of 269 386 388 and its toric blow-up, Calabi Ч Yau hypersurface in A-model correlation function of 269 386 388
 and its toric blow-up, Calabi Ч Yau hypersurface in Givental function and its toric blow-up, Calabi Ч Yau hypersurface in Givental function  384 384
 and its toric blow-up, Calabi Ч Yau hypersurface in Givental function and its toric blow-up, Calabi Ч Yau hypersurface in Givental function  386 388 386 388
 and its toric blow-up, Calabi Ч Yau hypersurface in Gromov Ч Witten potential of 387 388 and its toric blow-up, Calabi Ч Yau hypersurface in Gromov Ч Witten potential of 387 388
 and its toric blow-up, Calabi Ч Yau hypersurface in Hodge numbers of 146 and its toric blow-up, Calabi Ч Yau hypersurface in Hodge numbers of 146
 and its toric blow-up, Calabi Ч Yau hypersurface in instanton numbers of 269 270 and its toric blow-up, Calabi Ч Yau hypersurface in instanton numbers of 269 270
 and its toric blow-up, Calabi Ч Yau hypersurface in Kahler cone of 146 269 383 and its toric blow-up, Calabi Ч Yau hypersurface in Kahler cone of 146 269 383
 and its toric blow-up, Calabi Ч Yau hypersurface in Kahler moduli of 146 147 and its toric blow-up, Calabi Ч Yau hypersurface in Kahler moduli of 146 147
 and its toric blow-up, Calabi Ч Yau hypersurface in mirror map of 158 159 164Ч166 270 385 388 and its toric blow-up, Calabi Ч Yau hypersurface in mirror map of 158 159 164Ч166 270 385 388
 and its toric blow-up, Calabi Ч Yau hypersurface in Mirror Theorem for 383; 386 388 and its toric blow-up, Calabi Ч Yau hypersurface in Mirror Theorem for 383; 386 388
 and its toric blow-up, Calabi Ч Yau hypersurface in moduli coordinates of 269 and its toric blow-up, Calabi Ч Yau hypersurface in moduli coordinates of 269
 and its toric blow-up, Calabi Ч Yau hypersurface in SCFT moduli of 147 and its toric blow-up, Calabi Ч Yau hypersurface in SCFT moduli of 147
 and its toric blow-up, Calabi Ч Yau hypersurface in toric Kahler cone of 148 and its toric blow-up, Calabi Ч Yau hypersurface in toric Kahler cone of 148
 and its toric blow-up, Calabi Ч Yau hypersurface in toric Kahler moduli of 148 269 and its toric blow-up, Calabi Ч Yau hypersurface in toric Kahler moduli of 148 269
 and its toric blow-up, GKZ decomposition of 50 124 146 and its toric blow-up, GKZ decomposition of 50 124 146
 and its toric blow-up, Mirror Conjecture for 269 and its toric blow-up, Mirror Conjecture for 269
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in 88 95 103 123 145 164 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in 88 95 103 123 145 164
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in A-system of 96 385 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in A-system of 96 385
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in discriminant locus of 147 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in discriminant locus of 147
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Frobenius method 165 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Frobenius method 165
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Gauss Ч Manin connection of 269 385 386 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Gauss Ч Manin connection of 269 385 386
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Hodge numbers of 146 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Hodge numbers of 146
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in homogeneous coordinate ring of 89 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in homogeneous coordinate ring of 89
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in moduli coordinates of 89 95 148 158 387 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in moduli coordinates of 89 95 148 158 387
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in monodromy of 270 385 387 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in monodromy of 270 385 387
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in periods of 164 165 385 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in periods of 164 165 385
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Picard Ч Fuchs equations of 90 96 103 158 165 385 386 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Picard Ч Fuchs equations of 90 96 103 158 165 385 386
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in satisfies integrality conjecture 270 385 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in satisfies integrality conjecture 270 385
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in simplified moduli of 147 148 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in simplified moduli of 147 148
 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Yukawa couplings of 103 104 125 385 388 and its toric blow-up, mirror of Calabi Ч Yau hypersurface in Yukawa couplings of 103 104 125 385 388
 and its toric blow-up, polytope of 88 and its toric blow-up, polytope of 88
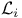 see УCotangent line see УCotangent line  Ф Ф
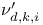 358 373 358 373
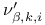 364 (see also 364 (see also 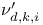
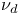 for for 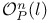 337 340 344 337 340 344
 for a concavex bundle 349 351 358 375 for a concavex bundle 349 351 358 375
 for quintic threefold 181 184 201 288 299 302 332 for quintic threefold 181 184 201 288 299 302 332
 in multiple cover case 352 in multiple cover case 352
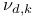 357 358 360 357 358 360
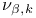 364 (see also 364 (see also 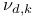
 -Euler data see УEuler dataФ -Euler data see УEuler dataФ
 -convex see У -convex see У
A-discriminant 122 125
A-hypergeometric equations see УA-systemФ
A-model 7 422 423
A-model is a (l + 1)-dimensional TQFT 434
A-model, connection 82 111 258 259 265Ч267 271
A-model, connection has maximally unipotent monodromy 250
A-model, connection of a Calabi Ч Yau threefold 248 255Ч257 318 328 329
A-model, connection, asymptotics of 245
A-model, connection, canonical extension of 249 251 254 316
A-model, connection, convergence assumption 245 249 261 316
A-model, connection, definition of 244
A-model, connection, flat sections of 248 249 315Ч318
A-model, connection, flatness of 244
A-model, connection, monodromy of 246 248 249 316
A-model, connection, monodromy weight filtration of 249 250 253
A-model, connection, Picard Ч Fuchs operator for see УPicard Ч Fuchs operatorФ
A-model, connection, role of basis 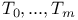 251 251
A-model, connection, satisfies integrality conjecture 250 258
A-model, correlation function see УCorrelation function A-modeФl
A-system 90 (see also УGKZ system and hypergeometric equationsФ)
A-system of a Calabi-Yau toric hypersurface see УCalabi Ч Yau toric
A-system of a smooth Fano toric variety 390 391
A-system, definition of 91
A-system, example of 93Ч96 125 162
A-system, holomorphic solution at maximally unipotent boundary point 160
A-system, solutions of 98 100 164
A-variation of Hodge structure 25 107 222 253 254 connectionФ)
A-variation of Hodge structure, definition of 251 255
A-variation of Hodge structure, Griffiths transversality for 252 254
A-variation of Hodge structure, Hodge filtration of 251
A-variation of Hodge structure, integer lattice of 249 251 254 260
A-variation of Hodge structure, middle 258
A-variation of Hodge structure, middle has maximally unipotent monodromy 255
A-variation of Hodge structure, middle, definition of 255
A-variation of Hodge structure, middle, mixed Hodge structure is Hodge Ч Tate 255 264
A-variation of Hodge structure, middle, real structure on 255 264
A-variation of Hodge structure, middle, toric 271
A-variation of Hodge structure, mixed Hodge structure of 253 255 connection monodromy
A-variation of Hodge structure, polarization of 252 254 258
Abel Ч Jacobi mapping 67 427
action 412 416
Action of sigma model 420 421
Action of sigma model, bosonic part of 420
Action of sigma model, fermionic part of 420
Algebraic space 170
Algebraic stack 169
Algebraic stack, bundle on see УEuler class stack
Algebraic stack, Deligne Ч Mumford 178
Algebraic stack, intersection theory on 178 279
Algebraic stack, quotient of 178
Algebraic stack, smooth 170 279
Almost complex structure 205 208
Almost complex structure, compatible 185 188
Almost complex structure, tamed 185
ample 33 35 40
Annihilation operator 415 418
Anticanonical divisor 46 48 49 51 54
Anticanonical linear system 55 56
Anticommutator 422
Arnold strange duality 401
B-model 8 422 423
B-model, correlation function see УCorrelation function B-modelФ
B-model, potential function 108 109 261 263
B-model, potential function in terms of periods 389 399
B-model, potential function of the quintic mirror see УQuintic mirror B-model
B-model, potential function, toric 269 388
Batyrev mirror see УMirror construction BatyrevФ
| Batyrev quantum ring 223 225 389
Batyrev quantum ring for 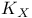 nef 393 nef 393
Batyrev quantum ring for 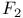 393Ч395 393Ч395
Batyrev quantum ring for 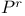 224 224
Batyrev quantum ring for a Fano toric variety 392
Batyrev quantum ring, definition of 224
Bipyramid construction 70 72
Birational cone conjecture see УCone conjecture birationalФ
Bivariant Chow group 180 182
Black holes 145 404
Black holes, massless 145
Boson 2 419 420 425
Bosonic components 427 429
Bosonic field 419
Bosonic variables 427 428
BRST cohomology 302 422 423
BRST operator 422 423
Caiabi-Yau cone 139
Caiabi-Yau cone, example of 140
Calabi Ч Yau, automorphism group of 12 127 129Ч131 138
Calabi Ч Yau, constructed from K3 surfaces 66
Calabi Ч Yau, generalized 65
Calabi Ч Yau, manifold 1 10 185 218 222 243 246 264Ч267 315 317 359 381 421 427
Calabi Ч Yau, manifold with K3 or elliptic fibration 404
Calabi Ч Yau, minimal 267
Calabi Ч Yau, moduli of see УModuliФ
Calabi Ч Yau, orbifold 12 17 55 408 410
Calabi Ч Yau, rigid 65 261 267
Calabi Ч Yau, threefold 3 4 6 7 9 10 53 74 79 102Ч112 130 132Ч134 143 151 201Ч210 225Ч227 238 247 248 251 255Ч262 267 282 288Ч293 308 318 325Ч329 352 366 388 389 405 423 425 427 A-model;
Calabi Ч Yau, toric complete intersection see УToric complete intersection Calabi
Calabi Ч Yau, toric hypersurface 53 56 60 116Ч127 134Ч143 155Ч166 267 270 383 430
Calabi Ч Yau, toric hypersurface, A-system of 91Ч93
Calabi Ч Yau, toric hypersurface, complex moduli of see УModuli complexФ
Calabi Ч Yau, toric hypersurface, Kahler moduli of see УModuli KahlerФ
Calabi Ч Yau, toric hypersurface, nondegenerate 122
Calabi Ч Yau, toric hypersurface, Picard Ч Fuchs equations of 91 92 383
Calabi Ч Yau, variety 55 60 63 407
Calabi Ч Yau, variety, definition of 11
Calabi Ч Yau, variety, minimal 11 55 63 116 407 409 410
Calabi Ч Yau, weighted projective hypersurface 70 207 405
Calabi Ч Yau, weighted projective hypersurface, list of 55 60 72 145
Canonical extension 75 154 247 249 260
Canonical extension of A-model connection see УA-model connection canonical
Categorical quotient 37
Cauchy Ч Riemann equation 185 187 191
Cauchy Ч Riemann equation, inhomogeneous 187
Cauchy Ч Riemann equation, perturbed 187
Cayley trick 64
Central charge 310 425
Chiral ring 36 217 427
Chiral superfield 426Ч428
Chow quotient 117 119 120 148
Class  see УMirror theorems Givental class see УMirror theorems Givental class
Clemens conjecture 15 16 202 206 214 400
Clemens conjecture, statement of 202
Cohomological field theory 241 (see also УDubrovin formalismФ)
Cohomological field theory for higher genus 241
Cohomological field theory, correlation functions of 241
Cohomological field theory, Kunneth formula for 241
Combinatorial duality 42 46
Complete intersection 364
Complete intersection in 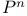 215 364 215 364
Complete intersection in a convex variety 366
Complete intersection in a convex variety nef 365
Complete intersection in a flag manifold see УComplete intersection in a convex varietyflag manifoldФ
Complete intersection in a Grassmannian see УGrassmannianФ
Complete intersection toric see УToric complete intersectionФ
Complete intersection virtual fundamental class of see УVirtual fundamental class of
Complex reflection 408
Complexified, Kahler class 3 6Ч9 11 12 15 18 22 204 217 218 225 228 230 303 304 434
Complexified, Kahler moduli see УModuli KahlerФ
Complexified, Kahler space 12 18 127 128 152 243 245 251
Concave bundle 349
Concave bundle in multiple cover case 352
Concavex bundle 337 349 350 352
Concavex bundle, critical 350 352
Concavex bundle, critical, definition of 351
Cone conjecture 130 134 150 152 245 399
Cone conjecture, birational 133
Cone conjecture, consequences of 130
Cone conjecture, when known 130
Cone, Calabi Ч Yau see УCalabi Ч Yau coneФ
Cone, dual see УDual coneФ
Cone, face of see УFace of a coneФ
Cone, Gorenstein 64
Cone, Gorenstein, reflexive see УReflexive Gorenstein coneФ
Cone, homogeneous self-adjoint 131
Cone, rational polyhedral see УRational polyhedral coneФ
Conformai algebra 2 423 424
Conformal field theory 423Ч426
Conformal field theory of a sigma model 425
Conformal field theory, gauge choice in 424
Conformal field theory, gauge group of 424
Conformal group 424 425
Conformal invariance 420 424
Conifold 122 143
Conifold, transition 143 404Ч406 type
Conifold, transition, example of 144
Conjugate momentum 412 414
Connection 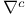 247 (see also УA-model connectionФ) 247 (see also УA-model connectionФ)
Connection 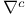 , flat sections of 247Ч249 254 316 318 , flat sections of 247Ч249 254 316 318
Connection matrix 25 27 76 79 106 108 246
Conserved current 419
Convex function 39 (see also У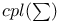 Ф) Ф)
Convex function, strictly 39 42 43 45
Convex, bundle 349 (see also УConcavex bundleФ)
Convex, line bundle 364
Convex, variety 298 358 365 366 381 382
Convex, variety, definition of 180
Correlation function 1 6 56 152 158 241 260 303 364 416 421
Correlation function of a Frobenius algebra 432
Correlation function, A-model 7Ч9 11 107 203 259 266 268 385 387 389 422 423 A-model
Correlation function, A-model of a Calabi Ч Yau threefold 204 226 255 256 327
Correlation function, A-model, definition of 221
Correlation function, A-model, effect of a flop 227
Correlation function, A-model, in terms of instanton numbers 226
Correlation function, B-model 8 9 110 256 259 265 268 385 387 423 potential
Correlation function, B-model, toric 268
Correlation function, genus g 434
Correlation function, n-point 416 434
Correlation function, quintic see УQuintic mirror and quintic threefoldФ
Correlation function, three-point 6Ч10 221 226 227 255 256 422
Correlation function, Voisin Ч Borcea mirror construction 69
Cotangent complex 178
Cotangent line 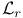 302 369 302 369
Creation operator 415 418
Crepant 54
Critical bundle see УConcavex bundle criticalФ
Curvature tensor 420
D-brane 402 404
Deformations, example of 125 147 158 159
Deformations, infinitesimal 57 153 175
Deformations, infinitesimal of a minimal Calabi Ч Yau orbifold 410
Deformations, infinitesimal of an orbifold 410
Deformations, non-polynomial 58 147
Deformations, polynomial 57 61
Deformations, principal component 122 125
Discriminant locus 104 122 toric nondegenerateФ)
Dominance conjecture 117 155
Double covers of 6-nodai quintics 293Ч297
Double covers of 6-nodai quintics, contribution to Gromov Ч Witten invariant and virtual fundamental class 297
Double covers of 6-nodai quintics, covers factoring through normalization 295Ч297
Double covers of 6-nodai quintics, covers not factoring through normalization 295 296
Double covers of 6-nodai quintics, moduli of 295
Double covers of 6-nodai quintics, moduli of tangent space of 296
Dual cone 31
Dualizing sheaf 11 46 407 409
Dubrovin connection 239 311 312
Dubrovin connection, definition of 239
Dubrovin connection, Euler vector field of 241
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



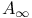 -category
-category 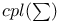
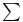 -convex
-convex 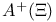
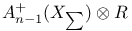


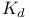
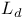

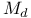

 to
to 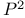
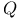
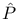
 and its toric blow-up
and its toric blow-up 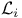
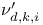
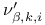
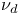 for
for 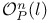
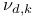
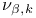
 -Euler data
-Euler data  -convex
-convex 
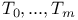
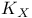 nef
nef