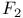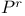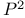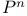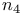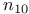|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cox D., Katz S. Ч Mirror symmetry and algebraic geometry |
|
|
 |
| ѕредметный указатель |
Mirror theorems, Givental, how to find change of variables 359
Mirror theorems, Givental, quintic 26 361Ч363
Mirror theorems, Givental, recursion lemma 369 371 372 374 37 378 380
Mirror theorems, Givental, regularity lemma 369 373 375 378
Mirror theorems, Givental, toric 381 382 387 389 391 405 small of
Mirror theorems, Givental, uniqueness lemma 378 380
Mirror theorems, Lian Ч Liu Ч Yau 28 263 332 334 349 354 380 398
Mirror theorems, Lian Ч Liu Ч Yau, application to multiple covers 355
Mirror theorems, Lian Ч Liu Ч Yau, toric 398
Mirror theorems, quintic 24Ч29 263 332 334 352 354 362
Mirror transformation see УEuler data linked mirror mirror
Missing mirrors 72
Moduli 1 5
Moduli, complex 3Ч5 9 56 81 82 113Ч128 131 144 148 149 264 423
Moduli, complex of a Calabi Ч Yau threefold 78 79 82 102 105 107 109 121 257 258 260
Moduli, complex of a Calabi Ч Yau toric hypersurface 92 93 116Ч127
Moduli, complex, 1-dimensional 78 79 82 84 87 102 105 107 109 257
Moduli, complex, compactification of 114 115 117 119Ч121
Moduli, complex, coordinates 114 123 124 155 159 267
Moduli, complex, dimension of 118 119
Moduli, complex, example of 123Ч127 139 147
Moduli, complex, Kahler 3Ч5 11 12 56 82 116 127Ч149 152 218 245 264 423
Moduli, complex, Kahler of a Calabi Ч Yau threefold 132Ч134 142 257 258
Moduli, complex, Kahler, 1-dimensionai 149
Moduli, complex, Kahler, boundary 143
Moduli, complex, Kahler, compactification of 132 135 136 142Ч144 152
Moduli, complex, Kahler, coordinates 128 129 267
Moduli, complex, Kahler, enlarged 132Ч134 136 142
Moduli, complex, Kahler, example of 139Ч142 146
Moduli, complex, Kahler, global 142
Moduli, complex, Kahler, large radius limit point see УLarge radius limit pointФ
Moduli, complex, Kahler, of a Calabi Ч Yau toric hypersurface 134Ч143
Moduli, complex, Kahler, partial compactification of 128Ч132 134 138 141 142 150
Moduli, complex, Kahler, toric 60 120 134 135 138 141 155 156 267 271
Moduli, complex, maximally unipotent boundary point see УMaximally unipotent boundary
Moduli, complex, polynomial 61 116Ч119 124Ч126 138 147 383 427
Moduli, complex, SCFT 3Ч5 128 144 145 264 401
Moduli, complex, SCFT, example of 147
Moduli, complex, simplified 95 117Ч127 135 138 142 155 156 267 271
Moduli, complex, stable maps see УStable maps moduli
Moment map 41 44 45 49 143 429
Moment map, example of 50
Monodromy theorem 75
Monodromy transformation 75 77 81 114 316
Monodromy transformation of A-model connection see УA-model connection monodromy
Monodromy transformation, logarithm of 75 81 111 114 142 246 247 249 316
Monodromy transformation, quasi-unipotent 75
Monodromy transformation, unipotent 75 77 78 114 246 247
Monodromy transformation, unipotent, maximaliy see УMaximally unipotentФ
Monodromy weight filtration 76 80 81 104 105 115 149 150 154 161 250 268
Monodromy weight filtration of the A-model connection see УA-model connection monodromy
Monomial ordering 225
Monomial-divisor mirror map 57 60 158 268 271 272
Mori cone 39 98 228
Mori cone of a toric variety see УToric variety Mori
Movable cone 133 142
Movable cone, reflected 134 142
Multiple covers 202 207 209 288 343
Multiple covers of non-isolated curves 208
Multiple covers, contribution to Gromov Ч Witten, invariant 202 204 288Ч294 352
Multiple covers, contribution to Gromov Ч Witten, invariant, Lian Ч Liu Ч YauТs proof 355
Multiple covers, contribution to Gromov Ч Witten, invariant, PandharipandeТs proof 291Ч293
Multiple covers, contribution to Gromov Ч Witten, invariant, proof for d = 2 289Ч291
Multiple covers, contribution to virtual fundamental class 202 205 294
Multiple covers, elliptic 209 214 300
Multiple covers, of 6-nodal quintics 293 294
Multiple mirrors 45 60 121
Nef complete intersection see УToric complete intersection nefФ
Nef-partition 62 63 97 100
Nef-partition, dual 63
Nets of quadrics 366
Nilpotent orbit 254
Nilpotent orbit theorem 76
Node deformations 341
NoetherТs theorem 419
Non-linear sigma model see УSigma modelФ
Non-perturbative state 402
Non-renormalization theorem 7 8 423
Nonequivariant limit 28 346 350Ч354 357 366 372 379 380
Nonequivariant limit, definition of 276
Normal cone 172 174 177 178 181 360
Normal cone, intrinsic 178 179
Normal cone, intrinsic, example of 179
Normal cone, refines Euler class 173
Normal cone, virtual 177
Normalization exact sequence 290 292
Normalized 3-form 21 104Ч106 110 112 151 258 259 268 328 385 normalizedФ)
Normalized d-form 154
Novikov ring 229
Observable 1 2 36 414
Obstruction bundle 208 289 290 292 obstructionФ)
Obstruction space 175
Obstruction theory 178 300
Obstruction theory, perfect 174 180 299
Obstruction theory, perfect for virtual fundamental class 180
Obstruction theory, perfect, definition of 179
Obstruction theory, perfect, equivariant 299
Obstruction theory, perfect, example of 179
octahedron 51
Open conjectures 399 400
Open conjectures, Calabi Ч Yau threefold, B-model potential function in terms of  389 399 389 399
Open conjectures, Calabi Ч Yau threefold, Yukawa coupling in terms of  389 399 389 399
Open conjectures, complex geometry, integrality conjecture 82 399
Open conjectures, complex geometry, maximally unipotent boundary points in simplified moduli space 120 399
Open conjectures, convergence of quantum cohomology 218 400
Open conjectures, enumerative geometry, Clemens conjecture 202 400
Open conjectures, enumerative geometry, enumerative significance of a Gromov Ч Witten invariant 196 400
Open conjectures, enumerative geometry, symplectic definition of instanton numbers 208 400
Open conjectures, Kahler geometry, cone conjecture 130 399
Open conjectures, Kahler geometry, toric part of Kahler cone of a Calabi Ч Yau toric hypersurface 138 399
Open conjectures, Picard Ч Fuchs equations,  is a solution 101 399 is a solution 101 399
Open conjectures, Picard Ч Fuchs equations, missing equations in A-system 94 399
Open conjectures, relation between 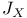 and and 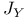 386 400 386 400
Open conjectures, virtual fundamental class for a complete intersection 386 400
Open conjectures, virtual fundamental class, equivalence of definitions 176 399
Operator product expansion 424 425
Orbifold 12 32 38 54 171 407
Orbifold, Calabi Ч Yau see УCalabi Ч Yau orbifoldФ
Orbifold, definition of 408
Orbifold, diffeomorphism 42 45 410
Orbifold, Goreilstein 407 408 410
Orbifold, Hodge theory on 409
Orbifold, infinitesimal deformations of 410
Orbifold, integration over 340
Orbifold, Kahler form on 409
Orbifold, symplectic 42 410
Orbifold, tangent sheaf of 410
Pair of pants 433 434
Partition function 310
path integral 416Ч418 422
Period 19 20 27 75 92 94 95 159 333 solutions
Period domain 254
Perturbative state 402
Phase transition 429
Phases 46 143
PhysicistТs Euler number 60 402 string
Picard Ч Fuchs equation 19 75 77 80 81 84 102 103
Picard Ч Fuchs equation of a Calabi Ч Yau threefold 79 105 327
Picard Ч Fuchs equation of a Calabi Ч Yau toric hypersurface see УCalabi Ч Yau toric
Picard Ч Fuchs equation of mirror of a Calabi Ч Yau toric complete intersection 100 101
Picard Ч Fuchs equation of the quintic mirror see УQuintic mirror Picard
Picard Ч Fuchs equation, computing via A-system see УA-systemФ
Picard Ч Fuchs equation, computing via Griffiths Ч Dwork method see УGriffiths Ч Dwork methodФ
Picard Ч Fuchs equation, examples of 87Ч90
Picard Ч Fuchs equation, missing equations in A-system 94 95 101 383 385 399
Picard Ч Fuchs equation, normalized 27 105Ч107
Picard Ч Fuchs equation, solutions of 19 96 101 149 156 160 161 263 268
Picard Ч Fuchs ideal 74 77 94
Picard Ч Fuchs ideal, associated  -module 74 75 101 -module 74 75 101
Picard Ч Fuchs operator 328 329
| Picard Ч Fuchs operator, gives relation in quantum cohomology 329
Picard Ч Fuchs operator, h-homogenization of 328 329
Picard Ч Fuchs operator, principal part of 328
Picard Ч Lefschetz transformation see УMonodromy transformationФ
PlanckТs constant h 413
Poincare duality 82 381
Poincare duality for orbifolds 171 172 183 305 408
Poisson bracket 413 414
Polytope 33
Polytope, facet of 33
Polytope, integral 33
Polytope, Newton 35 60
Polytope, normal fan of 34 51 53 135
Polytope, normalized volume 59
Polytope, polar 34 46 51 53 120
Polytope, polar, duality 35
Polytope, reflexive 60 (see also УReflexive polytopeФ)
Polytope, ring 34 36 37
Polytope, simplicial 409
Polytope, toric variety of 34
Potential function see УB-model potential
Prestable maps 179
Primitive cohomology 83 86 253 264 361
Primitive cohomology, definition of 74
Primitive collection 38 50 223Ч225
Primitive collection, ampleness criterion 40
Primitive contraction 132 143 148
Primitive contraction, Type I 133 134 143 144 147 226 227
Primitive contraction, Type II 133 134 143
Primitive contraction, Type III 133 134 143 146 227
Principal A-determinant 122
Projective subdivision 54 55 137
Projective subdivision, definition of 53
Projective subdivision, maximal 54Ч56 60 62 63 116 135 267 382
Projective subdivision, maximal, definition of 53
Projective subdivision, simplified 136 139Ч141 143 146
Projective subdivision, simplified, definition of 135
Pseudo-manifold 189
Quantization 10 413 415 418 419 424 425 430
Quantization, canonical 413 414
Quantization, radial 424
Quantum  -module 405 -module 405
Quantum anomaly 423Ч425
Quantum cohomology 7 25 82 101 200 422 430 435
Quantum cohomology of 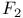 393Ч395 393Ч395
Quantum cohomology of 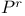 222 223 237 325 222 223 237 325
Quantum cohomology of a Calabi Ч Yau manifold 218 222 252
Quantum cohomology of a Calabi Ч Yau threefold 225Ч227 239 327 329
Quantum cohomology of a Grassmannian 227 405
Quantum cohomology of a smooth toric variety 223 390 392 393
Quantum cohomology of the quintic threefold 225 226 238
Quantum cohomology, big 229 230 304 312 314
Quantum cohomology, big, associativity of 232 234 237 WDW
Quantum cohomology, big, convergence of 230
Quantum cohomology, big, definition of 231
Quantum cohomology, big, degree condition for 235
Quantum cohomology, big, Kunneth formula for 234
Quantum cohomology, big, of 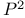 237 237
Quantum cohomology, big, of a Calabi Ч Yau threefold 239
Quantum cohomology, big, of the quintic threefold 238
Quantum cohomology, big, relation to small quantum product 242 243
Quantum cohomology, big, restriction of 242Ч244 314 320 327
Quantum cohomology, big, ring structure of 233 (see also УFrobenius algebraФ)
Quantum cohomology, big, used to define Givental connection 311
Quantum cohomology, coefficients 228Ч230
Quantum cohomology, definition of 218
Quantum cohomology, degree condition for 221 222
Quantum cohomology, effect of a flop 226 227
Quantum cohomology, gravitational see УGravitational quantum productФ
Quantum cohomology, modified 363
Quantum cohomology, modified, relations in 363
Quantum cohomology, of (l + 1)-dimensional TQFT 434
Quantum cohomology, other examples 227 228
Quantum cohomology, properties of 221
Quantum cohomology, relation to big quantum product 242 243
Quantum cohomology, relations in 321 322 325 364 387 390 392
Quantum cohomology, ring structure of 219 (see also УFrobenius algebraФ)
Quantum cohomology, small 217Ч228 230 314 315 320 326 359 363 364
Quantum cohomology, small, associativity of 219 228
Quantum cohomology, small, convergence of 218 227 228 244 245 400
Quantum cohomology, used to define A-model connection 243 244
Quantum corrections 12 18 148
Quantum differential equation 321 324 327 329 356 386 390 405
Quantum differential operator 321 322 329 392 395
Quantum differential operator, derived from relations in quantum cohomology 322 324
Quantum differential operator, example of 324 325 327
Quantum differential operator, gives relations in quantum cohomology 321 (see also УQuantum cohomology small relations
Quantum field theory 413Ч419 422 430
Quantum field theory, Hamiltonian formulation 416
Quantum field theory, Lagrangian formulation 416
Quantum field theory, two-dimensional 1
Quantum hyperplane section principle 26 364Ч366 405
Quantum hyperplane section principle for 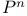 365 365
Quantum hyperplane section principle for a convex variety 365
Quantum hyperplane section principle, relation to Givental mirror theorem 366
Quasi-smooth 60 86 116 408
Quintic mirror 17 122 333
Quintic mirror, A-system of 93 94
Quintic mirror, A-system of, solutions of 101
Quintic mirror, B-model correlation function of 17 21Ч23 27 29 B-modelФ)
Quintic mirror, B-model potential function of 263 333
Quintic mirror, complex moduli of 18 262
Quintic mirror, construction of 17 61
Quintic mirror, Frobenius method 162
Quintic mirror, Gauss Ч Manin connection of 25
Quintic mirror, homogeneous coordinate ring of 62
Quintic mirror, monodromy of 111 112 262
Quintic mirror, Picard Ч Fuchs equation of 20 21 26 81 87 88 95 163 333
Quintic mirror, Picard Ч Fuchs equation of, solutions of 23 101 110 157 160 162 164 333 353 362
Quintic mirror, reflexive polytope of 61
Quintic mirror, satisfies integrality conjecture 82 110 150 157
Quintic mirror, Yukawa coupling of 21 157
Quintic mirror, Yukawa coupling of, normalized 21Ч23 2j| 110Ч111 262 363 B-model
Quintic threefold 15Ч29 352 429
Quintic threefold, 2875 lines on 23 24 157 173 281 282
Quintic threefold, 6-nodal quintics on 16 206 293 295 297
Quintic threefold, 6-nodal quintics on, normal bundle of 294
Quintic threefold, A-model correlation function of 15 16 22 23 27 28 203 226 262 333 363 A-modelФ)
Quintic threefold, big quantum cohomology of 238
Quintic threefold, Fermat 143 174
Quintic threefold, Gromov Ч Witten invariants of 173 174 201Ч203 293 332
Quintic threefold, Gromov Ч Witten invariants of equivariant 299
Quintic threefold, Gromov Ч Witten invariants of, formula for 184 201 281 332 350
Quintic threefold, Gromov Ч Witten invariants of, via localization 288
Quintic threefold, Gromov Ч Witten potential of 28 237 238 333 350 362 388
Quintic threefold, instanton numbers of 16 23Ч25 205 207 262 293 333 363
Quintic threefold, instanton numbers of, computation of 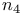 288 288
Quintic threefold, instanton numbers of, subtleties of 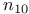 16 206 297 16 206 297
Quintic threefold, Kahler moduli of 15 18 22 157
Quintic threefold, mirror map of 18Ч20 22 23 26 28 110 156 157 162 263 333 353 362
Quintic threefold, mirror of see УQuintic mirrorФ
Quintic threefold, mirror symmetry for 15 18 20 22 23 262 263 288 333 quinticФ)
Quintic threefold, Mirror theorem see УMirror theorems quinticФ
Quintic threefold, rational curves on 1 15 16 24 202 206 288 293
Quintic threefold, small quantum cohomology of 225 226
Quintic threefold, virtual fundamental class of 173 180 181 184
Raising indices 218 239 417
Rational polyhedral cone 31
Rational polyhedral cone, strongly convex 31
Reciprocity lemma 344
Reconstruction theorem 196 197 200
Recursion lemma see УMirror theorems Givental recursion
Recursion relation, differential equations 95 162 163
Recursion relation, Gromov Ч Witten invariants see УGromov Ч Witten invariant computing recursionФ
Reflexive Gorenstein cone 62 64
Reflexive Gorenstein cone, duality of 64
Reflexive Gorenstein cone, index of 64
Reflexive Gorenstein cone, relation to nef-partitions 64
Reflexive Gorenstein cone, relation to reflexive polytopes 64
Reflexive polytope 6 35 47 53Ч55 63 96 116 118 134 135 144 145 155 267 382 383 405
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




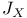 and
and 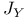
 -module
-module