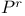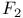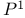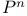|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cox D., Katz S. Ч Mirror symmetry and algebraic geometry |
|
|
 |
| ѕредметный указатель |
Gromov Ч Witten invariant, computing, other examples 201 214 405
Gromov Ч Witten invariant, computing, recursion for invariants of 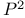 198 200 211 220 232 237 198 200 211 220 232 237
Gromov Ч Witten invariant, computing, recursion for invariants of 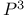 213 213
Gromov Ч Witten invariant, enumerative significance of 195 196 198 202 211 212 214 262 400 enumerative
Gromov Ч Witten invariant, equivalence of algebraic and symplectic definitions 195
Gromov Ч Witten invariant, equivariant 196 298Ч300 319
Gromov Ч Witten invariant, equivariant of quintic threefold 299
Gromov Ч Witten invariant, equivariant of zero section of equivariant bundle 299
Gromov Ч Witten invariant, equivariant, definition of 298
Gromov Ч Witten invariant, equivariant, nonequivariant limit of 298
Gromov Ч Witten invariant, symplectic definition 184 188Ч191 205 208 209
Gromov Ч Witten invariant, symplectic definition, equivalence of definitions 191 195
Gromov Ч Witten invariant, symplectic definition, intuitive idea of 186
Gromov Ч Witten invariant, symplectic definition, Li Ч Tian approach 190
Gromov Ч Witten invariant, symplectic definition, relation between mixed and symplectic invariants 190
Gromov Ч Witten invariant, symplectic definition, Ruan Ч Tian mixed invariant 188 189 210 212
Gromov Ч Witten invariant, symplectic definition, Ruan Ч Tian symplectic invariant 189 210 212
Gromov Ч Witten invariant, tree-level 196 230
Gromov Ч Witten invariant, used to define A-model correlation function 221
Gromov Ч Witten invariant, used to define Gromov Ч Witten potential 230
Gromov Ч Witten invariant, used to define quantum cohomology 218
Gromov Ч Witten potential 28 109 230Ч234 244 247 303 304 389
Gromov Ч Witten potential of a Calabi Ч Yau threefold 238 239 256 261 318 326
Gromov Ч Witten potential of a Calabi Ч Yau threefold, expressible in terms of periods of mirror 333 389
Gromov Ч Witten potential of a Calabi Ч Yau threefold, toric part of 389
Gromov Ч Witten potential of an elliptic curve 231 235
Gromov Ч Witten potential of the quintic threefold 28 237 238 333
Gromov Ч Witten potential, classical part 235
Gromov Ч Witten potential, definition of 230
Gromov Ч Witten potential, equivariant 319 320
Gromov Ч Witten potential, genus 0 free energy 231
Gromov Ч Witten potential, genus g 231
Gromov Ч Witten potential, homogeneity of 235
Gromov Ч Witten potential, of 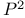 236 236
Gromov Ч Witten potential, quantum part 235
Gromov Ч Witten potential, structure of 234Ч236
Gromov Ч Witten potential, third partials of 231 234
Gromov Ч Witten potential, WDVV equation for 232Ч234 236 237 239
Gysin map 171
Gysin spectral sequence 59
Hamiltonian 412Ч415 430
Hamiltonian action 40 429
Hamiltonian action, moment map of see УMoment mapФ
Hamiltonian for electricity and magnetism 418
Hamiltonian vector field 40
HamiltonТs equations 413 414
Hard Lefschetz theorem 250 409
Heisenberg picture 413
HG of Euler data 346
HG of P 28 101 164 347 352Ч354 357
HG of Q 28 347 350 352Ч354 357
HG, definition of 346
HG, mirror transformation of 348 349 353 354 linked mirror
Hilbert scheme 208 282
Hirzebruch Ч Riemann Ч Roch theorem 175
Hochschild cohomology 403
Hodge diamond 4 5
Hodge numbers 4 6 66 227
Hodge numbers, Calabi Ч Yau toric complete intersection 63
Hodge numbers, Calabi Ч Yau toric hypersurface 56Ч60 119 145 146
Hodge numbers, string theoretic 60 63 273 402
Hodge structure of an orbifold 409
Hodge structure of weight k 73
Hodge structure, degeneration of 75
Hodge structure, Hodge filtration of 73 105 153
Hodge structure, Hodge filtration of limiting 76 111
Hodge structure, integer lattice of 73 76 260 268
Hodge structure, mixed 76 253
Hodge structure, mixed, Hodge Ч Tate 80 105 255 264 266 268
Hodge structure, mixed, Hodge Ч Tate, limiting 75 105 255 266
Hodge structure, polarized 74 107 253 258 267
Hodge structure, pure 59
Hodge structure, variation of 25 74 107 109 152 158 253 254 258 267
Hodge structure, variation of  -variation 268 271 272 -variation 268 271 272
Hodge structure, variation of formally degenerating 261
Hodge structure, variation of real 255 264
Hodge structure, variation of, comes from geometry 262
Hodge Ч Riemann bilinear relation 74 254 268
Hodge Ч Tate see УHodge structure mixed Hodge
Holomorphically symplectic 402
Homogeneous change of coordinates in the Mirror Theorem see УWeights of variablesФ
Hopf fibration 49
Hyper-Kahler 402
Hypergeometric equations 90Ч101 161 333
Hypergeometric functions 95 164
Hypergeometric functions, generalized 20
Hypergeometric functions, HG see УHGФ
Hypergeometric functions, p-adic 20
Indicial equation 77 79 80 163
Instanton number 8 203Ч210 226 308
Instanton number for quintic threefold see УQuintic threefold instanton
Instanton number, definition of 203
Instanton number, divisibility properties of 24
Instanton number, elliptic analog of 213 214
Instanton number, enumerative significance of 205Ч208
Instanton number, example of 205Ч208 (see also УQuintic threefold instanton
Instanton number, symplectic definition of 208Ч210 400
Instanton, corrections 9 423
Instanton, holomorphic 8 430
Instanton, naive 430
Instanton, sum 422 423
Instanton, worldsheet 422
Integrality conjecture 105Ч107 109 110 112 151 155 157 250 258 259 262 266 268 270 385 386 399
Integrality conjecture, statement of 82 150
Intersection homology 409
Intrinsic normal cone see УNormal cone intrinsicФ
Intrinsic normal sheaf 178 179 intrinsicФ)
J-holomorphic curve 209
J-holomorphic curve, definition of 208
J-holomorphic map 185
J-holomorphic map, moduli of, dimension of 186 187
J-holomorphic map, moduli of, fundamental class of 188
J-holomorphic map, moduli of, Li Ч Tian approach 188 190
J-holomorphic map, moduli of, Ruan approach 186
J-holomorphic map, moduli of, Ruan Ч Tian approach 187
J-holomorphic map, multiple cover 186
J-holomorphic map, perturbed 187 190 205
J-holomorphic map, simple 186 208 210
J-holomorphic map, stable 188
Jacobian ideal 84 86 90
Jacobian ring 427 428
Jones polynomial 435
K3 surface 359
K3 surface with involution 65Ч67
K3 surface, mirror symmetry for 401
K3 surface, rational curves on 400
K3 surface, vector bundles on 404
Kahler, cone 12 120 127 128 130 150 225 227 365
Kahler, cone of a Calabi Ч Yau threefold 132 144 146
Kahler, cone, behavior when complex structure varies 134
Kahler, cone, closure of 128 132 135 142 153 243 245 267 316 317 381
Kahler, cone, face of 132Ч134 144 146 158 227
Kahler, cone, locally polyhedral 132
Kahler, cone, polyhedral 39 129
Kahler, cone, simplicial 97
Kahler, cone, toric part of 135 136 138 139 399
Kahler, form on an orbifold 409
Kahler, moduli see УModuli KahlerФ
Kahler, space see УComplexified Kahler
Klein Ч Gordon equation 412 414 415 418
Kodaira Ч Spencer class 133
Kodaira Ч Spencer map 153
Kuranishi map 175 177
Lagrange lift 349 (see also УEuler data linked mirror
Lagrangian 1 412 420
Lagrangian category 403
Lagrangian density 411 412 414Ч416
Lagrangian density for electricity and magnetism 417 418
Lagrangian submanifold 403
Lagrangian submanifold, special 11 402 403
| Landau Ч Ginzburg, model 426
Landau Ч Ginzburg, orbifold 6 143 427 429
Landau Ч Ginzburg, potential 428
Landau Ч Ginzburg, theory 426Ч429
Large radius limit point 115 128Ч131 136 138 149 150 152 153 155 156 245 251 257 264 267 269
Large radius limit point, equivalence of 131 152
Large radius limit point, example of 141
Large radius limit point, tangent space at 158
Lattice of linear relations 39 41 44 136 138 140 155 159 224 390
Lattice of linear relations, example of 50 93 95 124 126 160 164
Lattice of linear relations, relation to ,4-system 91 97 99
Laurent monomial 35 118 126
Laurent polynomial 35 116 117 122 155
Lefschetz decomposition 259 264 361
Lefschetz Theorem 361
Left-moving, fermions 2 421
Left-moving, sector 425
Levi Ч Civita connection 420
Limiting weight filtration see УMonodromy weight filtrationФ
Linear circuit 136 138
Linear circuit, example of 136 140 141
Linear circuit, shrink the GKZ decomposition 139
Linear circuit, supported by a fan 137 139
Linear sigma model see УGauged linear sigma modelФ
Local operator 421 423
localization 279 280 366 382
Localization in  , fixed point loci 282 340 348 367 368 376 377 , fixed point loci 282 340 348 367 368 376 377
Localization in  , fixed point loci, description of 283 , fixed point loci, description of 283
Localization in  , fixed point loci, example of 284 285 289 , fixed point loci, example of 284 285 289
Localization in  , fixed point loci, graph of 283 289 290 367 368 370 , fixed point loci, graph of 283 289 290 367 368 370
Localization in  , fixed point loci, normal bundle of 285Ч287 289 291 293 370 equivariant of , fixed point loci, normal bundle of 285Ч287 289 291 293 370 equivariant of
Localization in  , fixed point loci, Type A graph 368 369 374 , fixed point loci, Type A graph 368 369 374
Localization in  , fixed point loci, Type B graph 368 374 , fixed point loci, Type B graph 368 374
Localization in  , torus action on 282 , torus action on 282
Localization of stacks 289
Localization theorem for equivariant cohomology 277 319 338 339 347Ч349
Localization theorem for polynomials in Chern classes 281 291Ч293
Localization theorem for smooth stacks 280 281 289 368 373 375 377
Localization theorem for the equivariant integral 279 335 339Ч342 345 348 376
Localization theorem, applications to enumerative geometry 282
Localization theorem, applied to 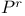 278 279 278 279
Localization theorem, computing instanton number  288 288
Localization theorem, computing lines on quintic threefold 282
Localization theorem, proving multiple cover formula 289
Lorentz transformation 415
Low energy limit 10
m(X) see УMori coneФ
Macaulay 297
Mathematical mirror pair 4 11 25 56 242 387 397
Mathematical mirror pair of Calabi Ч Yau threefolds 257Ч262
Mathematical mirror pair of Calabi Ч Yau threefolds in terms of correlation functions 259 262
Mathematical mirror pair of Calabi Ч Yau threefolds in terms of potential functions 260 262
Mathematical mirror pair of Calabi Ч Yau threefolds, definition of 258
Mathematical mirror pair, global 258
Mathematical mirror pair, higher dimensional 264Ч267
Mathematical mirror pair, higher dimensional for fourfolds 265 266
Mathematical mirror pair, higher dimensional, definition of 264
Mathematical mirror pair, higher dimensional, limitations of 265
Mathematical mirror pair, Hodge-theoretic 258 264
Mathematical mirror pair, quintic mirror and quintic threefold 262Ч263 333
Matrix integral 310
Matrix model 310
Maximal degeneracy 121 (see also УMaximally unipotent boundary
Maximal projective crepant partial desingularization 55
Maximal projective subdivision see УProjective subdivision maximalФ
Maximally unipotent, boundary point 82 93 102 104 105 109 110 113Ч115 119 121 128 131 138 149 151Ч156 159Ч161 251 257 266Ч269
Maximally unipotent, boundary point, definition of 81
Maximally unipotent, boundary point, equivalence of 115 120
Maximally unipotent, boundary point, example of 89 90 125 127 142
Maximally unipotent, boundary point, existence of 116 120 399
Maximally unipotent, boundary point, tangent space at 158
Maximally unipotent, monodromy 18 19 78Ч82 109 113 127 153 163 264
Maximally unipotent, monodromy, 1-dimensional moduli 78Ч81
Maximally unipotent, monodromy, r-dimensionai moduli 81Ч82
MaxwellТs equations 417 418
McKay correspondence 402
Minimal model 6
Minkowski sum 33 63
Mirror conjecture 328
Mirror conjecture for Calabi Ч Yau threefolds 258 261
Mirror conjecture for quintic threefold 262 333
Mirror conjecture, higher dimensional 267
Mirror conjecture, relation to Givental Mirror Theorem 383
Mirror conjecture, toric 112 267Ч273 383 Giventai toricФ)
Mirror conjecture, toric for threefolds 267
Mirror conjecture, toric, example of 269 270
Mirror conjecture, toric, higher dimensional 273
Mirror conjecture, toric, Hodge-theoretic 56 112 268 272 273 387
Mirror conjecture, toric, mathematical 271
Mirror conjecture, toric, statement of 268 272
Mirror construction 261
Mirror construction for Calabi Ч Yau complete intersections in flag manifolds 405
Mirror construction, Batyrev 53 56 60 70 72 120 123Ч125 135 139 143 144 146 148 155 261 267 268 271 272 381 383
Mirror construction, Batyrev Ч Borisov 62 63 100 147 405
Mirror construction, Batyrev, quintic threefold 61
Mirror construction, Greene Ч Plesser 53 56 89
Mirror construction, Voisin Ч Borcea 65 68Ч69 72 401 402
Mirror construction, Voisin Ч Borcea, complex and Kahler moduli 68 69
Mirror construction, Voisin Ч Borcea, relation to Batyrev construction 70
Mirror construction, Voisin Ч Borcea, Yukawa coupling 69
Mirror coordinates see УMirror mapФ
Mirror map 5 9 56 60 82 109 128 143 147Ч166 257 385
Mirror map for quintic threefold see УQuintic threefold mirror
Mirror map, definition of 150 157
Mirror map, definition of, choices to make 150 152 154
Mirror map, definition of, data needed to define 150
Mirror map, definition of, indeterminacy in definition 150
Mirror map, definition of, justification from physics 158
Mirror map, definition of, role of integrality conjecture 150 151
Mirror map, derivative of 152Ч154 158 266 267 definition choices
Mirror map, mirror coordinates 110 112 152 259 265
Mirror map, mirror coordinates, definition of 149
Mirror map, toric 148 151 155Ч159 267 268 270 272
Mirror map, toric for quintic threefold 156 157
Mirror map, toric, definition of 155 156
Mirror map, toric, not the identity 148
Mirror map, toric, resolving the lack of uniqueness 156
Mirror map, via hypergeometric functions 159Ч166
Mirror pair 5 6 9 53 56 402 421
Mirror pair, Hodge-theoretic see УMathematical mirror pair Hodge-theoreticФ
Mirror pair, mathematical see УMathematical mirror pairФ
Mirror pair, physics definition of 4
Mirror Symmetry 1 4Ч6 9 10 16 35 46 53 82 107 111 115 116 128 129 131 142 144 147 152 250 256 261 266 328 423 426
Mirror symmetry for a K3 surface 401
Mirror symmetry for gauged linear sigma models 430
Mirror symmetry for quintic threefold see УQuintic threefold mirror
Mirror symmetry for rigid Calabi Ч Yau 65
Mirror symmetry, categorical see УMirror symmetry homologicalФ
Mirror symmetry, classical 9 13 24 27 333 363 385
Mirror symmetry, earliest evidence for 60
Mirror symmetry, enumerative aspects of 214
Mirror symmetry, Hodge-theoretic 25 154 362 Hodge-theoreticФ)
Mirror symmetry, homological 11 403
Mirror symmetry, mathematical 11 112 217 242 257 274 397 402
Mirror symmetry, relation to Giventai mirror theorem 383
Mirror symmetry, toric 56
Mirror theorems 6 273 274
Mirror theorems, broader conception of 355 398 403
Mirror theorems, Givental 356 398
Mirror theorems, Givental for 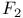 394 394
Mirror theorems, Givental for 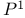 324 357 324 357
Mirror theorems, Givental for 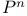 325 357 366 371 372 325 357 366 371 372
Mirror theorems, Givental for hypersurface in  383Ч386 388 383Ч386 388
Mirror theorems, Givental for nef complete intersection in 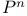 356 358 359 373 379 380 356 358 359 373 379 380
Mirror theorems, Givental, class  378Ч380 378Ч380
Mirror theorems, Givental, computes genus 0 gravitational, correlators 361
Mirror theorems, Givental, coordinate change lemma 379Ч381
Mirror theorems, Givental, double construction lemma 375 378 380
Mirror theorems, Givental, example of 359 364
Mirror theorems, Givental, genus 1 version 381
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



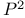
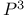
 -variation
-variation  , fixed point loci
, fixed point loci