|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stewart G.W. — Matrix algorithms. Volume 2: Eigensystems |
|
|
 |
| Предметный указатель |
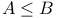 , A < B, etc. (componentwise comparison) 423 , A < B, etc. (componentwise comparison) 423
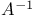 (inverse of A) 422 (inverse of A) 422
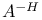 (conjugate transpose inverse of A) 422 (conjugate transpose inverse of A) 422
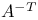 (transpose inverse of A) 422 (transpose inverse of A) 422
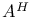 (conjugate transpose of A) 422 (conjugate transpose of A) 422
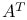 (transpose of A) 422 (transpose of A) 422
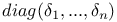 (diagonal matrix) 423 (diagonal matrix) 423
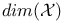 (dimension of (dimension of 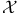 ) 424 ) 424
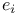 (ith unit vector) 423 (ith unit vector) 423
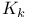 (A,u) (Krylov matrix) 267 (A,u) (Krylov matrix) 267
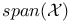 (the space spanned by (the space spanned by 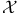 ) 424 ) 424
 -norm see “Norm” -norm see “Norm”
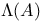 (the spectrum of A) 2 (the spectrum of A) 2
 (complex numbers) 421 (complex numbers) 421
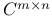 (space of complex (space of complex 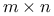 matrices) 421 matrices) 421
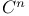 (complex n-space) 421 (complex n-space) 421
 (real numbers) 421 (real numbers) 421
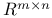 (space of real (space of real 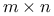 matrices) 421 matrices) 421
 (real n-space) 421 (real n-space) 421
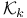 (A,u) (Krylov subspace) 267 (A,u) (Krylov subspace) 267
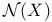 (null space of X) 424 (null space of X) 424
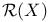 (column space of X) 424 (column space of X) 424
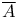 (conjugate of A) 422 (conjugate of A) 422
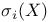 (the ith singular value of X) 204 (the ith singular value of X) 204
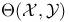 (canonical angle matrix) 248 (canonical angle matrix) 248
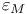 (rounding unit) 27 (rounding unit) 27
1-norm see “Norm”
2-norm see “Norm”
Abel, N.H. 55
Absolute norm see “Norm”
Accumulation of transformations 76
Aitken, A.C. 69 110
Algebraic multiplicity see “Eigenvalue”
angle see “Canonical angle”
Approximate Newton method 396
Approximate Newton method and inexact Newton method 419
Approximate Newton method, analysis 400—402
Approximate Newton method, constant shift approximation 403
Approximate Newton method, correction equation 397 420
Approximate Newton method, correction equation, inexact solution 403—404
Approximate Newton method, correction equation, solution 398
Approximate Newton method, correction formula 397
Approximate Newton method, derivation 396—397
Approximate Newton method, diagonally dominant A 403
Approximate Newton method, drawbacks 404—405
Approximate Newton method, equivalence of correction formula and equation 398
Approximate Newton method, error recurrence 402
Approximate Newton method, inner and outer iterations 403
Approximate Newton method, local convergence 402
Approximate Newton method, local convergence, convergence rates 402
Approximate Newton method, natural approximation 403
Approximate Newton method, orthogonal correction 399
Approximate Newton method, orthogonal correction, nomenclature 399
Arnoldi decomposition 297 299 315
Arnoldi decomposition, alternate form 300
Arnoldi decomposition, Arnoldi factorization 315
Arnoldi decomposition, computation see “Arnoldi method”
Arnoldi decomposition, computation of residuals 336
Arnoldi decomposition, hat convention 300
Arnoldi decomposition, QR factorization of Krylov sequence 298
Arnoldi decomposition, Rayleigh quotient 301
Arnoldi decomposition, reduced 299 302
Arnoldi decomposition, termination of Krylov sequence 300
Arnoldi decomposition, uniqueness 300
Arnoldi decomposition, uniqueness of starting vector 301
Arnoldi factorization see “Arnoldi decomposition”
Arnoldi method 117 344
Arnoldi method, Arnoldi process 302 303—304
Arnoldi method, block 344
Arnoldi method, comparison of implicit and Krylov — Schur restarting 332
Arnoldi method, computation of residuals 336
Arnoldi method, convergence criteria 334—336 347
Arnoldi method, convergence criteria, choice of tolerance 341—342
Arnoldi method, convergence criteria, shift-and-invert enhancement 336
Arnoldi method, deflation 337—340 347
Arnoldi method, deflation, advantages 337
Arnoldi method, deflation, in Arnoldi decomposition 340
Arnoldi method, deflation, in Krylov — Schur method 340
Arnoldi method, deflation, nonorthogonal bases 339—340
Arnoldi method, deflation, residual norm 337—338
Arnoldi method, deflation, stability 338—339
Arnoldi method, equivalence of implicit and Krylov — Schur restarting 331
Arnoldi method, filter polynomial 317 345
Arnoldi method, implicit restarting 318 345
Arnoldi method, implicit restarting, contraction phase 318—322
Arnoldi method, implicit restarting, double shift method 320
Arnoldi method, implicit restarting, exact (Rayleigh quotient) shifts 324—325
Arnoldi method, implicit restarting, example 323
Arnoldi method, implicit restarting, forward instability 325 346
Arnoldi method, implicit restarting, operation count 320—323
Arnoldi method, implicit restarting, overview 318
Arnoldi method, implicit restarting, the cycle 322
Arnoldi method, implicit restarting, truncation index 320
Arnoldi method, Krylov — Schur restarting 325—326 346
Arnoldi method, Krylov — Schur restarting, exchanging eigenblocks 326—328 me
Arnoldi method, Krylov — Schur restarting, operation count 329
Arnoldi method, Krylov — Schur restarting, the cycle 328—329
Arnoldi method, loss of orthogonality 117
Arnoldi method, operation count 304
Arnoldi method, reorthogonalization 303
Arnoldi method, restarted 316 344—345 implicit “Arnoldi Krylov
Arnoldi method, restarted, rationale 316
Arnoldi method, shift-and-invert enhancement 305
Arnoldi method, shift-and-invert enhancement, convergence criteria 336
Arnoldi method, shift-and-invert enhancement, stability 334 347
Arnoldi method, shift-and-invert enhancement, stagnation of Krylov subspace 305—306 316
Arnoldi method, stability 332—333 346—347
Arnoldi method, stability, shift-and-invert enhancement 334 347
Arnoldi method, storage requirements 304—305 316
Arnoldi, W.E. 315 344
ARPACK 325 345
ARPACK, convergence criteria 341
Arrowhead matrix 201
B inner product 371
B inner product, Cauchy inequality 371
B inner product, norm 371
B inner product, orthogonal matrix 372
B inner product, orthogonality 230 372
B inner product, orthogonalization 372—373
B inner product, orthogonalization, economizing B products 372—373
B inner product, orthogonalization, maintaining orthogonality 373
B inner product, orthonormal matrix 372
B inner product, symmetry 371
B-Arnoldi method 373
B-Arnoldi method, deflation 374
B-Arnoldi method, orthogonalization 373
B-Arnoldi method, residual norms 373—374
B-Arnoldi method, restarting 374
B-Arnoldi method, Ritz pairs 373
B-Lanczos method 374—375
B-Lanczos method, periodic reorthogonalization 375
B-Lanczos method, restarted 375
Backward error and unitary similarities 10
Backward error as paradigm 70
Backward error from residual 61 70 196 253 265 334—335 369
Backward error in convergence testing 10
Backward error, convergence criteria 62
Backward error, inverse power method 69
Backward stability and complex eigenvalues of real matrices 126
Backward stability, Arnoldi method 332—333 346—347
Backward stability, band tridiagonalization 189
Backward stability, bidiagonal QR step 220
Backward stability, deflation in Arnoldi method 338—339
Backward stability, divide-and-conquer algorithm for the spectral decomposition 183
Backward stability, double shift QR algorithm 126
Backward stability, eigenvector computation 102
Backward stability, Hessenberg QR algorithm 94
Backward stability, Householder’s reduction to tridiagonal form 162 170
Backward stability, implicit tridiagonal QR step 167
Backward stability, inertia of a tridiagonal matrix 192—193
| Backward stability, Lanczos algorithm with full orthogonalization 351
Backward stability, QZ algorithm 152
Backward stability, reduction to bidiagonal form 217
Backward stability, reduction to Hessenberg-triangular form 147
Backward stability, spectral decomposition updating 179
Backward stability, stability in the ususal sense 87
Backward stability, subspace iteration 388
Backward stability, Wilkinson’s contribution 111
Bai, Z. 23 129 346 395
Balancing 107—108 112
Balancing and grading 110
Balancing, matrix pencil 152—153 156
Balancing, operation count 108
Battels, R.H. 24
Bau, D. 23
Bauer, F.L. 394
Bellman, R 23
Beltrami, E. 226
Bhatia, R. 52
Bi-Lanczos algorithm 283 315 367
Bi-Lanczos algorithm, look-ahead recurrence 367
Bidiagonal matrix 215
Bidiagonal matrix, complex bidiagonal matrix to real 217
Bidiagonal matrix, reduction to 215—217 227
Bidiagonal matrix, reduction to, first column of the transformation 217
Bidiagonal matrix, reduction to, operation count 217
Bidiagonal matrix, reduction to, stability 217
Bidiagonal matrix, relative stability of singular values 217 223
Bidiagonal QR algorithm 217 227—228
Bidiagonal QR algorithm, combined with QR decomposition 226 228
Bidiagonal QR algorithm, combined with QR decomposition, operation count 226
Bidiagonal QR algorithm, combined with QR decomposition, pivoting 228
Bidiagonal QR algorithm, deflation 224
Bidiagonal QR algorithm, detecting negligible superdiagonal elements 223—224 227
Bidiagonal QR algorithm, graded matrices 224 227—228
Bidiagonal QR algorithm, QR step 219—220
Bidiagonal QR algorithm, QR step, operation count 220
Bidiagonal QR algorithm, QR step, stability 220
Bidiagonal QR algorithm, shift computation 222—223
Bidiagonal QR algorithm, zero shift 227
Biorthogonal bases 245
Bjoerck, A. 264
Block Krylov subspace see “Krylov subspace”
Block triangularization of nearly block triangular matrix 255
Braman, K 129
Bunch, J.R. 201
Byers, R. 129
Canonical angle 248 264
Canonical angle of a combination of subspaces 250—251
Canonical angle of a vector and a subspace 250
Canonical angle, angles between right and left eigenspaces 251
Canonical angle, between two vectors 44
Canonical angle, between two vectors, computation 49
Canonical angle, characterization of largest angle 249
Canonical angle, computation 249 264
Canonical angle, subspaces of unequal dimensions 249—250
Cauchy, A. 23
Cayley, A. 23
Chan, T.F. 228
Chandrasekaran, S. 235
Characteristic equation 4 24
Characteristic polynomial 4 24
Characteristic polynomial and companion matrix 55
Characteristic polynomial and terminating Krylov sequences 279
Characteristic polynomial in Lanczos’s method 315
Characteristic polynomial, matrix of order two 4—5
Characteristic value 23
Chatelin, F. 23 279
Chebyshev polynomial 271 280
Chebyshev polynomial as filter polynomial 317
Chebyshev polynomial in complex plane 280
Chebyshev polynomial in subspace iteration 392
Cholesky algorithm 157
Cholesky decomposition 231 426
Cholesky decomposition, pivoted 234
Cholesky decomposition, updating 171
Chordal distance 138 155
Clint, M. 394
Column space (’1Z(X)) 424
Column- and row-oriented algorithms 102 162
Companion matrix 55
Complete system of eigenvectors 2
Complete system of eigenvectors and diagonalization 8—9
Condition number see “Condition”
Condition, condition number 48
Condition, condition number, limitations 48
Condition, eigenvalue 48 53
Condition, eigenvalue, condition number 48
Condition, eigenvalue, Hermitian matrix 42—43 51
Condition, eigenvector 48—51 53
Condition, eigenvector, condition number 50
Condition, eigenvector, Hermitian matrix 51—52
Condition, generalized eigenvalue 140
Condition, generalized eigenvector 143
Condition, ill conditioning 48
Condition, S/PD generalized eigenvalue 231
Condition, simple eigenblock 260
Condition, simple eigenspace 261
Condition, singular values 206
Condition, singular vector 209—210
Condition, singular vector, condition number 210
Condition, well conditioning 48
Congruence transformation 190
Conjugate gradient method 279
Consistent norm see “Norm”
Convergence ratios 34
Convergence, normwise and componentwise 30
Crawford, C.R. 236
Cross-product algorithm for the S VD 210—211
Cross-product algorithm for the S VD, assessment 214 227
Cross-product algorithm for the S VD, attractive features 211
Cross-product algorithm for the S VD, inaccuracy in the left singular vectors 214
Cross-product algorithm for the S VD, inaccuracy in the right singular vectors 212—213
Cross-product algorithm for the S VD, inaccuracy in the singular values 211—212
Cross-product algorithm for the S VD, refined Ritz vector 291—292 296
Cross-product algorithm for the S VD, use by statisticians 227
Cross-product matrix 205
CS decomposition 236—237
CS decomposition, algorithms 237
Cullum, J. 280 367
Cuppen, J.J.M. 201
Curtis, A.R. 156
Datta, B.N. 23
Davidson, E.R. 419
Davidson’s algorithm 419
Davis, C. 53 265
Defectiveness 384
Defectiveness and Krylov subspaces 276
Defectiveness, dependence of eigenvectors 8
Defectiveness, dominant eigenvalues 34
Defectiveness, eigenvalue 7
Defectiveness, matrix 7 15
Defectiveness, sensitivity of eigenvalues 7—8 38
Definite generalized eigenvalue problem 235—236
Definite generalized eigenvalue problem, rotating to make B positive definite 236
Deflation 12 344 “Power “QR “Etc.”)
Deflation by inspection 106—107
Deflation by inspection, operation count 107
Deflation, complex eigenvector 114
Dembo, R.S. 419
Demmel, J.W. 23 129 227 346
Dennis, J.E. 265 418
Det(A) (determinant of A) 422
Dhillon, I.S. 202
Diagonalization, block 15 19—20
Diagonalization, block, assessment 25
Diagonalization, block, uniqueness 20
Diagonalization, complete system of eigenvectors 8—9
Diagonalization, distinct eigenvalues 20
Divide-and-conquer algorithm for the spectral decomposition 181—183 201
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



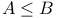 , A < B, etc. (componentwise comparison)
, A < B, etc. (componentwise comparison) 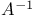 (inverse of A)
(inverse of A) 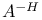 (conjugate transpose inverse of A)
(conjugate transpose inverse of A) 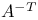 (transpose inverse of A)
(transpose inverse of A) 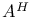 (conjugate transpose of A)
(conjugate transpose of A) 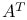 (transpose of A)
(transpose of A) 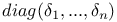 (diagonal matrix)
(diagonal matrix) 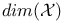 (dimension of
(dimension of 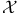 )
) 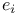 (ith unit vector)
(ith unit vector) 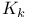 (A,u) (Krylov matrix)
(A,u) (Krylov matrix) 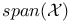 (the space spanned by
(the space spanned by  -norm
-norm 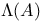 (the spectrum of A)
(the spectrum of A)  (complex numbers)
(complex numbers) 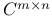 (space of complex
(space of complex 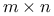 matrices)
matrices) 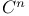 (complex n-space)
(complex n-space)  (real numbers)
(real numbers) 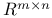 (space of real
(space of real  (real n-space)
(real n-space) 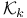 (A,u) (Krylov subspace)
(A,u) (Krylov subspace) 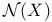 (null space of X)
(null space of X) 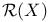 (column space of X)
(column space of X) 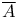 (conjugate of A)
(conjugate of A) 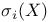 (the ith singular value of X)
(the ith singular value of X) 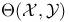 (canonical angle matrix)
(canonical angle matrix) 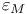 (rounding unit)
(rounding unit)