|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stewart G.W. Ч Matrix algorithms. Volume 2: Eigensystems |
|
|
 |
| ѕредметный указатель |
Hessenberg QR algorithm, explicit shift algorithm, stability 98
Hessenberg QR algorithm, forward instability 325 346
Hessenberg QR algorithm, Francis double shift 115 148
Hessenberg QR algorithm, implementation issues 112
Hessenberg QR algorithm, implicit double shift 87 110 118Ч123 128
Hessenberg QR algorithm, implicit double shift, general strategy 118
Hessenberg QR algorithm, implicit double shift, real Francis shifts 119
Hessenberg QR algorithm, implicit double shift, starting 118Ч119
Hessenberg QR algorithm, implicit Q theorem 118 me
Hessenberg QR algorithm, invariance of Hessenberg form 92 112
Hessenberg QR algorithm, multishift 128Ч129
Hessenberg QR algorithm, transmission of shifts 112
Hessenberg QR algorithm, Wilkinson shift 97 112
Hessenberg QR algorithm, Wilkinson shift, computation 97Ч98
Hessenberg-triangular form 144Ч147 156
Hessenberg-triangular form, operation count 147
Hessenberg-triangular form, stability 147
Higham, D.J. 380
Higham, N.J. 24 228 380
Hilbert, D. 23
Hoffman Ч Wielandt Theorem 43 169
Horn, R.A. 23
Horowitz, L. R 203
Hotelling, H. 69
Householder transformation 12 81 111
Householder transformation, product with a matrix 81Ч82
Householder transformation, reduction of a vector to multiple of 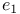 82Ч83 82Ч83
Householder transformation, reduction of a vector to multiple of 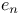 82Ч83 82Ч83
Householder transformation, reduction of real vectors 83
Householder transformation, reduction of row vectors 82
Householder, A.S. 23 111 279
Hump, the 34
I (cross matrix) 423
I, 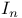 (identity matrix) 423 (identity matrix) 423
Implicit Q theorem 116 118
Inertia 190 201
Inertia and LU decomposition 191
Inertia of a tridiagonal matrix 191Ч193
Inertia of a tridiagonal matrix, operation count 192
Inertia of a tridiagonal matrix, stability 192Ч193
Inertia, computed by Gaussian elimination 191
Inertia, invariance under congruence transformations 190
Inf(X) (smallest singular value of X) 205
Interlacing theorem 42
Interval bisection 193
Invariant subspace see УEigenspaceФ
Inverse power method 66 70Ч71 170
Inverse power method, backward error 69
Inverse power method, convergence 68
Inverse power method, dominant eigenvector 56
Inverse power method, effects of rounding error 68Ч69
Inverse power method, implementation 67
Inverse power method, residual computation 66Ч67
Inverse power method, symmetric band matrix 195Ч200
Inverse power method, use of optimal residuals 71
Ipsen, I.C.F. 70 265
Jacobi Ч Davidson method 296 381 396 404 405 419Ч420
Jacobi Ч Davidson method, compared with approximate Newton method 406
Jacobi Ч Davidson method, convergence testing 408Ч409
Jacobi Ч Davidson method, convergence to more than one vector 407
Jacobi Ч Davidson method, convergence to more than one vector, retarded by inexact solution 417Ч418
Jacobi Ч Davidson method, correction equation 420
Jacobi Ч Davidson method, DavidsonТs algorithm 419
Jacobi Ч Davidson method, derivation from approximate Newton method 404Ч405
Jacobi Ч Davidson method, exact solution of correction equation 415Ч416
Jacobi Ч Davidson method, exact solution of correction equation, restriction on choice of shifts 415Ч416
Jacobi Ч Davidson method, extending partial Schur decompositions 407Ч411
Jacobi Ч Davidson method, focal region 405
Jacobi Ч Davidson method, harmonic Ritz vectors 411Ч412
Jacobi Ч Davidson method, Hermitian matrices 412Ч414 420
Jacobi Ч Davidson method, iterative solution of correction equation 416Ч418
Jacobi Ч Davidson method, iterative solution of correction equation, free choice of shifts 416Ч417
Jacobi Ч Davidson method, iterative solution of correction equation, Krylov sequence methods 416
Jacobi Ч Davidson method, iterative solution of correction equation, preconditioning 416
Jacobi Ч Davidson method, iterative solution of correction equation, stopping 417Ч418
Jacobi Ч Davidson method, OlsenТs method 419Ч420
Jacobi Ч Davidson method, operation count 409
Jacobi Ч Davidson method, orthogonalization 409
Jacobi Ч Davidson method, partial Schur decomposition 407
Jacobi Ч Davidson method, residual computation 408Ч409
Jacobi Ч Davidson method, restarting 411
Jacobi Ч Davidson method, restarting, with harmonic Ritz vectors 412
Jacobi Ч Davidson method, shift parameters 405Ч406
Jacobi Ч Davidson method, solving projected systems 414Ч415
Jacobi Ч Davidson method, solving projected systems, ill conditioning 415
Jacobi Ч Davidson method, solving projected systems, multiple right-hand sides 414Ч415
Jacobi Ч Davidson method, storage requirements 409
Jacobi Ч Davidson method, updating the Rayleigh quotient 409
Jacobi, C.G.J. 201 202 403 420
JacobiТs method 202Ч203
JacobiТs method and graded matrices 203
JacobiТs method as preprocessing step 202
JacobiТs method, convergence 202
JacobiТs method, convergence, cyclic method 203
JacobiТs method, convergence, quadratic 203
JacobiТs method, parallelism 203
JacobiТs method, rediscovery 202
JacobiТs method, threshold method 203
Jennings, A. 394 395
Jensen, P.S. 347 380
Jia, Z. 295 296
Jiang, E. 170 265
Johnson, C.R. 23
Jordan block see УJordan canonical formФ
Jordan canonical form 21 24Ч25 36
Jordan canonical form, assessment 22 25
Jordan canonical form, Jordan block 7 20
Jordan canonical form, Jordan block, powers of 34Ч35
Jordan canonical form, principal vector 22
Jordan canonical form, sensitivity of eigenvalues 38
Jordan canonical form, uniqueness 21
Jordan, C. 155 226 264
Kahan, W. 53 156 170 201 227 264 265
Kaniel, S. 280
Kato, T. 52
Kline, M 23
Koenig, J. 110
Kogbetliantz, E.G. 228
Kollerstrom, N. 418
Krause, G. 52
Kronecker product 24
Kronecker, L. 155
Krylov decomposition 297 309.316
Krylov decomposition, computation of harmonic Ritz vectors 314Ч315
Krylov decomposition, computation of refined Ritz vectors 314
Krylov decomposition, computation of residuals 335
Krylov decomposition, economics of transforming 312Ч314
Krylov decomposition, equivalence 309
Krylov decomposition, equivalence, to an Arnoldi decomposition 311Ч312
Krylov decomposition, nomenclature 310
Krylov decomposition, orthonormal 309
Krylov decomposition, Rayleigh quotient 309
Krylov decomposition, reduction to Arnoldi form 312Ч314
Krylov decomposition, similarity 310
Krylov decomposition, translation 311
Krylov subspace 267 279 УKrylov УLanczos
Krylov subspace and defective matrices 276
Krylov subspace and scaling 268
Krylov subspace and similarity transformations 268
Krylov subspace, block 277. 280 367
Krylov subspace, block Krylov sequence 277
Krylov subspace, block, computation 277
Krylov subspace, block, convergence 277
Krylov subspace, block, non-Hermitian matrices 278
Krylov subspace, compared with power method 266
Krylov subspace, convergence 269 279Ч280 315
Krylov subspace, convergence, assessment of polynomial bounds 274
Krylov subspace, convergence, multiple eigenvalues 273Ч274
Krylov subspace, convergence, polynomial bounds 269Ч272
Krylov subspace, convergence, square root effect 272Ч273
| Krylov subspace, convergence, to inferior eigenvector 273
Krylov subspace, convergence, to interior eigenpairs 273
Krylov subspace, convergence, to the subdominant eigenvector 266
Krylov subspace, degeneracy in Krylov sequence 298
Krylov subspace, elementary properties 267Ч268
Krylov subspace, invariance under shifting 268
Krylov subspace, Krylov matrix 267
Krylov subspace, Krylov sequence 266 279
Krylov subspace, multiple eigenvalues 277
Krylov subspace, multiple eigenvalues, convergence 273Ч274
Krylov subspace, multiple eigenvalues, deflation 278
Krylov subspace, non-Hermitian matrices, convergence 274Ч275 280
Krylov subspace, non-Hermitian matrices, polynomial bounds 275Ч276
Krylov subspace, polynomial representation 268
Krylov subspace, termination 268
Krylov subspace, termination, and characteristic polynomial 279
Krylov subspace, termination, and eigenspaces 269
Krylov subspace, uniqueness of starting vector 301
Krylov, A.N. 279
Kublanovskaya, V.N. 110
Lagrange, J.-L. 23
Lanczos algorithm 279 315
Lanczos algorithm and characteristic polynomial 315
Lanczos algorithm and Rayleigh Ч Ritz method 348
Lanczos algorithm as iterative method 365
Lanczos algorithm, adjusted Rayleigh quotient 351
Lanczos algorithm, adjusted Rayleigh quotient, updating 362Ч363
Lanczos algorithm, block 280 367
Lanczos algorithm, computing residual norms 363
Lanczos algorithm, estimating loss of orthogonality 356Ч358
Lanczos algorithm, filter polynomial 352
Lanczos algorithm, filter polynomial, Chebyshev polynomial 365
Lanczos algorithm, filter polynomial, Leja points 365
Lanczos algorithm, full reorthogonalization 349 365
Lanczos algorithm, full reorthogonalization, convergence and deflation 352
Lanczos algorithm, full reorthogonalization, error analysis 365
Lanczos algorithm, full reorthogonalization, essential tridiagonality of Rayleigh quotient 351
Lanczos algorithm, full reorthogonalization, implicit restarting 351Ч352 365
Lanczos algorithm, full reorthogonalization, Krylov-spectral restarting 352 365
Lanczos algorithm, full reorthogonalization, stability 351
Lanczos algorithm, global orthogonality 350
Lanczos algorithm, Lanczos decomposition 297 307
Lanczos algorithm, Lanczos decomposition, Rayleigh quotient 306
Lanczos algorithm, Lanczos decomposition, uniqueness 307
Lanczos algorithm, Lanczos recurrence 307Ч308 348
Lanczos algorithm, Lanczos recurrence, alternative 307 315
Lanczos algorithm, Lanczos recurrence, loss of orthogonality 308
Lanczos algorithm, Lanczos recurrence, operation count 308
Lanczos algorithm, Lanczos recurrence, storage considerations 308
Lanczos algorithm, local orthogonality 350
Lanczos algorithm, loss of orthogonality 348
Lanczos algorithm, loss of orthogonality, local and global 350
Lanczos algorithm, method of minimized iterations 279
Lanczos algorithm, no reorthogonalization 349 366
Lanczos algorithm, no reorthogonalization, software 366
Lanczos algorithm, partial reorthogonalization 350 365Ч366
Lanczos algorithm, partial reorthogonalization, software 366
Lanczos algorithm, periodic reorthogonalization 350 358Ч362 365Ч366
Lanczos algorithm, periodic reorthogonalization, example 364
Lanczos algorithm, periodic reorthogonalization, modified Gram Ч Schmidt algorithm 359
Lanczos algorithm, periodic reorthogonalization, software 366
Lanczos algorithm, Rayleigh quotient 347
Lanczos algorithm, Rayleigh quotient, contamination by reorthogonalization 350
Lanczos algorithm, reorthogonalization 348 365 full УLanczos no УLanczos partial УLanczos periodic УLanczos selective
Lanczos algorithm, reorthogonalization, and semiorthogonality 358Ч359
Lanczos algorithm, reorthogonalization, contamination of the Rayleigh quotient 350
Lanczos algorithm, reorthogonalization, difficulties 348Ч349
Lanczos algorithm, reorthogonalization, general algorithm 349Ч350
Lanczos algorithm, reorthogonalization, updating adjusted Rayleigh quotient 362Ч363
Lanczos algorithm, restarted 280
Lanczos algorithm, selective reorthogonalization 350 365Ч366
Lanczos algorithm, semiorthogonality 353 365Ч366
Lanczos algorithm, semiorthogonality, and reorthogonalization 358Ч359
Lanczos algorithm, semiorthogonality, effects of relaxing constraint 353
Lanczos algorithm, semiorthogonality, QR factorization 353Ч354
Lanczos algorithm, semiorthogonality, Rayleigh quotient 355
Lanczos algorithm, semiorthogonality, residual norms 355Ч356
Lanczos algorithm, semiorthogonality, Ritz vectors 355Ч356
Lanczos algorithm, semiorthogonality, size of reorthogonalization coefficients 354
Lanczos algorithm, singular value decomposition 366Ч367
Lanczos algorithm, termination and restarting 350
Lanczos algorithm, thick restarting 365
Lanczos decomposition see УLanczos algorithmФ
Lanczos recurrence see УLanczos algorithmФ
Lanczos, C. 279 315 365
LAPACK 112
LAPACK, 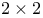 blocks in double shift QR algorithm 129 blocks in double shift QR algorithm 129
LAPACK, 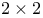 blocks in QZ algorithm 156 blocks in QZ algorithm 156
LAPACK, ad hoc shift in QR algorithm 105
LAPACK, bidiagonal QR algorithm 228
LAPACK, CS decomposition 237
LAPACK, differential qd algorithm 228
LAPACK, divide-and-conquer algorithm for the spectral decomposition 183
LAPACK, eigenvalues by bisection 202
LAPACK, eigenvectors by the inverse power method 202
LAPACK, eigenvectors of triangular matrices 102
LAPACK, exchanging eigenblocks 328 346
LAPACK, multishift QR algorithm 128 129
LAPACK, PWK method for the tridiagonal QR algorithm 171
LAPACK, reduction to tridiagonal form 170
LAPACK, S/PD generalized eigenvalue problem 235
LAPACK, spectral decomposition downdating 201
LAPACK, storage of band matrices 187
LAPACK, tridiagonal QR step 170
LAPACK, WilkinsonТs algorithm 233
Large matrices 239
Large matrices, storage of eigenvectors 239
Large matrices, storage of sparse matrices 239
Latent value 24
Le, J. 346
Left eigenpair 2
Lehoucq, R.B. 345 346
Lewis, J.G. 367
Li, C.K. 235
Local convergence ratio see УConvergence ratiosФ
LR algorithm 110 394
LR algorithm, convergence 111
LU decomposition 193 425
LU decomposition and inertia 191
Lui, Z.A. 367
Martin, R.S. 113
Mathias, R. 129 235 265
Matrix 421
Matrix powers  33Ч36 33Ч36
Matrix powers  , behavior when computed 36 , behavior when computed 36
Matrix powers  , spectral radius bounds 33 , spectral radius bounds 33
Matrix powers  , the hump 34 , the hump 34
Matrix, cross 423
Matrix, diagonal 423
Matrix, element 421
Matrix, full rank 425
Matrix, hermitian 423
Matrix, history 23
Matrix, identity 423
Matrix, order 422
Matrix, orthogonal 423
Matrix, orthonormal 423
Matrix, permutation 423
Matrix, sum and product 422
Matrix, symmetric 423
Matrix, trapezoidal 424
Matrix, triangular 424
Matrix, unit triangular, trapezoidal 424
Matrix, unitary 423
Matrix, zero 423
Matrix-vector product, effects of rounding error 65
Matrix-vector product, tridiagonal matrix 58Ч59
Meerbergen, K. 380
Method of minimized iterations 279
Moler, C.B. 156
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



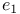
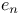
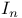 (identity matrix)
(identity matrix)  blocks in double shift QR algorithm
blocks in double shift QR algorithm 