јвторизаци€
ѕоиск по указател€м
Bogolubov N.N., Logunov A.A., Todorov I.T. Ч Introduction to Axiomatic Quantum Field Theory
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Introduction to Axiomatic Quantum Field Theoryјвторы: Bogolubov N.N., Logunov A.A., Todorov I.T.јннотаци€: At the end of 1960 we made plans to write a monograph about the general principles of quantum field theory and their experimental implications. We intended primarily to give an account of the progress of the theory of dispersion relations since the appearance of the book of Bogolubov, Medvedev and Polivanov ([BMP]. As an introduction we wanted to include a review of the various approaches to axiomatic field theory. This introduction had to cover not only the formulation of Bogolubov, Medvedev and Polivanov, based on the apparatus of functional derivatives of the 5-matrix and the condition of microcausality, but also the field formulation associated with the names of Wightman, Haag, Lehmann, Symanzik, Zimmermann, and others. In the course of the work the tasks (and with them the size) of the introduction grew larger and larger, until eventually it developed into this book.
язык: –убрика: ћатематика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 1975 оличество страниц: 707ƒобавлена в каталог: 18.04.2010ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
Spherical harmonics 202 Spin 111 150 153Ч158 161 167 175 184 185 316 318 322 Spin affinors 174 Spin, discrete-transformation phase conventions and 326Ч327 Spin, higher 241Ч242 337 343Ч349 352 353 576 Spin, superselection rule 122 250Ч251 Spin, TCP and 515Ч516 Spin-and-statistics theorem 4 252 337 474Ч477 526Ч538 576 Spin-and-statistics theorem for parafields 545Ч547 576 Spin-and-statistics theorem, infinite-component counterexamples 564Ч566 577 Spin-and-statistics theorem, nonlocal counterexample 511Ч512 Spin-and-statistics theorem, TCP theorem and 513 538 572Ч573 574Ч575 Spinor field 179 250Ч252 264Ч265 281Ч282 319Ч327 402Ч404 527 534 620Ч623 Spinor field in algebraic approach 600Ч601 Spinor field in functional differentiation 408Ч409 Spinor field, charge conjugation phase convention 345 Spinor field, free 313Ч319 Spinor field, functions associated with [S(x), etc.] 315 318Ч319 322 335 Spinor field, gauge transformation 404Ч406 Spinor field, Lagrangian 557 Spinor field, TCP transformation 499Ч504 Spinor field, TVEVs and 273 Spinors 122 168Ч169 241 247 Spinors, discrete transformations and 169Ч170 176Ч180 182Ч184 187 191-192 319Ч327 352 501Ч504 Spinors, four-component (Dirac spinors, bispinors) 168Ч192 241 314 321 340Ч342 516 529 Spinors, indices (dotted, etc.) 168Ч169 482Ч483 501-504 Spinors, infinite-component 565 St 577 666 Stability, of vacuum and one-particle states 368 380 407 411 432 442Ч443 452 Stapp, H. P. 467 671 Star algebra (*-algebra) 584Ч585 Star isomorphism 587 Star representation (*-representation) 569 States, State vectors 109 112Ч128 137Ч138 142 591 610 States, State vectors in algebra (Cfc* ) 591Ч595 598 States, State vectors in free field theories 303 306Ч308 316 States, State vectors of generalized free field 331Ч332 States, State vectors, discrete transformations and 323Ч327 States, State vectors, extremal invariant 625 States, State vectors, mixed and pure 591 States, State vectors, physically realizable 122Ч128 States, State vectors, space of 112Ч128 242 379 618Ч619 Statistical mechanics 625 Statistics 526 539 Steinmann identities, Steinmann quartets 360 446Ч449 467 Steinmann, O. 392 446 464 466 467 651 671 672 Stieltjes integral 20 88 Stone, M. H. 609 672 Stora, R. 241 242 663 Stoyanov, D. Tz 341 342 353 577 672 Strathdee, J. 242 576 655 672 Streater, R. F. xvii 240 327 349 350 351 374 378 445 464 467 512 534 575 577 611 619 631 648 672 682 Strocchi, F. 562 577 642 Strong interactions 2 127Ч128 151Ч152 405Ч406 496 562 Strong topology (see УConvergence strongФ) Structure constants 222Ч226 230Ч233 Stueckelberg, E. C. G. 465 672 673 SU(2) (special unitary group) 134 144 155Ч156 213 216 224 SU(2) (special unitary group), isospin and 127Ч128 405 SU(2) (special unitary group), representations 156 158 340Ч341 550 SU(2, 2) 172 SU(N) 211 Subgroup 210 Sudarshan, E. C. G. 8 127 150 351 405 545 546 575 576 630 634 640 653 673 Sukhanov, A. D. 460 466 662 673 Summation convention 129 Superconductivity 577 Superposition principle 126 Superselection rule(s) 122Ч128 142 240 250Ч251 326 379 534 535 537 596 599 601 Superselection rule(s), charge 206Ч207 251 312 Superselection rule(s), noncommutative 127Ч128 Superselection rule(s), univalence (spin) 122 250Ч251 379 534 Superselection rules and 122 127Ч128 379 Support 23 Support of analytic functional 466 Support of distribution 49 424Ч428 Sushko, N. V. 577 673 679 Swieca, J. A. 259 380 573 650 Symanzik, K. 381 401 464 467 468 658 659 673 Symmetric operator (see УLinear operator symmetricФ) Symmetries 352 577 Symmetries of physical world 131 404Ч405 498Ч499 Symmetries unitary operators and 36 242 475 562Ч563 577 УRelativistic УIsotopic Symmetries, broken 475 562Ч563 Symmetrization operator 197 Symplectic group 568Ч569 T-matrix 436 496Ч497 T-product (see УTime-ordered productФ) Tachyons 150 Tagamlitsky, Ya 106 673 Takahashi, Y. 576 655 Taylor series, as generalized function 425 Taylor, J. G. 467 638 576 643 TCP and spin-statistics not implied 610Ч611 TCP operator 298Ч299 322 474 498Ч504 511 514-519 TCP operator and 504 (see also УLorentz groupФ УRelativistic TCP operator in homogeneous distribution formalism 345 502 TCP theorem (TCP invariance) 4 337 474 476 498Ч504 512Ч518 538 574-575 TCP theorem (TCP invariance) for parafields 545Ч547 TCP theorem (TCP invariance), asymptotic states and 379 TCP theorem (TCP invariance), experimental verification 517 575 TCP theorem (TCP invariance), infinite-component counterexamples 567Ч573 578 610Ч611 TCP theorem (TCP invariance), scattering amplitudes and 436 514Ч517 TCP theorem (TCP invariance), spectral condition and 151 TCP theorem (TCP invariance), spin-statistics theorem and 513 538 572Ч575 TCP transformation of 498Ч504 Tempered distributions (S*) 11Ч12 27 33 40 46Ч48 55Ч56 58 60Ч65 73 85 105Ч106 422-423(see Tempered distributions (S*), analytic functions and 106 Tempered distributions (S*), field matrix elements as 249 422Ч423 Tempered distributions (S*), Fourier transforms 48 68Ч69 Tempered distributions (S*), radiation operators and 412Ч413 423 Tempered distributions (S*), terminological convention 48 Tempered growth (see УPolynomial growthФ) Tempered sequences (Sf) 120 Tensor 122 247Ч250 344 Tensor field 250 252 264 270 499 501 527 Tensor product 196Ч197 206Ч207 Tensor, analytic function 481Ч486 492 Tensor, antisymmetric 342 Tensor, traceless symmetric 339Ч340 Tensor, under SL(2) (see УSL(2) representationsФ) Test functions, space of (see У Test functions, vector, tensor 248 261Ч262 Theta function 56Ч57 69 100Ч102 383 447Ч448 453 456 461 Theta function 460Ч463 Theta function 392Ч394 Thirring, W., xviii 8 625 629 6 74 Three-particle space 152 204Ч205 Time reversal 110 164Ч165 177Ч178 180 191Ч192 241 320 322 323 Time reversal in homogeneous distribution formalism 343 Time reversal, charge conjugate spinor and 179 Time reversal, invariant distributions and 84Ч88 Time reversal, violation 498Ч499 (see also УDiscrete transformationsФ) Time-ordered product 3Ч4 359 382Ч383 396 464 Time-ordered product of currents 416Ч417 Time-ordered product, nomal product and 422 Time-ordered product, smeared 393Ч399 Time-ordered product, Wick 422 Timelike separation, notation 414 Titchmarsh, E. C. 523 632 Todorov, I. T., xvii 149 240 339 340 341 347 348 349 353 459 466 572 577 578 631Ч632 654 659 664 665 672 674 Toll, J. S. 510 545 576 634 655 659 Tolmachev, V. V. 577 628 Topological (continuous) group 212Ч214 242 Topology, topological space 18 22 24 25 28Ч29 212 586 598 Trace class 593 595 Trace of 173 Trace of Pauli matrix products 134 Transformation law, of fields (see УCovariance of Transition probabilities (see УProbabilityФ) Translation invariance 150 157 283 300 419 508 562 613 618 Translation invariance of state in 598Ч599 Translation invariance of TVEV 275 Translation invariance of Wightman functions 263 266Ч267 Translations 211 241 405 599 Transpose (transposition) 130 Tree, field-theory 620 Trivial (improper) subgroup 210 Trivial subspace 217 Trotter product formula 615 Trotter, H. F. 615 674 Truncated vacuum expectation value (TVEV) 272Ч281 374Ч378 386-388 Truncated vacuum expectation value (TVEV) of free fields 310 Tube 91 267 429 433 439Ч440 473Ч474 476 481Ч495 504Ч510 574 Tube, extended ( 3 473Ч474 481Ч489 493 504Ч510 574 Tube, permuted, symmetrized 505Ч510 TVEV (see УTruncated vacuum expectation valueФ) Two-particle space 152 200Ч204 Two-point Function 269Ч270 284 286 337 363Ч364 532Ч533 553-554 Two-point function of free scalar field 99Ч100 309 334Ч336 363 Two-point function of free spinor field 318Ч319 335 Two-point function of generalized free field 330 Two-point function, covariant structure, and homogeneous distributions 345Ч349 Uhlmann, A. 241 352 658 674 Ultraviolet divergences 360Ч361 383 455 456 468 556 612 620 Umezawa, H. 242 352 466 543 632 655 Unbounded operator (see УLinear operatorФ УDomain of УAlgebra of Unimodular group (see SL(2)) Unit element 209 585 596 Unitarity, of SЧmatrix 2 407 411 417 428 515 Unitary operator (see УLinear operator unitaryФ) Units, choice of 7 Univalence (see УSuperselection rule univalenceФ) Universal covering group (see УCovering groupФ) Universal enveloping algebra 147 223 Uretsky, J. L. 465 667 V Ч A current 500Ч501 VACUUM 111 151Ч152 193 248 256 296 351 362 406 407 599 608 609 619 Vacuum energy 619 Vacuum expectation value (vev) 260 274 281 318 351 Vacuum expectation value (VEV) of commutator 330Ч331 Vacuum expectation value (VEV) of current 441Ч442 Vacuum expectation value (VEV) of parafields 546Ч547 Vacuum expectation value (VEV) of radiation operator 412Ч413 Vacuum expectation value (VEV) of T-product 382Ч383 395Ч396 464 Vacuum expectation value (VEV), TCP transformation of 503Ч504 Vacuum in HaagТs theorem 550Ч551 555 560- 561 613 Vacuum polarization 561 Vacuum, anisotropy of 508 Vacuum, not annihilated by local field 530Ч531 Vacuum, space reflection and 324Ч325 Vacuum, uniqueness 151 257 272 276 283 292Ч294 297Ч301 351 618 619 Variation, bounded and total 20 Variational derivative (see УFunctional derivativeФ) Vector field 250 423 561 Vector mesons 406 Vector potential 382 Vector space 13Ч14 584 Vector space, countably normed 21Ч29 105 115 Vector space, locally convex 598 Vector space, normed 13Ч21 105 УNuclear Vectors, notation 7 77 Vectors, representation of SL(2) 341Ч342 344 Vectors, state (see УStatesФ) Velocity-space nonoverlap condition 384Ч389 396Ч399 Vertex part 562 VEV (see УVacuum expectation valueФ) Vilenkin, N. Ya 31 32 42 105 106 269 339 340 353 577 628 629 Visconti, A. 242 352 632 Vladimirov, V. S. 75 96 106 332 353 429 445 467 508 509 574 575 632 637 675 Volkov, D. V. 576 675 Volume element, spherical coordinates 80 von Neumann algebra 4 582 584 587Ч 589 602Ч611 624 Von Neumann Ч Pontryagin Ч Montgomery theorem 214Ч215 von Neumann, J. 37 240 558 630 675 von NeumannТs theorem 558Ч559 w (see УPauli Ч Lubanski Ч Bargmann vectorФ) W (invariant of Poincare group) 148 150 156 Watson, K. M. 8 629 Wave equation of field 337 Wave equation of field, first-order scalar 576 Wave equation of field, fundamental solution 77Ч82 Wave equation of field, higher spin 241Ч242 Wave function 336 Wave operators 422 556 Weak commutativity 257 299 Weak equivalence 595 Weak interactions 500Ч501 562 Weak local commutativity (WLC) 474 510Ч513 517Ч521 546Ч547 575 Weak topology, see Convergence, weak Weyl relations 559 569 Weidlich, W. 577 675 Weinberg, S. 242 352 468 642 675 Wentzel, G. 250 549 576 632 Westwater, M. J. 468 675 Wick ordering, see Normal product Wick polynomial 522Ч524 608Ч609 Wick, G. C. 205 240 242 327 652 658 675 676 WickТs theorem 422 Wiener, N. 427 631 Wightman approach 3 243Ч301 350Ч353 362Ч363 399 575 582 607 Wightman functional 287Ч301 Wightman functions 246 260Ч286 287 291Ч292 351Ч352 464 487 562 Wightman functions and 265Ч268 Wightman functions in HaagТs theorem 552Ч554 Wightman functions of free fields 309Ч310 313 318Ч319 Wightman functions of infinite-component field 571 Wightman functions, analyticity 267Ч268 473 476 487 504Ч510 Wightman functions, charge conservation and 313 Wightman functions, gauge transformation and 311 Wightman functions, space-time inversion and 532Ч533 Wightman, A. S. xvii 3 134 162 165 195 204 205 240 241 242 260 276 283 327 332 350 351 352 445 467 481 489 492 510 512 534 552 561 574 575 576 577 605 606 609 624 625 631 644 650 653 655 676 677 682 Wigner, E. P. 138 140 156 158 162 195 240 241 242 479 576 632 635 664 676 677 678 WignerТs theorem 139 234Ч239 242 Williams, D. N. 486 574 663 Wilner, M. 468 639 668 Winogradzki, J. 241 678 Wizimirski, Z. 283 351 678 WLC (see УLocal commutativityФ) WLC and 510Ч512 Wray, J. G. 468 668 678 Wu, C. S. 575 658 Yaglom, A. M. 242 252 577 645 Yang Ч Feldman equations 358 382 383 390Ч392 415 417Ч419 464 Yang, C. N. 464 517 575 658 679 Yndurain, F. J. 539 576 644 Young patterns 526 Yukawa potential 281 Yukawa theory 453Ч463 620Ч623 626 Zaikov, R. P. 353 674 ZavТyalov, O. I. 577 673 679 Zhelobenko, D. P. 242 632 Zimmermann, W. 381 401 464 465 467 468 607 625 638 645 658 659 679 Zumino, B. 576 660 УAlmost everywhereФ 47
–еклама
 |
|
ќ проекте
|
|
ќ проекте



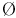 rmer, E.
rmer, E. Ф)
Ф)![$[\theta(x)]$](/math_tex/eb634063f6f5451939a34b82e444bf8d82.gif)
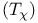
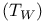
 -matrix products
-matrix products 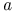
![$[S^{(\pm)}(x)]$](/math_tex/adf209656fa04e43e0b6586cc3425e0382.gif)