|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Klaas G., Leedham-Green C.R., Plesken W. — Linear Pro-p-Groups of Finite Width |
|
|
 |
| Предметный указатель |
"A and B" I.3.4
 (extension to products of the family (extension to products of the family  , by abuse of language) II.5.7 , by abuse of language) II.5.7
 , , 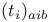 III.5.4 III.5.4
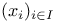 , ,  R.2.14 R.2.14
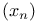 , , 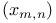 (m,n natural integers) R.7.8 (m,n natural integers) R.7.8
 , , 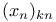 , , 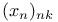 , , 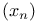 III.6.1 III.6.1
 , ,  I.4.1 I.4.1
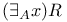 , , 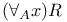 I.4.4 I.4.4
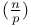 (n,p integers) III.5.8 (n,p integers) III.5.8
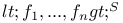 (S an echelon construction scheme, (S an echelon construction scheme, 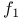 ,..., ,...,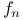 mappings) IV.1.1 mappings) IV.1.1
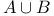 , ,  , , 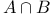 , , 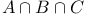 II.4.5 II.4.5
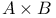 , , 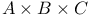 , , 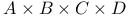 , (x,y,z) II.2.2 , (x,y,z) II.2.2
 , BA, , BA, 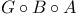 , CBA (A a subset of , CBA (A a subset of  , B a subset of , B a subset of 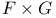 , C a subset of , C a subset of 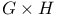 ) R.3.10 ) R.3.10
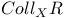 , , 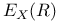 II.1.4 II.1.4
 (E,F sets) R.3.1 (E,F sets) R.3.1
 R.3.12 R.3.12
 (E,I sets) R.4.9 (E,I sets) R.4.9
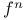 (f a mapping} III.6.2 (f a mapping} III.6.2
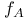 (f a mapping) R.2.13 (f a mapping) R.2.13
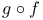 , , 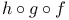 (f,g,h mappings) R.2.11 (f,g,h mappings) R.2.11
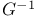 (G a graph), (G a graph), 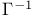 ( (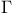 a correspondence) II.3.2 a correspondence) II.3.2
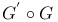 , , 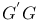 (G, (G, 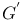 graphs), graphs), 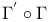 , , 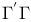 ( (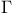 , , 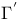 correspondences) II.3.3 correspondences) II.3.3
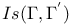 , Ord(E), , Ord(E), 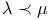 , ,  , , 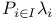 , ,  , ,  , , 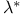 ( (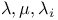 orde types) III.2 Exercise orde types) III.2 Exercise
 R.3.12 R.3.12
 , , 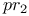 II.3.6 R.3.1 II.3.6 R.3.1
 , , 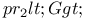 , , 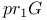 , , 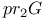 (G a graph) II.3.1 (G a graph) II.3.1
 II.5.4 II.5.4
 , , 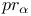 R.4.11 R.4.11
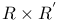 (R, (R, 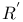 equivalence relations) II.6.8 equivalence relations) II.6.8
 (R,S equivalence relations) R.5.10 (R,S equivalence relations) R.5.10
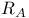 (R an equivalence relation, A a set) II.6.6 (R an equivalence relation, A a set) II.6.6
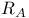 (R an equivalence relation, A a subset) R.5.5 (R an equivalence relation, A a subset) R.5.5
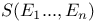 (S an echelon construction scheme, (S an echelon construction scheme, 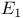 ,..., ,...,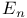 sets) IV.1.1 sets) IV.1.1
 , ,  III.1.9 III.1.9
 , sup X, , sup X,  , inf X R.6.7 , inf X R.6.7
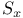 III.2.1 III.2.1
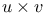 (u, v functions), (u, v) (by abuse of language) II.3.9 (u, v functions), (u, v) (by abuse of language) II.3.9
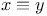 (mod R) (R an equivalence relation) II.6.1 (mod R) (R an equivalence relation) II.6.1
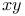 , , 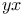 , ,  III.1.3 III.1.3
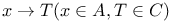 , , 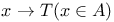 , , 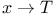 , , 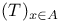 , T (by abuse language) (T a term) II.3.6 , T (by abuse language) (T a term) II.3.6
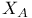 (X a subset) R.1.16 (X a subset) R.1.16
![$[\leftarrow,a]$](/math_tex/55055b14ebe4de7d862ed3873b33525182.gif) , , ![$]\leftarrow,a[$](/math_tex/61b47f5c95a7ea7f08ff35e888ff2e8b82.gif) , , ![$]a,\rightarrow[$](/math_tex/74d88b5466814294adbdf942f8fe3ed782.gif) , , 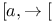 III.1.13 III.1.13
 , ,  , ,  R.4.9 R.4.9
 , ,  II.4.1 II.4.1
 , ,  , ,  R.4.4 R.4.4
 , ,  II.4.1 II.4.1
 , , 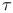 , , 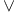 , ,  , ,  I.1.1 I.1.1
 , E — A R.1.7 , E — A R.1.7
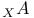 , X — A, , X — A,  , ,  II.1.7 II.1.7
 , ,  R.1.13 R.1.13
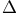 R.3.4 R.3.4
 , , 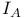 (A a set) II.3.3 (A a set) II.3.3
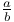 , a/b (a, b integers such that b divides a) III.5.6 , a/b (a, b integers such that b divides a) III.5.6
 , (T,U), , (T,U), 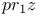 , , 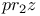 II.2.1 II.2.1
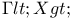 , , 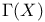 , , 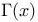 ( (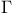 a correspondence, X a set, x an object) II.3.1 a correspondence, X a set, x an object) II.3.1
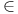 , , 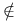 R.1.7 R.1.7
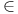 , , 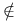 , , 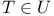 , , 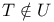 II.1.1 II.1.1
 , ,  , <, > R.6.3 , <, > R.6.3
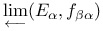 , ,  , ,  R.6.14 R.6.14
 ( (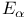 sets) III.7.1 sets) III.7.1
 ( (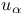 mappings) III.7.2 mappings) III.7.2
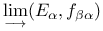 , ,  , ,  R.6.13 R.6.13
 ( (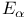 sets) III.7.5 sets) III.7.5
 ( (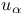 mappings) III.7.6 mappings) III.7.6
![$\lim\limits_{\xleftarrow[\alpha,\lambda]{}}E^{\lambda}_{\alpha}$](/math_tex/513c00a41aef17faff321310a8a8892e82.gif) , , ![$\lim\limits_{\xleftarrow[\alpha]{}}E^{\lambda}_{\alpha}$](/math_tex/5a99ee6460e15aefce79a3ed34771ec382.gif) , , ![$\lim\limits_{\xleftarrow[\alpha,\lambda]{}}u^{\lambda}_{\alpha}$](/math_tex/0dbaa81db7fc284d873548fa7de5059882.gif) , , ![$\lim\limits_{\xleftarrow[\alpha]{}}u^{\lambda}_{\alpha}$](/math_tex/448fed26cb60cf2b3773e1384c49fdee82.gif) III.7.3 III.7.3
![$\lim\limits_{\xrightarrow[\alpha,\lambda]{}}E^{\lambda}_{\alpha}$](/math_tex/cd7b9eaeac50042df3f4ee980c15ed6782.gif) , , ![$\lim\limits_{\xrightarrow[\alpha]{}}E^{\lambda}_{\alpha}$](/math_tex/1f84ecc939bae4d2173a4e5ba8c98f5d82.gif) , , ![$\lim\limits_{\xrightarrow[\alpha,\lambda]{}}u^{\lambda}_{\alpha}$](/math_tex/b4f909cf7ad01c59d44b372cb4d225c882.gif) , , ![$\lim\limits_{\xrightarrow[\alpha]{}}u^{\lambda}_{\alpha}$](/math_tex/25f5dae47df8af5775c98e2a96ce3a7082.gif) III.7.7 III.7.7
 , ,  I.3.5 I.3.5
 , , 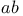 ( ( cardinals) III.3.3 cardinals) III.3.3
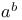 ( ( cardinals) III.3.5 cardinals) III.3.5
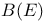 R.1.10 R.1.10
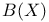 II.5.1 II.5.1
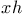 ( ( , , 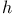 cardinals) III.3.2 cardinals) III.3.2
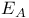 ( (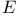 a set of subsets) R.1.16 a set of subsets) R.1.16
 , , 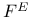 II.5.2 II.5.2
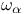 , , 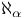 ( ( an ordinal) III.6 Exercise an ordinal) III.6 Exercise
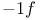 (f a mapping) R.2.6 (f a mapping) R.2.6
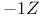 (Z a subset of a product) R.3.4 (Z a subset of a product) R.3.4
 , , 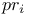 II.5.3 II.5.3
 , ,  R.4.9 R.4.9
 , , 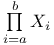 III.5.4 III.5.4
 , ,  III.6.1 III.6.1
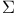 -admissible IV.3.2 -admissible IV.3.2
 -morphism IV.2.1 -morphism IV.2.1
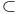 , , 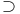 , , 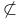 , ,  R.1.12 R.1.12
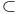 , , 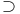 , , 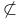 , ,  , , 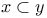 , , 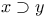 II.1.2 II.1.2
 , , 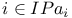 , ,  ( ( a family of cardinals) III.3.3 a family of cardinals) III.3.3
 (ordinal sum) III.1 Exercise (ordinal sum) III.1 Exercise
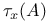 , (B|x)A, A{x}, A{x,y}, A{B}, A{B,C} I.1.1 , (B|x)A, A{x}, A{x,y}, A{B}, A{B,C} I.1.1
 ( ( a family of cardinals) III.3.2 a family of cardinals) III.3.2
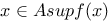 , ,  III.1.9 R.6.7 III.1.9 R.6.7
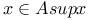 , , 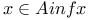 III.1.9 III.1.9
 R.1.8 R.1.8
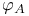 (A a subset of a set E) III.5.5 (A a subset of a set E) III.5.5
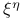 ( (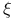 , , 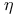 ordinals) III.2 Exercise ordinals) III.2 Exercise
(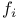 ) ( ) (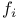 mappings) R.4.13 mappings) R.4.13
(f,g,h) (f,g,h mappings) R.3.12
(x,y) R.3.1
(x,y,z) R.3.12
0, 1, 2 III.3.1
3, 4 III.4.1
5, 6, 7, 8, 9 III.5.7
=, 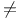 R.1.6 R.1.6
=, 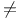 , T=U, , T=U, 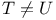 I.5.1 I.5.1
a — b (a,b integers, b<a) III.5.2
Adjunction (of one set to another) R.5.4
Adjunction of a greatest element to an ordered set III.1.7
Agreeing on a set (functions) II.3.5
Agreement (of two functions on a set) R.2.14
Aleph III.6.Ex.10
Antecedent assemblies I.App.4
Antidirected (ordered set) III.1.Ex.23
Applying the results of one theory in another I.2.4
Argument R.1.2
assembly I.1.1
Assembly of the first (second) species I.1.3
Assembly, antecedent I.App.4
Assembly, balanced I.App.4
Assembly, perfectly balanced I.App.4
Associated equivalence relation II.6.2
Associativity criterion for product structures IV.2.4
Associativity criterion of the intersection of a family of sets R.4.8
Associativity criterion of the product of a family of sets R.4.11
Associativity criterion of the union and intersection of two sets R.1.14
Associativity criterion of the union of a family of sets R.4.3
Automorphism IV.1.5 R.8.6
Auxiliary base sets IV.1.3 IV.1.4
Auxiliary constant, method of I.3.3
Auxiliary hypothesis, method of I.3.3
Axiom of Choice R.4.10
Axiom of extent II.1.3
Axiom of infinity III.6.1
Axiom of the ordered pair II.2.1
Axiom of the set of subsets II.5.1
Axiom of the set of two elements II.1.5
Axiom(s) of a species of structures IV.1.4
Axiom, explicit I.2.1
Axiom, implicit I.2.1
Axioms of structures of the same species R.8.2
Axioms, equivalent R.8.4
Balanced assembly I.App.4
Balanced word I.App.2
Base of a scale of sets R.8.1
Base of an expansion, or of a system of numeration III.5.7
Base sets (of an echelon construction} IV.1.1
Base sets, auxiliary IV.1.3 1.4
Base sets, principal IV.1.3 1.4
Bijection II.3.7 R.2.9
Bijective mapping II.3.7 R.2.9
Binomial coefficient III.5.8
Boolean lattice III.1.Ex.17
| Bound, greatest lower and least upper (of a setora mapping) III.1.9 R.6
Bound, least upper (of a set of cardinals} III.3.2
Bound, lower III.1.8 R.6.7
Bound, strict upper III.2.4
Bound, upper III.1.8 R.6.7
Bounded, bounded above, bounded below (set or mapping) III.1.8 R.6
Branched (ordered set) III.1..Ex.24
Canonical decomposition of a function II.6.5 R.5.3
Canonical extension, of a correspondence to sets of subsets II.5.1
Canonical extension, of a family of functions to the product sets II.5.7
Canonical extension, of mappings IV.1.2
Canonical extension, of two functions to the product sets II.3.9
Canonical extension, signed IV.2..Ex.1
Canonical injection II.3.7
Canonical mapping IV.App.4
Canonical mapping into a direct limit of a direct limit obtained by restriction of the index set III.7.6
Canonical mapping of 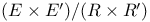 onto onto 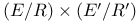 II.6.8 R.5.10 II.6.8 R.5.10
Canonical mapping of 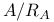 onto f<A> II.6.6 R.5.5 onto f<A> II.6.6 R.5.5
Canonical mapping of  onto onto 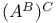 II.5.2 R.4.14 II.5.2 R.4.14
Canonical mapping of  onto onto 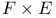 R.3.4 R.3.4
Canonical mapping of  onto onto 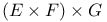 , etc. R.3.12 , etc. R.3.12
Canonical mapping of  into into  III.7.5 R.6.13 III.7.5 R.6.13
Canonical mapping of 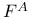 onto onto 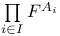 (where (where  , and , and 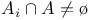 whenever whenever 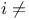 ) R.4.15 ) R.4.15
Canonical mapping of 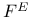 onto onto  II.5.2 II.5.2
Canonical mapping of  into into  III.7.1 R.6.14 III.7.1 R.6.14
Canonical mapping of 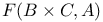 onto onto 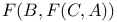 II.5.2 II.5.2
Canonical mapping of  onto onto  ( (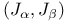 a partition of I) II.5.5 a partition of I) II.5.5
Canonical mapping of  onto onto  II.5.5 R.4.11 II.5.5 R.4.11
Canonical mapping of  onto onto  R.4.13 R.4.13
Canonical mapping of 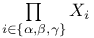 onto onto 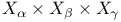 II.5.3 II.5.3
Canonical mapping of  onto onto 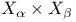 II.5.3 II.5.3
Canonical mapping of  onto onto 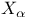 II.5.3 II.5.3
Canonical mapping of (E/S)/(R/S) onto E/R II.6.7 R.5.9
Canonical mapping of a subset of E into E II.3.7 R.2.3
Canonical mapping of an inverse limit into an inverse limit obtained by restriction of the index set III.7.1
Canonical mapping of E onto E/R II.6.2 R.5.2
Canonical mapping of G onto  (G a graph) II.3.7 (G a graph) II.3.7
Canonical mapping, symmetry R.3.4
Cantor's theorem III.3.6
Cardinal of a set III.3.1
Cardinal sum III.3.3
Cardinal, dominant III.6..Ex.21
Cardinal, finite III.4.1
Cardinal, inaccessible III.6..Ex.22
Cardinal, product III.3.3
Cardinal, regular III.6..Ex.17
Cardinal, singular III.6..Ex.17
Cardinal, strongly inaccessible III.6.Ex.22
Chain of an element in an ordered set (with respect to a mapping) III.2.Ex.6
Characteristic function of a subset of a set III.5.5
Characterization, typical IV.1.4
Choice, axiom of R.4.9
Class of objects equivalent to x (with respect to an equivalence relation) II.6.9
Class, equivalence II.6.2 R.5.2
Closed interval III.1.13 R.6.4
Closure (mapping of an ordered set into itself) III.1.Ex.13
Coarser equivalence relation II.6.7
Coarser equivalence relation, preordering III.1.4
Coarser equivalence relation, structure IV.2.2
Coefficient, binomial III.5.8
Cofinal subset III.1.7 R.6.5
Coincidence (of two functions on a set) II.3.5 R.2.14
Coinitial subset III.1.7 R.6.5
Collectivizing relation II.1.4
Commutativity (of union and intersection) R.1.14
Comparable elements III.1.12
Comparable structures IV.2.2
Compatibility, of a function with two equivalence relations II.6.5 R.5
Compatibility, of a relation with an equivalence relation II.6.5 R.5.7
Complement of a set II.1.7 R.1.7
Complete lattice III.1.Ex.11
Complete solution I.5.2
Completely ramified (ordered set) III.2.Ex.8
Completion of an ordered set III.1.Ex.15
Composition, of mappings R.2.11
Composition, of sets R.3.10
Composition, of two correspondences II.3.3
Composition, of two graphs II.3.3
Conjunction of two relations I.3.4
Connected components of a set with respect to a relation II.6.Ex.10
Constant of a theory I.2.1
Constant, auxiliary I.3.3
Constant, function or mapping II.3.4 R.2.3
Constituents of a set with respect to a relation II.6.Ex.11
Construction, echelon IV.1.1
Construction, formative I.1.3
Contained in a set II.1.2 R.1.12
Continuum Hypothesis III.6.4
Continuum, power of III.6.4
Contradictory axioms R.8.6
Contradictory theory I.2.2
Contravariant signed echelon type IV.2.Ex.1
Coordinate (first, second) of an ordered pair II.2.1
Coordinate function (first, second) II.3.6
Coordinate function of index i II.5.3
Coordinate functions, on a product of a family of sets R.4.11
Coordinate functions, on a product of several sets R.3.12
Coordinate functions, on a product of two sets R.3.1
Corollary I.2.2
Correspondence defined at an object x II.3.1
Correspondence denned by a relation II.3.1
Correspondence, between two sets II.3.1
Correspondence, inverse II.3.2
Correspondence, one-to-one II.3.7 R.2.9
Correspondences, composition of II.3.3
Countable set III.6.4 R.7.7
Countable union, intersection, product R.7.9
Covariant signed echelon type IV.2.Ex.1
Covering II.4.6 R.4.4
Covering of a set II.4.6
Covering, finer II.4.6
Criterion of deduction I.3.3
Criterion of substitution I.1.2
Criterion, deductive I.2.2
Criterion, formative I.1.4
Critical ordinal III.6.Ex.13
Decent set III.2.Ex.20
Decimal system III.5.7
Decomposition, canonical II.6.5 R.5.3
Decreasing family of subsets III.1.5 R.6.12
Decreasing mapping III.1.5 R.6.12
Deduced (structure) IV.1.6
Deduction, criterion of I.3.3
Deduction, procedure IV.1.6
Deductive criterion I.2.2
Definition I.1.1
Degree of disjointness of a covering III.6.Ex.25
Demonstrative text I.2.2
Descending induction III.4.3
Diagonal mapping, of A into  II.3.7 R.3.4 II.3.7 R.3.4
Diagonal mapping, of E into  II.5.3 II.5.3
Diagonal, of  II.3.3 R.3.4 II.3.3 R.3.4
Diagonal, of  II.5.3 II.5.3
Diagrams R.2.2
Difference of two integers III.5.2
Different from I.5.1
digit III.5.7
Direct image of a structure IV.2.6
Direct limit, of a direct system of mappings III.7.6 R.6.13
Direct limit, of a direct system of sets III.7.5 R.6.13
Direct system, of mappings III.7.6 R.6.13
Direct system, of sets III.7.5 R.6.13
Direct system, of subsets III.7.6
Directed (left, right) III.1.10 R.6.8
Directed with respect to the relation  III.1.10 III.1.10
Disjoint segments I.App.1
Disjoint sets II.4.7 R.1.13
Disjunction, of cases, method of I.3.3
Disjunction, of two relations I.1.3
Distributive lattice III.1.Ex.16
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 (extension to products of the family
(extension to products of the family  ,
, 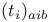
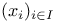 ,
, 
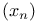 ,
, 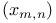 (m,n natural integers)
(m,n natural integers)  ,
, 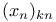 ,
, 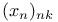 ,
,  ,
, 
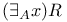 ,
, 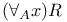
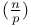 (n,p integers)
(n,p integers) 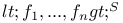 (S an echelon construction scheme,
(S an echelon construction scheme, 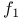 ,...,
,...,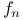 mappings)
mappings) 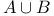 ,
,  ,
, 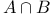 ,
, 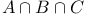
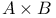 ,
, 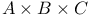 ,
, 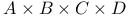 , (x,y,z)
, (x,y,z)  , BA,
, BA, 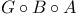 , CBA (A a subset of
, CBA (A a subset of  , B a subset of
, B a subset of 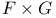 , C a subset of
, C a subset of 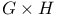 )
) 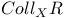 ,
, 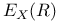

 (E,I sets)
(E,I sets) 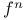 (f a mapping}
(f a mapping} 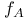 (f a mapping)
(f a mapping) 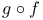 ,
, 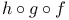 (f,g,h mappings)
(f,g,h mappings) 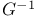 (G a graph),
(G a graph), 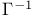 (
(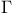 a correspondence)
a correspondence) 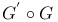 ,
, 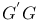 (G,
(G, 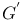 graphs),
graphs), 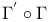 ,
, 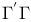 (
(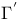 correspondences)
correspondences) 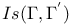 , Ord(E),
, Ord(E), 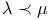 ,
,  ,
, 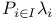 ,
,  ,
,  ,
, 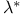 (
(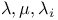 orde types)
orde types) 
 ,
, 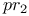
 ,
, 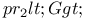 ,
, 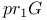 ,
, 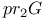 (G a graph)
(G a graph) 
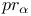
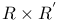 (R,
(R, 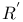 equivalence relations)
equivalence relations)  (R,S equivalence relations)
(R,S equivalence relations) 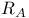 (R an equivalence relation, A a set)
(R an equivalence relation, A a set) 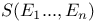 (S an echelon construction scheme,
(S an echelon construction scheme, 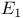 ,...,
,...,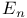 sets)
sets)  ,
, 
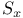
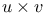 (u, v functions), (u, v) (by abuse of language)
(u, v functions), (u, v) (by abuse of language) 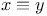 (mod R) (R an equivalence relation)
(mod R) (R an equivalence relation) 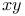 ,
, 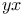 ,
, 
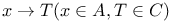 ,
, 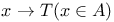 ,
, 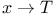 ,
, 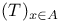 , T (by abuse language) (T a term)
, T (by abuse language) (T a term) 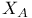 (X a subset)
(X a subset) ![$[\leftarrow,a]$](/math_tex/55055b14ebe4de7d862ed3873b33525182.gif) ,
, ![$]\leftarrow,a[$](/math_tex/61b47f5c95a7ea7f08ff35e888ff2e8b82.gif) ,
, ![$]a,\rightarrow[$](/math_tex/74d88b5466814294adbdf942f8fe3ed782.gif) ,
, 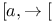
 ,
,  ,
, 
 ,
,  ,
, 
 ,
, 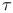 ,
, 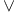 ,
,  ,
, 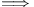
 , E — A
, E — A 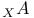 , X — A,
, X — A, 
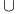 ,
, 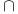
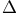
 ,
, 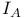 (A a set)
(A a set) 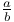 , a/b (a, b integers such that b divides a)
, a/b (a, b integers such that b divides a)  , (T,U),
, (T,U), 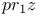 ,
, 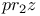
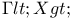 ,
, 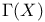 ,
, 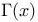 (
(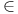 ,
, 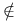
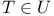 ,
, 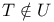
 ,
,  , <, >
, <, > 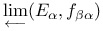 ,
,  ,
, 
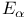 sets)
sets) 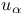 mappings)
mappings) 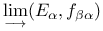 ,
,  ,
, 
![$\lim\limits_{\xleftarrow[\alpha,\lambda]{}}E^{\lambda}_{\alpha}$](/math_tex/513c00a41aef17faff321310a8a8892e82.gif) ,
, ![$\lim\limits_{\xleftarrow[\alpha]{}}E^{\lambda}_{\alpha}$](/math_tex/5a99ee6460e15aefce79a3ed34771ec382.gif) ,
, ![$\lim\limits_{\xleftarrow[\alpha,\lambda]{}}u^{\lambda}_{\alpha}$](/math_tex/0dbaa81db7fc284d873548fa7de5059882.gif) ,
, ![$\lim\limits_{\xleftarrow[\alpha]{}}u^{\lambda}_{\alpha}$](/math_tex/448fed26cb60cf2b3773e1384c49fdee82.gif)
![$\lim\limits_{\xrightarrow[\alpha,\lambda]{}}E^{\lambda}_{\alpha}$](/math_tex/cd7b9eaeac50042df3f4ee980c15ed6782.gif) ,
, ![$\lim\limits_{\xrightarrow[\alpha]{}}E^{\lambda}_{\alpha}$](/math_tex/1f84ecc939bae4d2173a4e5ba8c98f5d82.gif) ,
, ![$\lim\limits_{\xrightarrow[\alpha,\lambda]{}}u^{\lambda}_{\alpha}$](/math_tex/b4f909cf7ad01c59d44b372cb4d225c882.gif) ,
, ![$\lim\limits_{\xrightarrow[\alpha]{}}u^{\lambda}_{\alpha}$](/math_tex/25f5dae47df8af5775c98e2a96ce3a7082.gif)
 ,
, 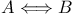
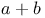 ,
, 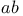 (
( cardinals)
cardinals) 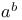 (
(
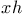 (
( ,
, 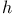 cardinals)
cardinals) 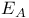 (
(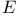 a set of subsets)
a set of subsets)  ,
, 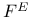
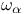 ,
, 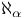 (
( an ordinal)
an ordinal) 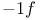 (f a mapping)
(f a mapping) 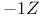 (Z a subset of a product)
(Z a subset of a product)  ,
, 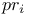

 ,
, 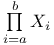
 ,
, 
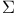 -admissible
-admissible  -morphism
-morphism 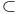 ,
, 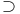 ,
, 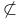 ,
, 
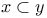 ,
, 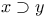
 ,
, 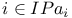 ,
,  (
( a family of cardinals)
a family of cardinals)  (ordinal sum)
(ordinal sum) 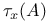 , (B|x)A, A{x}, A{x,y}, A{B}, A{B,C}
, (B|x)A, A{x}, A{x,y}, A{B}, A{B,C}  (
(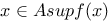 ,
, 
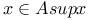 ,
, 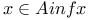
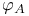 (A a subset of a set E)
(A a subset of a set E) 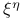 (
(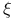 ,
, 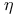 ordinals)
ordinals) 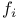 ) (
) (
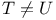
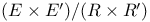 onto
onto 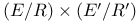
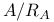 onto f<A>
onto f<A>  onto
onto 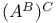
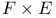
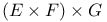 , etc.
, etc.  into
into 
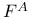 onto
onto 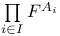 (where
(where  , and
, and 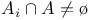 whenever
whenever 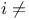 )
)  into
into 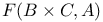 onto
onto 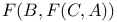
 (
(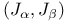 a partition of I)
a partition of I) 
 onto
onto 
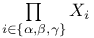 onto
onto 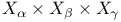
 onto
onto 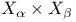
 onto
onto 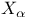
 (G a graph)
(G a graph) 