|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Klaas G., Leedham-Green C.R., Plesken W. — Linear Pro-p-Groups of Finite Width |
|
|
 |
| Предметный указатель |
Subsequence (of a sequence) III.6.1 R.8.7
Subset of a set II.2.1 R.1.7
Subset, cofinal III.1.7 R.6.5
Subset, coinitial III.1.7 R.6.5
Subset, consisting of a alone R.1.9
Subset, empty R.1.8
Subset, saturated (with respect to an equivalence relation) II.6.4
Subset, symmetric R.3.4
Subsets, disjoint R.1.13
Subsets, set of II.5.1 R.1.10
Subsets, stable R.2.5
Substantific sign I.1.3
Substitution, criterion of I.1.2
Sum of a family of sets II.4.8
Sum of cardinals III.3.3
Sum of powers R.7.5
Sum of sets R.4.5
Sum, cardinal III.3.3
Sum, ordinal III.2.Ex.13
sup X, inf X III.1.9
sup(x,y), inf(x,y) III.1.9
Supremum III.1.9 R.6.7
Surjection II.3.7 R.2.4
Surjective mapping II.3.7 R.2.4
Symbol, functional I.5.3
Symbol, numerical III.5.7
Symmetric graph II.2.3
Symmetric relation or subset II.6.1 R.3.4
Symmetry, canonical R.3.4
System of numeration III.5.7
System of representatives II.6.2
System, decimal III.5.7
System, direct III.7.5 R.6.13
System, dyadic III.5.7
System, inverse III.7.1 R.6.14
T/R (T, R equivalence relations) R.5.9
Target of a correspondence II.3.1
Term I.1.3
Term, (first, kth, last) of a finite sequence III.5.4
Term, general R.7.8
Term, intrinsic IV.1.6
Term, nth R.7.8
Term, satisfying a relation I.2.2
Term, which can be put in the form T I.5.2
Text, demonstrative I.2.2
Theorem I.2.2
Theorem of Cantor III.3.6
Theorem of legitimation I.3.3
Theorem of Zermelo III.2.3 R.6.5
Theories, equivalent I.2.4
Theory I.1.1 I.2.1 I.2.2
Theory multivalent R.3.7
Theory of a species of structures IV.1.4
Theory of sets II.1.1
Theory of structures of a given species R.8.2
Theory quantified I.4.2
Theory stronger I.2.4
Theory univalent R.8.7
Theory, contradictory I.2.2
| Theory, equalitarian I.5.1
Theory, logical I.3.1
Total order relation, total ordering III.1.12
Totally ordered set III.1.12 R.6.4
Trace of a family of sets II.4.5
Trace of a subset, or set of subsets R.1.16
Transform of an element by a function II.3.4 R.2.4
Transitive relation II.6.1 R.5.1
Transitive set III.2.Ex.20
Transitivity criteria IV.2.3 IV.2.5
Transport of structure R.8.5
Transportable relation IV.1.3
Transporting a structure IV.1.5
Transversal II.6.2
Triple II.2.2
Triple sequence III.6.1
True relation I.2.2
Typical characterization of a species of structures IV.1.4
Typical quantifier I.4.4
Typification IV.1.3
Unbounded interval III.1.13 R.6.4
Underlying structure IV.1.6
Union of a family of sets R.4.2
Union of a set of sets II.4.1
Union of several sets R.1.13
Union, countable R.7.9
Univalent species of structures IV.1.5
Univalent theory R.8.7
Universal mapping IV.3.1
Universal problem IV.3.1
Universal quantifier I.4.1
Universal set IV.3.1
Upper bound III.1.8 R.6.7
Upper bound, least III.1.9 R.6.7
Upper bound, strict III.2.4
Value, of a function II.3.4
Value, of a function at an element R.2.1
Value, of a variable R.1.2
Value, taken by a correspondence II.3.1
Variable R.1.2
Variance of an assembly IV.2.Ex.1
Weak compatibility (of an equivalence relation with a preorder relation) III.1.Ex.2
Weight of a sign I.1.3 I.App.1
Well-ordered set III.2.1 R.6.5
Well-ordering, well-ordering relation III.2.1
Without gaps (ordered set) III.1.Ex.19
Word I.App.1
Word, balanced I.App.3
Word, empty I.App.1
Word, significant I.App.2
x<y, y<x III.1.3
Zermelo's axiom (=axiom of choice) R.4.9
Zermelo's theorem III.2.3 R.6.5
Zorn's lemma III.2.4 R.6.10
[a, b], [a,b[, ]a, b], ]a, b[, ![$]\leftarrow, a]$](/math_tex/d3f6f081a84aaefed1a728c5f6ba6d9882.gif) , , ![$]\leftarrow, a[$](/math_tex/735a8809a839cc8b056d58a4f2f66bb382.gif) , , 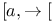 , , ![$]a, \rightarrow[$](/math_tex/05cf01eb7a3474d4f62ffdee3c012a3582.gif) , , ![$]\leftarrow,\rightarrow[$](/math_tex/4f2aba72173a099b9616c08204d8b55482.gif) R.6.4 R.6.4
[a,b], [a,b[, ]a,b], ]a,b[ III.1.13
{a} R.1.9
{x,y,z} II.4.5 R.1.13
{x,y}, {x} II.1.5
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$]\leftarrow, a]$](/math_tex/d3f6f081a84aaefed1a728c5f6ba6d9882.gif) ,
, ![$]\leftarrow, a[$](/math_tex/735a8809a839cc8b056d58a4f2f66bb382.gif) ,
, 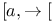 ,
, ![$]a, \rightarrow[$](/math_tex/05cf01eb7a3474d4f62ffdee3c012a3582.gif) ,
, ![$]\leftarrow,\rightarrow[$](/math_tex/4f2aba72173a099b9616c08204d8b55482.gif)