|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Klaas G., Leedham-Green C.R., Plesken W. — Linear Pro-p-Groups of Finite Width |
|
|
 |
| Предметный указатель |
Multiple sequence III.6.1
Multivalent theory R.8.7
Mutually disjoint (family of sets) II.4.7
N R.6.2
n! (n an integer) III.5.8
N, 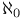 III.6.1 III.6.1
Natural integer III.4.1
Negation of a relation I.1.3
Noetherian induction, principle of III.6.5
Noetherian set III.6.5
not (A), (A) or (B),  I.2 I.2
nth iterate of a mapping III.6.2 R.2.11
nth term of a sequence III.6.1 R.7.8
Number of elements of a finite set III.4.1
Numeration, system of III.5.7
Numerical symbol III.5.7
Odd integer III.5.6
One-to-one correspondence, mapping II.3.7 R.2.9
Open interval III.1.13 R.6.4
Opposite order relation, preorder relation III.1.1 III.1.2 R.6.1
Order relation between x and y, with respect to x and y III.1.1
Order relation on a set III.1.1 R.6.1
Order relation, associated with a preorder relation III.1.2
Order relation, induced on a set III.1.4
Order relation, lexicographical III.2.6
Order relation, opposite to an order relation III.1.1
Order type III.2.Ex.13
Order-preserving mapping III.1.5
Order-reversing mapping III.1.5
Order-structure R.6.1
Order-structure, total III.1.12
Ordered pair II.2.1
Ordered set III.1.3 R.6.1
Ordered set, antidirected III.1.Ex.23
Ordered set, branched III.1.Ex.24
Ordered set, completely ramified III.2.Ex.8
Ordered set, partially well-ordered III.2.Ex.4
Ordered set, ramified III.2.Ex.8
Ordered set, scattered III.1.Ex.20
Ordered set, without gaps III.1.Ex.19
Ordering III.1.1 R.6.1
Ordering, induced III.1.4
Ordering, lexicographical III.2.6
Ordering, product III.1.4
Ordering, total III.1.12
Ordinal IlI.2.Ex.14
Ordinal product (of order-types) III.2.Ex.13
Ordinal product (of order-types), regular III.6.Ex.16
Ordinal product (of order-types), singular III.6.Ex.16
Ordinal sum (of order-types) III.2.Ex.13
Ordinal sum, of a family of non-empty ordered sets indexed by a ordered set III.1.Ex.3
Ordinal, critical III.6.Ex.13
Ordinal, functional symbol III.2.Ex. 17
Ordinal, inaccessible initial III.6.Ex.16
Ordinal, indecomposable III.2.Ex.16
Ordinal, initial III.6.Ex.10
Pair, ordered II.2.1
Pairwise disjoint (family of subsets) R.4.4
Parameter, parametric set, parametric representation II.3.7 R.2.14
Partial mapping II.3.9 R.3.13
Partial product II.5.4
Partially well-ordered (ordered set) III.2.Ex.1
Partition of a set II.4.7 R.4.4
Passage to quotient sets II.6.3 II.6.5 R.5.7 R.5.8
Perfectly balanced assembly I.App.4
Permutation II.3.7 R.2.9
Poorer (species of structures) IV.1.6
Power, of a set III.3.1 R.7.2
Power, of the continuum III.6.4
Powers, equivalent R.7.2
Powers, sum of R.7.5
Predecessor (of an ordinal) III.2.Ex.14
Preorder relation III.1.2 R.6.1
Preorder relation on a set III.1.2
Preorder relation, opposite to a preorder relation III.1.2
Preordered set R.6.1
Preordering III.1.2
Preordering (coarser, finer) III.1.4
Principal base sets IV.1.3 IV.1.4
Principle of Induction III.4.3
Principle of Noetherian induction III.6.5
Principle of transfinite induction III.2.2
Procedure of deduction of structures IV.1.6
Product cardinal III.3.3
Product of a family of mappings II.5.7
Product of a family of sets II.5.3 R.4.9
Product of cardinals III.3.3
Product of order relations, orderings, preorder relations, preorderings III.1.4
Product of ordered sets, preordered sets III.1.4
Product of several sets R.3.12
Product of two coverings II.4.6
Product of two equivalence relations II.6.8 R.5.10
Product of two sets II.2.2 R.3.1
Product ordinal III.2.Ex.13
Product partial II.5.4
Product structure, product of structures IV.2.4
Product, lexicographic III.2.6
Projection onto a factor II.5.3
Projection onto a partial product II.5.4
Projection, (first, second) of a graph II.3.1
Projection, (first, second) of an ordered pair II.2.1
Projections R.3.1 R.3.12 R.4.11
proof I.2.2
Proper segment I.App.1
Property of finite character III.4.5
Proposition I.2.2
Pseudo-ordinal III.2.Ex.20
Quantified theory I.4.2
Quantifier, existential I.4.1
Quantifier, typical I.4.4
Quantifier, universal I.4.1
Quotient equivalence relation II.6.7 R.5.9
Quotient of a preorder relation or preordered set by an equivalen relation III.1.Ex.2
Quotient of two integers III.5.6
Quotient set II.6.2 R.5.2
Quotient structure IV.2.6
R/S (R, S equivalence relations) II.6.7
Ramified (ordered set) III.2.Ex.8
Range, of a correspondence II.3.1
Range, of a graph II.3.1
Realization, of a signed echelon type IV.2.Ex.1
Realization, of an echelon type IV.1.Ex.1
Reductio ad absurdum, method of I.3.3
Refinement of a covering II.4.6
Reflexive relation on a set II.6.1 R.5.1
Regular cardinal III.6.Ex.17
Regular ordinal IV.6.Ex.16
Relation I.1.3
Relation between an element of A and an element of B II.3.1
Relation of equality I.5.1 R.1.6
Relation of inclusion II.1.2 III.1.1 R.1.12
Relation of membership II.1.1 R.1.10
Relation order III.1.1 R.6.1
Relation,  (resp. (resp.  ) III.1.3 ) III.1.3
Relation, collectivizing II.1.4
Relation, compatible with an equivalence relation II.6.3 R.5.7
Relation, compatible with two equivalence relations II.6.8
Relation, equivalence II.6.1 R.5.2
Relation, false I.2.2
Relation, functional I.5.3 R.2.1
Relation, having a graph II.3.1
Relation, induced by an equivalence relation on passing to the quotient II.6.3
Relation, preorder III.1.2 R.6.1
Relation, reflexive II.6.1 R.5.1
Relation, single-valued I.5.3
Relation, symmetric II.6.1 R.3.4
Relation, total order II.1.12
Relation, transitive II.6.1 R.5.1
Relation, transportable IV.1.3
Relation, true I.2.2
| Relation, well-ordering III.2.1
Relational sign I.1.3
Relations, equivalent I.3.5 R.1.3
Relative complement (of an element in a lattice) III.1.Ex.17
Relatively complemented lattice III.1.Ex.17
Remainder (on division of a by b) III.5.6
Representation, parametric II.3.7 R.2.14
Representative, of an equivalence class II.6.2
Representatives, system of II.6.2
Restricted Induction III.4.3
Restriction, of a direct system III.7.6
Restriction, of a function II.3.5 R.2.13
Restriction, of an inverse system III.7.1
Retraction of an injection II.3.8
Richer structure R.8.3
Right directed set III.1.10 R.6.8
Right inverse (of a surjection) II.3.8
Right-hand endpoint of an interval III.1.13
R{x,y,z} R.1.2
Saturated set R.5.6
Saturation of a set with respect to an equivalence relation R.5.6
Scale of sets R.8.1
Scattered (ordered set) III.1.Ex.20
Scheme I.2.1
Scheme of selection and union II.1.6
Scheme, echelon construction IV.1.1
Second coordinate of an ordered pair II.2.1
Second projection II.3.1
Second species I.1.3
Section, of a correspondence II.3.1
Section, of a graph II.3.1
Section, of a set (with respect to an equivalence relation) II.6.2
Section, of a subset of a product R.3.7
Section, of a surjection II.3.8
Segment of a word I.App.1
Segment of an assembly I.App.4
Segment with endpoint x III.2.1
Segment, final I.App.1
Segment, initial I.App.1
Segment, proper I.App.1
Segments, disjoint I.App.1
Selection and union, scheme of II.1.6
Separation (of the elements of E by  -mappings) IV.3.3 -mappings) IV.3.3
SEQUENCE R.7.8
Sequence of elements of a set III.6.1
Sequence, double R.7.8
Sequence, finite III.5.4 R.7.8
Sequence, infinite III.6.1 R.7.8
Sequence, obtained by ranging a countable family in an order defined by a maping III.6.1
Sequence, significant I.App.2
Sequence, stationary III.6.5
Sequence, triple, multiple III.6.1
Sequences differing only in the order of their terms III.6.1 R.7.8
Set II.1.1
Set of a-morphisms IV.2.1
Set of all 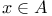 such that P II.1.6 such that P II.1.6
Set of all x such that R (R a relation collectivizing in x) II.1.4
Set of cardinals  III.3.2 III.3.2
Set of classes of equivalent objects II.5.9
Set of elements of a family II.3.4 R.2.14
Set of mappings of E into F II.5.2 R.2.2
Set of n elements (n an integer) III.4.1
Set of objects of the form T for 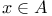 II.1.6 II.1.6
Set of parameters of parametric representation II.3
Set of subsets of a set II.5.1 R.1.10
Set of subsets, of finite character III.4.5
Set, base IV.1.3 IV.1.4
Set, bounded, bounded above, bounded below III.1.8 R.6.7
Set, consisting of a single element II.1.5
Set, countable III.6.4 R.7.7
Set, decent III.2.Ex.20
Set, directed III.1.10 R.6.8
Set, empty II.1.7 R.1.8
Set, endowed with a structure IV.1.4
Set, equipotent to another set R.7.1
Set, finite III.4.1
Set, index (of a family) II.3.4
Set, inductive III.2.4 R.6.9
Set, infinite III.6.1
Set, left directed III.1.10 R.6.8
Set, Noetherlan III.6.5
Set, ordered III.1.3 R.6.1
Set, preordered III.1.3 R.6.1
Set, product R.3.1 R.3.12.
Set, quotient II.6.2 R.5.2
Set, representative (of a relation) II.3.1
Set, right directed III.1.10 R.6.8
Set, totally ordered III.1.12 R.6.4
Set, transitive III.2..Ex.20
Set, universal IV.3.1
Set, well-ordered III.2.1 R.6.5
Set, whose only element is x II.1.5
Sets, composition of R.3.10
Sets, disjoint II.4.7
Sets, equipotent III.3.1
Sets, isomorphic IV.1.5
Sets, theory of II.1.1
SIGN I.1.1 I.App.1
Sign, logical I.1.1
Sign, rational I.1.3
Sign, specific I.1.1
Sign, substantific I.1.3
Signed canonical extension IV.2.Ex.1
Signed echelon type IV.2.Ex.1
Significant sequence, word I.App.2
Single-valued relation I.5.3
Singular cardinal III.6.Ex.17
Singular ordinal III.6.Ex.l6
Smaller than IV.1.3
Solution (of an equation) I.2.2
Solution of a universal mapping problem IV.3.1
Solution, complete (or general) I.5.2
Source of a correspondence II.3.1
Species of algebraic structures IV.1.4
Species of order structures IV.1.4
Species of structures IV.1.4 R.8.2
Species of topological structures IV.1.4
Species, equivalent IV.1.7
Species, poorer (richer) IV.1.6
Specific sign I.1.1
Stable subset R.2.5
Stationary sequence III.6.5
Strict upper bound III.2.4
Strictly coarser (finer) structure IV.2.2
Strictly decreasing (increasing) III.1.5 R.6.12
Strictly greater (less) III.1.3 R.6.3 R.7.3
Stronger theory I.2.4
Strongly inaccessible cardinal III.6.Ex.22
Structure of a set IV.1.4 R.8.2
Structure of species 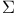 IV.1.4 IV.1.4
Structure, coarser IV.2.2
Structure, deduced IV.1.6
Structure, final IV.2.5
Structure, finer IV.2.2
Structure, generic IV.1.4
Structure, induced IV.2.4
Structure, initial IV.2.3
Structure, order R.6.1
Structure, product IV.2.4
Structure, quotient IV.2.6
Structure, richer R.8.2
Structure, strictly coarser (finer) IV.2.2
Structure, subordinate IV.1.6
Structure, transport of R.8.5
Structure, underlying IV.1.6
Structures, comparable IV.2.2
Structures, isomorphic IV.1.5 R.8.6
Subfamily II.3.5 R.2.14
Sublattice III.4.Ex.9
Subordinate structure IV.1.6
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



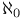

 (resp.
(resp.  )
)  -mappings)
-mappings) 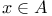 such that P
such that P