|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Klaas G., Leedham-Green C.R., Plesken W. — Linear Pro-p-Groups of Finite Width |
|
|
 |
| Предметный указатель |
Distributivity, of union and intersection of a family of sets R.4.3 R.4.8
Distributivity, of union and intersection of two sets R.1.14
Divergent mapping (of an ordinal into itself) III.6.Ex.23
Divisible by an integer III.5.6
Division of an integer III.5.6
Division, Euclidean III.5.6
Domain, of a correspondence II.3.1
Domain, of a graph II.3.1
Dominant cardinal III.6.Ex.21
Double family II.3.4
Double sequence III.6.1 R.7.8
Dual formulae R.1.15 R.4.7
Duality rule R.1.15 R.4.7
Dyadic system III.5.7
E/R (E a set, R an equivalence relation on E) R.5.2
E/R (E a set, R an equivalence relation) II.6.2
Echelon type IV.1.Ex.1
Echelon, echelon construction, echelon construction scheme IV.1.1
Echelon, signed IV.2.Ex.1
Element II.1.1
Element, fixed (under a mapping or set of mappings) R.2.3
Element, generic R.1.2
Element, greatest III.1.3 R.6.5
Element, invariant (under a mapping or set of mappings) R.2.3
Element, least III.1.3 R.6.5
Element, maximal III.1.6 R.6.6
Element, minimal III.1.6. R.6.6
Elements, comparable III.1.12
empty function II.3.4
Empty set II.1.7 R.1.8
Empty word I.App.1
Endowed with a structure IV.1.4
Endpoints of an interval III.1.13 R.6.4
Eq (X,Y), Card (X) III.3.1
equal I.5.1
Equalitarian theory I.5.1
Equality, relation of I.5.1 R.1.6
equation I.5.2
Equipotent sets III.3.1 R.7.1
Equivalence class II.6.2 R.5.2
Equivalence relation II.6.1 R.5.2
Equivalence relation on a set II.6.1
Equivalence relation, associated with a function II.6.2
Equivalence relation, coarser II.6.7
Equivalence relation, finer II.6.7
Equivalence relation, induced II.6.6
Equivalence relation, product II.6.8
Equivalence relation, quotient II.6.7
Equivalence, on a set II.6.1
Equivalent axioms R.8.4
Equivalent elements II.6.1
Equivalent powers R.7.2
Equivalent relations I.3.5 R.1.3
Equivalent species of structures IV.1.7
Equivalent theories I.2.4
Euclidean division III.5.6
Even integer III.5.6
Existential quantifier I.4.1
Expansion of an integer to base b III.5.7
Explicit axiom I.2.1
exponentiation R.4.9
Extension of a correspondence or mapping to sets of subsets II.5.1 R.2.4
Extension of a family of functions to product sets II.5.7
Extension of a mapping II.3.5 R.2.13
Extension of an ordering, order relation, preordering, preorder relation III.1.4 R.6
Extension of several mappings to the product sets R.3.14
Extension of two functions to product sets II.3.9
Extension, canonical IV. 1.2
Extension, inverse (of a mapping to sets of subsets) R.2.6
Extent, axiom of II.1.3
f(X) (X a subset) R.2.4
f(x), 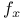 (f a function), F(x), (f a function), F(x),  (F a functional gaph) II.3.4 (F a functional gaph) II.3.4
f(x), 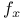 , ,  (f a mapping, x an element) R.2.2 (f a mapping, x an element) R.2.2
f(x,y), f(.,y), f(x,.), f( ,y), f(x, ) II.3.9
f:  , ,  II.3.4 II.3.4
Factor, of a product II.2.2 II.5.3
Factor, of an integer III.5.6
Factorial n III.5.8
Factorization of a mapping R.2.11
Factorization, canonical R.5.3
Factors, of a product set R.3.1 R.4.9
False relation I.2.2
Family II.3.4
Family of elements of a set II.3.4 R.2.14
Family of mutually disjoint sets II.4.7
Family of subsets of a set II.3.4
Family of subsets, decreasing (increasing) III.1.5
Family, double II.3.4
Family, finite III.4.1
Final character (of a totally ordered set) III.6.Ex.16
Final segment of a word I.App.1
Final structure IV.2.5
Finer covering II.4.6
Finer preordering III.1.4
Finer relation II.6.7
Finer structure IV.2.2
Finite cardinal III.4.1
Finite character (property of, set of subsets of) III.4.5 R.6.11
Finite family III.4.1
Finite sequence, finite sequence of elements of a set III.5.4 R.7.8
Finite set IV.4.1
First coordinate of an ordered pair II.2.1
First projection of a graph II.3.1
First species I.1.3
First term of a sequence III.5.4
Fixed element II.3.4 R.2.3
Formative construction I.1.3
Formative criterion I.1.4
Free subset of an ordered set III.1.Ex.5
Function see "Mapping"
Function of several variables R.3.13
Function of two arguments II.3.9
Function, characteristic III.5.5
Function, coordinate II.3.6 II.5.3
Function, defined on A with values in B II.3.4
Function, not depending on x II.3.9
Functional graph II.3.4
Functional relation I.5.3 R.2.1
Functional symbol I.5.3
G<X>, G(X), G(x) (G a graph, X a set, x an object) II.3.1
General solution I.5.2
General term (of a sequence) R.7.8
Generalized Continuum Hypothesis III.6.4
Generic element (of a set) R.1.2
Generic Structure IV.1.4
gf (g,f mappings) (by abuse of language) II.3.7
Graph II.3.1
Graph of a correspondence II.3.1
Graph of a mapping R.3.5
Graph of a relation II.3.1 R.3.2
Graph symmetric II.3.2
Graph, functional II.3.4
Graph, inverse II.3.2
Graphs, composition of II.3.3
greater III.1.3 R.6.3
Greatest element of an ordered set III.1.7 R.6.5
Greatest lower bound III.1 R.6.7
Half-open interval III.1.13 R.6.4
Hypothesis, auxiliary I.3.3
Hypothesis, continuum III.6.4
Hypothesis, generalized continuum III.6.4
Hypothesis, inductive III.2.2 III.4.3
Identification R.8.5
Identity R.1.3
Identity correspondence II.3.3
Identity mapping II.3.4 R.2.3
Image of a covering II.4.6
Image of a function (by abuse of language) R.2.4
Image of a set II.3.2
Image of a set under a correspondence II.3.1
| Image of a set under a function II.3.4 R.2.4
Image of a set under a graph II.3.1
Image of an equivalence relation II.6.6
Image, direct (of a structure) IV.2.6
Image, inverse (of a set under a mapping) R.2.6
Image, inverse (of a structure) IV.2.4
Implicit axiom I.2.1
IMPLY R.1.3
Inaccessible cardinal III.6.Ex.22
Inaccessible initial ordinal III.6.Ex.16
Inclusion relation II.1.2 III.1.1 R.1.2
Inconsistent axioms R.8.6
Increasing family of subsets III.1.5 R.6.12
Increasing mapping III.1.5 R.6.12
Indecomposable ordinal III.2.Ex.16
Independent (of other axioms) I.2.Ex.1
Index set of a family II.3.4 R.2.2
Indicial notation R.2.2
Induced equivalence relation R.5.5
Induced mapping II.6.5
Induced ordering, order relation, preordering, preorder relation III.1 R.6.1
Induced relation II.6.3
Induced structure IV.2.4
Induction, descending III.4.3
Induction, Noetherian III.6.5
Induction, Principle of III.2.2 III.4.3
Induction, restricted III.4.3
Induction, starting at k III.4.3
Induction, transfinite III.2.2
Inductive hypothesis III.2.2 III.4.3
Inductive set III.2.4 R.6.9
Infimum III.1.9 R.6.7
Infinite sequence III.6.1 R.7.8
Infinite set III.6.1
Infinity, axiom of III.6.1
Initial ordinal III.6.Ex.10
Initial segment of a word I.App.1
Initial structure IV.2.3
Injection II.3.7 R.2.8
Injection, canonical II.3.7
Injective mapping II.3.7 R.2.8
Integer, natural III.4.1
Integral part of the quotient of two integers III.5.6
Intersecting subsets R.1.13
Intersection of a family of sets, or subsets II.4.1 R.4.6
Intersection of a set of sets II.4.1
Intersection of several sets R.1.13
Intersection, countable R.7.9
Intervals (closed, half-open, open, unbounded) III.1.13 R.6.4
Intransitive II.6.Ex.11
Intrinsic term IV.1.6
Invariant element R.2.3
Inverse extension of a mapping R.2.6
Inverse image R.2.6
Inverse image of a covering II.4.6
Inverse image of a set II.3.2
Inverse image of a structure IV.2.4
Inverse image of an equivalence relation II.6.6
Inverse isomorphisms IV.1.5
Inverse limit, of a family of mappings III.7.2 R.6.14
Inverse limit, of a family of sets III.7.1 R.6.14
Inverse system, of mappings III.7.2 R.6.14
Inverse system, of sets III.7.1 R.6.14
Inverse system, of subsets III.7.2
Inverse, of a (bijective) mapping II.3.7 R.2.9
Inverse, of a correspondence II.3.2
Inverse, of a graph II.3.2
Involutory permutation II.3.7 R.2.9
Irreducible element (of a lattice) III.4.Ex.7
Isomorphic sets IV.1.5
Isomorphic structures IV.1.5 R.8.6
Isomorphism IV.1.5 R.8.6
Isomorphism of ordered sets III.1.3
Iterates of a mapping III.6.2 R.2.11
K(X) (K a subset of  , X a subset of E) R.3.6 , X a subset of E) R.3.6
K(x) (K a subset of  , x an element of E) R.3.9 , x an element of E) R.3.9
Larger than III.1.3
Last term of a finite sequence III.5.4
Lattice III.1.11 R.6.8
Lattice, Boolean III.1.Ex.17
Lattice, complete III.1.Ex.11
Lattice, distributive III.1.Ex.16
Lattice, relatively complemented III.1.Ex.17
Least element of an ordered set III.1.7 R.6.5
Least upper bound III.1.9 R.6.7
Least upper bound of a family of cardinals III.3.2
Left directed set III.1.10 R.6.8
Left inverse (of an injection) II.3.8
Left-hand endpoint of an interval III.1.13
Legitimation, theorem of I.3.3
Lemma I.2.2
Lemma, Zorn's III.2.4 R.6.10
Length, of a finite sequence III.5.4
Length, of a word I.App.1
Less than III.1.3 R.6.3
Lexicographical order relation, ordering III.2.6
Lexicographical product III.2.6 III.2.Ex.10
Limit, direct III.7.5 R.6.13
Limit, inverse III.7.1 R.6.14
Linearly ordered see "Totally ordered"
Link I.1.1
Logical components of a relation I.App.Ex.6
Logical construction I.App.Ex.6
Logical sign I.1.1
Logical theory I.3.1
Logically constructed I.App.Ex.6
Logically irreducible I.App.Ex.6
Lower bound III.1.8 R.6.7
Lower bound, greatest III.1.9 R.6.7
Mapping R.2.1
Mapping of a set into a set II.3.4
Mapping of a set onto a set II.3.7
Mapping, bijective II.3.7 R.2.9
Mapping, bounded above (bounded below, bounded) III.1.8 R.6.7
Mapping, compatible with an equivalence relation II.6.5
Mapping, compatible with two equivalence relations R.5.8
Mapping, composite II.3.7 R.2.11
Mapping, constant II.3.4 R.2.3
Mapping, decreasing III.1.5 R.6.12
Mapping, diagonal II.3.7 II.5.3 R.3.4
Mapping, empty II.3.4
Mapping, identity II.3.4 R.2.3
Mapping, increasing III.1.5 R.6.12
Mapping, injective II.3.7 R.2.8
Mapping, inverse II.3.7 R.2.9
Mapping, monotone III.1.5
mapping, one-to-one II.3.7 R.2.9
Mapping, order-preserving III.1.5
Mapping, order-reversing III.1.5
Mapping, partial II.3.9 R.3.13
Mapping, strictly decreasing (strictly increasing, strictly monotone) III.1 R.6.12
Mapping, surjective II.3.7 R.2.4
Mapping, universal IV.3.1
Mappings, agreeing on a set II.3.5
Mappings, canonical see "Canonical"
Mathematical theory I.1.1 I.2.1 I.2.2
Maximal element II.1.6 R.6.7
Maximum R.6.5
Membership, relation of II.1.1 R.1.10
Method, of disjunction of cases I.3.3
Method, of reductio ad absurdum I.3.3
Method, of the auxiliary constant I.3.3
Method, of the auxiliary hypothesis I.3.3
Minimal element III.1.6 R.6.6
Minimum R.6.5
Mobile (set of finite subsets) III.4.Ex.11
Model of a theory I.2.4
Monotone mapping III.1.5
Morphism IV.2.1
Multiple of an integer III.5.6
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



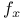 (f a function), F(x),
(f a function), F(x),  (F a functional gaph)
(F a functional gaph)  (f a mapping, x an element)
(f a mapping, x an element)  ,
, 
 , X a subset of E)
, X a subset of E)