|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Barwise J. (ed.) — Handbook of Mathematical Logic |
|
|
 |
| Предметный указатель |
Spector — Gandy Theorem 276
Spector — Gandy Theorem, Abstract Version of 768
Spector, C. 276 636 637 639 652 768 771
Spector, C., 782 953 954 968 1030 1038
Speed-up theorem 539
Splitting theorem 663f
Square ( ) Principle of Jensen 479 ) Principle of Jensen 479
Square ( ) Principle of Jensen, Consistency of 434f ) Principle of Jensen, Consistency of 434f
St(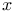 ) 203 ) 203
Stable Ordinal 246
Stable theory 87 164 173 192
Stage Comparison Partial Function 696
Stage Comparison Theorem 697 766
Stages (for Constructing Sets) 323
Stages of an Inductive Definition 758
Standard Codes 478
Standard part 203 215
Standard representation 1003
State 530
Stationary Set of Ordinals 372f 407
Statman, R. 871 897
Steele, J. 633 812 956
Steinetz 131 147 609
Steinhaus, H. 813
Steinitz Theorems 147 149
Stephenson, R.M. 508 522
Stewart, F.M. 429 430 642 643 807 808 814
Stillwell, J. 656
Stockmeyer, L. 624
Stone Space of a Language 59
Stone Space over a Model 84
Stone, A.H. 60 84 85 86 357 501 647
Stout, L.N. 310
Strategy 643
Strong Relation Universality 267
Strong, H. 950 1093
Stroyan, K.D. 197 206 207 211 215 217 221
Structure 17 (see also “Model)
Structure Induced by an Interpretation 613
Sturm, J.C.F. 148 149 152
Sturm’s Theorem 148
sub 826 836f
Subformula 95
Subformula property 876
Subobject classifier 1068
Substructure (Subsystem) 52 184
Subsystem see “Substructure
Suitable Class 685
Sullivan, K. 207
Superjump 735
Superstable theory 87
Superstructure 200
Support 237 361
Suslin hypothesis 472 484
Suslin Line 378
Suslin property see “CC Spaces”
Suslin Quantifier 695
Suslin, M.I. 233 235 236 264 272 276 341 378 379 384 385 386 390 453 472 473 474 475 476 484 485 493 494 499 505 507 510 559 566 668 785 792 794 798 811 813 815
Suszko, R. 63 102 142 156 157
Svenonius, L. 81 261 282
Swierczkowski, S. 807 808 813
Symbol 7
Symmetric extension 360 362
Systems of Notations for Ordinals see “Ordinal Notations”
Szabo, M.E. 310
Szmielew, W. 611
T-predicate 537 541
Tait, W.W. 265 869 871 899 900 902 949
Tait, W.W., 957 958 959 960 961 966 1036 1102
Taitskin 172
Takahashi, S. 310
Takeuti, G. 654 656 657 672 675 679 957
Takeuti, G., 1042 1055
Tall, F.D. 507
Tarski, A. 6 48 52 53 54 55 62 63 65 67
Tarski, A., 119 131 140 143 145 146 147 152 156 179 235 351 352 353 356 367 375 596 606 607 608 609 618 629 671 844 847
Tarski’s Decidability Theorem for the Reals 596 606 609 624
Tarski’s Undefinability Theorem 558 (see also “Truth in Arithmetic”)
Tautology of Propositional Logic 25
Tautology of Propositional logic, of First-Order Logic 28
Taylor, W. 216 222 223 225
Taylor’s Small Oh Formula 216
TC see “Transitive Closure”
Tennenbaum, S. 445 446
Terjanian, G. 132 151 152
Term of Forcing Language 413
Term, closed 18
Term, Skolem 185
Theory 50
Theory of a Class K 50
Theory, complete 16
Theory, consistent 16
Theory, decidable 16
Thiele, E. — J. 309
Thomason, S.R. 637 646 647
Thompson, R.J. 578
Thue Processes 575
Thue, A. 571 572 575 576 577 580
Tierney 299 310 1055 1071
Topology, Unsolvable Problems in 579f
Topos 298 1054 1068
Total function 528
Totally transcendental 84
Transfinite Induction Scheme 942 (see also “Induction”)
Transition function 531
Transitive closure 242
Transitive Collapse see “Mostowski Collapsing Lemma
Transitive Set Object 309
Transitive Sets and Models 405f
Transitivity theorem 559
TREE 381f 407 472 Suslin
Tree Decidability Theorem 616
Troelstra, A.S. 819 871 891 973 974 980 981 982 985 990 991 992 993 1009 1013 1014 1015 1019 1020 1021 1026 1027 1030 1032 1040 1042 1093
Truncation Lemma 248
Truth (in Arithmetic) 558 560 639 647
Truth Assignment (for Propositional Logic) 24
Truth, definition 843
Truth, Lemma 415
Truth, Set of Arithmetic 639 647
Truth, table 24
Tugu 656 657 692 735 737 656 657 692 735 737
Tugu Object 692 Object 692
Turing machine 530f 569f 587 590f
| Turing machine, universal 536
Turing Machine, Value Category 286
Turing Machine, Vaught Covering Theorem 271
Turing Machine, Vaught Formula 254
Turing Machine, Vaught Reduction Theorem 276
Turing Machine, Vicious Circle Principle see Circular Reasoning”
Turing reducibility 550 633
Turing, A. 528 530 531 532 533 534 535 536 537 538 539 540 541 542 543 547 548 549 550 552 553 554 562 566 587 599 632 633 669
Two-cardinal Models 68
Two-cardinal Theorems 68 487
Tychonoff, A. 27 28 350 356 618
TYPE 76 127
Type of a point 707
Type,  Family of 266 Family of 266
Type, (Definable) 1064
Type, Symbols 929
Ulam Matrix 376
Ulam, S. 375
Ullman, J. 584
Ulm 97
Ulmer, F. 287 289 290 291 292
Ultrafilter 107
Ultrafilter, good 134
Ultrafilter, principal 108
Ultrapower 109
Ultraproduct 109f
Ultraproduct of Rings 110
Uncountability Quantifier 44
Undecibable Theory 16 548 597
Unfruitful Limitations on Mathematics 330
Uniformization theorem 368 803
Uniformly continuous 206
Uniformly differentiable 206 208
Union axiom 326
Uniqueness Theorem for Basic Saturated Models 75 76
Uniqueness Theorem for Prime Models 80
Universal formula 52
Universal function 702
Universal R.E. Relation 543
Universal set 788
Universal System 705 715
Universal theory 53
Universal Turing machine 536
Universes of Sets and Functions 918
Universes of Sets and Functions, 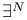 -closed 921 -closed 921
Universes of Sets and Functions,  -closed 921 -closed 921
Universes of Sets and Functions, Cartesian Closed 921
Unsecured Sequences, Induction over 1009
Unsolvable problems 534 538 545 548
Unstable theory 87
Upward L wenheim — Skolem Theorem 65 wenheim — Skolem Theorem 65
Urelement 237 322
V = L see “Constructibility Axiom
Valid 29
Validity (Intuitionistic) 1024f
Vaught, R.L. 53 55 63 65 66 67 68 69 73 77 79 80 81 100 103 135 140 141 143 233 237 254 255 256 257 259 261 262 271 272 274 275 276 282 487 607 608 609 612 628
Verdier, J.L. 1055 1088
Vesley, R.E. 994 1010 1018 1023
Vitali 352 365 784
Volger, H. 293 295 1087
W-Principle of Silver 514
W-Principle of Silver, Consistency of 432f
Wadge, W. 633 812
Wadsworth, C.P. 117 1121 1125 1126 1127 1128
Waerden, B.L. van der 563
Wagner, E.G. 950 1093
Wainer, S. 735
Wang, H. 548 588
Waskiewicz, J. 174
Weak  -recursiveness 660 -recursiveness 660
Weak Counterexample 996
Weak Robinson Forcing 90
Weakly compact cardinals 397 483
Weglorz, B. 174
Wehrfritz, B.A.F. 120
Weierstrasz, K. 198 206 550 1042 1043 1045
Weierstrasz’ Approximation Theorem 1045
Weiss, W. 508
Weisspfenning, V. 142 152 173
Well Ordered Model 193
Well-founded of Orderings 941
Well-founded Part 247
Well-founded relation 305 743
Well-founded Structure 246
Well-founded Tree 747
Well-founded, Length of 792
Well-ordering theorem 347
Well-orderings 96
Well-orderings of 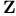 946 958 946 958
Well-orderings of Ramified Analysis 959
Well-orderings, Comparability of 945 954
Well-orderings, Natural 878
Well-orderings, Provably Recursive 945
Western Model Theory 48
Weyl, H. 217 822 823 825 926 975
Wheeler, W.H. 142 167 168 170 171 172
Whitehead, A.N. 6 494 495
Whitehead’s Problem 494
Winkler, P. 164
Witnessing Constants 30
Witnessing Expansion 29
Wood, C. 162 165 167 174
Word problem 169 171
Word Problem  -group 151 -group 151
Word problem for groups 578
Word Problem for Semigroups 577
Wraith, G.C. 288 304 310
Yasuhara, A. 528 580
Yates, C.E.M. 632 637 641 645 646 647 672
Yoneda, N. 288
Zariski Topos 302 307
Zariski, O. 127 302 307
Zermelo — Fraenkel Axioms for Set Theory 324f 404 840 851
Zermelo, E. 15 51 55 194 237 309 347 348 404 410 416 454 547 637 784 808 822 823 840 917 1071 1092
ZF see “Zermelo — Fraenkel Axioms for Set Theory
ZFC see “Zermelo — Fraenkel Axioms for Se Theory
Ziegler 153 171
Zilber, B.I. 164
ZO Set Theory 309
Zorn 107 338 354 355 356 379 419
Zorn, 446 636
Zorn’s Lemma 338 355
Zucker, J. 779 968 1091
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ) Principle of Jensen
) Principle of Jensen 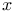 )
) 
 Family of
Family of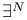 -closed
-closed -closed
-closed  wenheim — Skolem Theorem
wenheim — Skolem Theorem  -recursiveness
-recursiveness 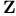
 -group
-group