|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bourbaki N. — Algebra I: Chapters 1-3 |
|
|
 |
| Предметный указатель |
Product group, internal product group, of a family of quotient groups I § no.
Product magma I § no.
Product of 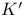 -structures II § no. -structures II § no.
Product of an operator and an element I § no.
Product of an ordered sequence I § no.
Product of laws of composition I § no.
Product of matrices calculated according to a mapping II § no.
Product of matrices calculated in a ring II § no.
Product of modules II § no.
Product of multimodules II § no.
Product of two elements I § no.
Product of two-sided ideals I § no.
Product ring I § no.
Product, (right, left) inner III § nos.
Product, block, of matrices II § no.
Product, crossed III § Exercise
Product, exterior, of p-vector and a q-vector III § no.
Product, external semi-direct, of G by F relative to 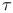 I § no. I § no.
Product, fibre, of groups with operators I § no.
Product, fibre, of modules II § Exercise
Product, free, of algebras III § Exercise
Product, free, of groups I § no.
Product, graded tensor, of graded algebras III § nos.
Product, graded tensor, of two graded modules II § no.
Product, internal direct, direct product, product, of subgroups I § no.
Product, symmetric, of multilinear mappings III § no.
Product, tensor, of a family of  -modules relative to a triple (n, p, q) II § no. -modules relative to a triple (n, p, q) II § no.
Product, tensor, of algebras III § no.
Product, tensor, of an infinite family of algebras III § no.
Product, tensor, of bases of algebras III § no 5
Product, tensor, of cogebras III § no.
Product, tensor, of two bases II § no.
Product, tensor, of two elements II § no.
Product, tensor, of two linear mappings II § no.
Product, tensor, of two matrices over a commutative ring II § no.
Product, tensor, of two modules II § no.
Product, tensor, of two multimodules II § no.
Product, tensor, of two semi-linear mappings II § no.
Projection homomorphism I § no.
Projective field II § no.
Projective group II § no.
Projective hyperplane, plane II § no.
Projective line II § no.
Projective mapping II § no.
Projective module II § no.
Projective space II § nos.
Projectively free, projectively related, family II § no.
Projector II § no.
Pseudo-ring I § no.
Pseudo-ring with zero square I § no.
Pseudomodule, left, right II Appendix no.
Pure p-vector III § no.
Pure quaternion III § Exercise
Quadratic algebra III § no.
Quasi-group I § Exercise
Quaternion algebra III § no.
Quaternion, pure III § Exercise
Quaternionic group I § Exercise
Quotient algebra III § no 2
Quotient graduation II § no.
Quotient group with operators I § no.
Quotient law I § no.
Quotient magma I § no.
Quotient module, vector space II § no.
Quotient multimodule II § no.
Quotient of an action I § no.
Quotient ring I § no.
Quotients of a composition series of a group with operators I § no.
Rank of a free group I § Exercise
Rank of a linear mapping of vector spaces II § no.
Rank of a linear system over a field II § no.
Rank of a matrix over a field II § no.
Rank of a semi-linear mapping of vector spaces II § no.
Rank of a subset of a module over an integral domain II § no.
Rank of a subset of a vector space II § no.
Rank of an affine linear mapping II § no.
Rank of an element in a tensor product of vector spaces II § no.
Ratio of a homothety II § no.
Rational integer I § no.
Rational number I § no.
Rational numbers, field of I § no.
Rational over a subfield (linear form) II § no.
Rational over a subfield (linear mapping) II § no.
Rational over a subfield (subspace, vector) II § no.
Reduced decomposition of an element of an amalgamated sum I § no.
Reflexive module II § no.
Regular, left regular, right regular, element I § no.
Related system, subset II § no. and no.
Relation, equivalence, compatible with a law of composition I § no.
Relation, equivalence, compatible with an action I § no.
Relation, equivalence, generated by a family of ordered pairs I § no.
Relation, equivalence, left, right, compatible with a law of composition I § no.
Relations, commutativity, in a multiplication table III § no.
Relations, Grassmann III § no.
Relations, module of linear II § no.
Relatively prime integers I § no.
Relator I § no. § no.
Relator, universal III § no.
Relators of a presentation I § no. § no.
Relators, ideal of III § no.
Relators, polynomial III § no.
Residually finite group I § Exdrcise
Residue of a semi-group I § Exercise
Restricted algebra of a monoid III §2 no.
Restricted sum of groups I § no.
Restricted sum of groups with respect to subgroups I § no.
Restricted sum, internal I § no.
Restriction of scalars (algebra obtained by) III § no.
Resulting (element) from substituting elements for indeterminates I § no.
Retraction of an extension I § no.
Right hand side of a linear equation, right hand sides of a linear system II § no.
Ring I §8 no.
Ring (graded, graded with positive degrees, bigraded) II § no.
Ring obtained by the adjunction of a unit element II Appendix no.
Ring of endomorphisms of a commutative group I § no.
Ring of fractions with denominators in S I § no.
Ring of integers modulo n I § no.
Ring of polynomials which are not commutative relative to an endomorphism and a derivation III § Exercise
Ring, boolean I § Exercise
Ring, commutative I § no.
Ring, graded quotient II § no.
Ring, opposite I § no.
Ring, product I § no.
Ring, quotient I § no.
Ring, total, of fractions I § no.
Ring, zero I § no.
Row of a matrix II § no.
Rule, sign I § no.
S-neighbouring element I § Exercise
scalar II § no.
Scalar linear equation II §2 no.
Scalar matrix II § no.
Schreier's Theorem on composition series I § no.
Section of an extension I § no.
Semi-direct product of groups I § no.
Semi-group, left, right I §2 Exercise
Semi-homomorphism, algebra, algebra p-homomorphism III § no.
Semi-linear mapping II § no.
Sequence, exact II § no.
Sequence, ordered I § no.
Sequence, split exact II § no.
Sequences, similar ordered I § no.
Series, algebra of formal power III § no.
Series, composition I § no.
Series, derived I § no.
Series, equivalent decomposition I § no.
Series, finer composition I § no.
Series, formal power III § no.
Series, Jordan-Holder I §4 no.
Series, lower central I § no.
| Series, normal I § Exercise
Series, principal I § Exercise
Set of degrees of a graded group II § no.
Set of subgroups satisfying the maximal condition, the minimal condition I § Exercise
Set, generating, of a group I § no.
Set, generating, of a magma I § no.
Sets, orthogonal II § no.
Shift, shifting II § no.
Sign of a rational number I § no.
Signature of a permutation I § no.
Similar endomorphisms III § Exercise
Similar matrices II § no.
Similar ordered sequences I § no.
Simple group I § no.
Simply transitive operation I § no.
Skew field I § no.
Skew graded bigebra III § no.
Skew tensor product of graded algebras III § nos.
Skew-symmetric tensor III § no.
Skew-symmetrized tensor III § no.
Solution of a linear equation, of a linear system II § no.
Solution, trivial, zero solution of a homogeneous linear equation II § no.
Solvable group, solvable group of class n I § no.
Space, affine, attached to a vector space II § no.
Space, canonical projective, associated with a vector space II § no.
Space, projective II § nos.
Space, projective, derived from a vector space II § no.
Space, quotient vector, quotient space II § no.
Space, right, left, vector, over a field II § no.
Space, vector, associated with a module over an integral domain II § no.
Space, vector, obtained by taking an origin in an affine space II § no.
Space, vector, of translations of an affine space II § no.
Split exact sequence II § no.
Stabilizing (operator, set of operators) a subset I § no.
Stabilizing, strictly (operator, set of operators), a subset I § no.
Stable subgroup of a group with operators I § no.
Stable subset I § no.
Strict stabilizer I § no.
Strict transporter I § no.
Strictly negative, strictly positive, rational integer I § no.
Strictly negative, strictly positive, rational number I § no.
Strictly stabilizing a subset I § no.
Strongly associative subset III Appendix no.
Structure, projective space II §9 no.
Structures, module (multimodule), compatible II § no.
Subalgebra III § no.
Subalgebra generated by a subset III § no.
Subalgebra, graded III § no.
Subfield I § no.
Subfield generated by a subset I § no.
Subgroup, characteristic I §5 no.
Subgroup, invariant stable, invariant subgroup I § no.
Subgroup, normal stable, normal subgroup I § no.
Subgroup, stable subgroup I § no.
Subgroup, stable, generated by a subset I § no.
Subgroup, Sylow, Sylow p-subgroup I § no.
Submagma I § no.
Submagma, unital I § no.
Submagma, unital, generated by a subset I § no.
Submagna generated by a subset I § no.
SubMatrix II § no.
Submodule II § no.
Submodule generated by a family II § no.
Submodule, component, of a direct sum of modules II § no.
Submodule, graded II § no.
Submodule, irreducible II §2 Exercise
Submodule, orthogonal (or totally orthogonal) to a subset of E (resp. E*) II § no.
Submodule, torsion, of a module over an integral domain II § no.
Submodule, zero II § no.
Submodules, supplementary II § no.
Submultimodule II § nos.
Subring I § no.
Subring generated by a subset I § no.
Subring, graded II § no.
Subset centralizing a subset I § no.
Subset normalizing a subset I § no.
Subset, affine II § no.
Subset, free, related subset II § no.
Subset, homogeneous, of degree p with respect to certain indeterminates in a formal power series III § no.
Subset, stable I § no. no.
Subset, stable, generated by a subset I § no. no.
Subset, strongly associative III Appendix no.
Subset, symmetric I §4 no.
Subsets, conjugate I § no.
Subspace associated with a homogeneous element of the symmetric algebra III § no.
Subspace associated with a homogeneous element of the tensor algebra III § no.
Subspace rational over a subfield II § no.
Subspace, vector, subspace II § no.
Subspaces associated with a homogeneous element of the exterior algebra III § no.
Subspaces associated with an element of a tensor product of vector spaces II § no.
Sum of a family of elements of finite support I § no.
Sum of a family of left ideals, of right ideals I § no.
Sum of a family of submodules II § no.
Sum of an ordered sequence I § no.
Sum of two elements I § no.
Sum of two matrices II § no.
Sum, amalgamated, of modules II § Exercise
Sum, amalgamated, of monoids II § no.
Sum, direct I § no.
Sum, direct, of a family of submodules II § no.
Sum, external direct, of a family of submodules II § no.
Sum, internal restricted, of subgroups I § no.
Sum, monoidal I § no.
Sum, restricted, of groups with respect to subgroups, restricted sum of groups I § no.
Supersolvable group I § Exercise
Supplementary submodules II § no.
Support of a cycle I § no.
Support of a family I § no.
Suppress columns, rows, in a matrix II § no.
Sylow subgroup I § no.
Symbol, Kronecker II § no.
Symmetric algebra of a module III § no.
Symmetric group I § no.
Symmetric multilinear mapping III § no.
Symmetric power of a linear mapping III § no.
Symmetric power of a module III § no.
Symmetric product of two multilinear mapping III § no.
Symmetric subset in a group I § no.
Symmetric tensor III § no.
Symmetrization of a tensor III § no.
System of equations of a vector subspace II § no.
System of factors III § Exercise
System of homogeneous coordinates of a point II § no.
System of linear equations, linear system, homogeneous linear system II § no.
System, direct, of graded algebras III § no.
System, direct, of magmas I § no.
System, direct, of modules II § no.
System, direct, of rings (groups, fields) I § no.
System, free, related system II § no.
System, generating, of a group I § no.
System, generating, of a magma I § no.
System, generating, of a module II § no.
System, generating, of a projective space II § no.
System, generating, of a unital magma I § no.
System, generating, of an algebra III § no.
System, inverse, of algebras III § no.
System, inverse, of magmas II § no.
System, inverse, of modules II § no.
System, inverse, of rings (groups, fields) I § no.
System, trivial, of commutation factors III § no.
Table, diagonal, lower triangle, upper triangular, of matrices II § no.
Table, multiplication, of an algebra III § no.
Table, square, of matrices II § no.
Tensor algebra of a module III § no.
Tensor of type (i, j) III § no.
Tensor, contravariant, covariant tensor, mixed tensor III § no.
Tensor, skew-symmetric III § no.
Tensor, symmetric III § no.
Tensorial power of a linear mapping III § no.
Tensorial power of a module III § no.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



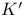 -structures
-structures 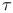
 -modules relative to a triple (n, p, q)
-modules relative to a triple (n, p, q)