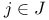|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bourbaki N. — Algebra I: Chapters 1-3 |
|
|
 |
| Предметный указатель |
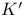 -structure on a vector K-space II § no. -structure on a vector K-space II § no.
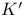 -structure, induced II § no. -structure, induced II § no.
 -structure, product II § no. -structure, product II § no.
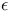 -derivation of a graded algebra, -derivation of a graded algebra, 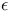 -derivation of a ring III § no. -derivation of a ring III § no.
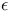 -derivation, inner III § no. -derivation, inner III § no.
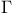 -morphism ( -morphism (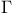 a set of operators) I § no. a set of operators) I § no.
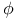 -homomorphism I § no. -homomorphism I § no.
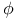 -morphism ( -morphism (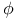 a homomorphism of one monoid of operators into another) I §5 no. a homomorphism of one monoid of operators into another) I §5 no.
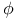 -morphism ( -morphism (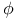 a mapping of one set of operators into another) I § no. a mapping of one set of operators into another) I § no.
(K, 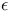 )-derivation of degree )-derivation of degree 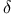 , , 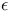 -derivation of degree III §10 no. -derivation of degree III §10 no.
Abelian group I § no.
Absolute value of a rational number I § no.
Action of one set on another I § no.
Action, canonical I § no.
Action, distributive I § no.
Action, induced I § no.
Action, quotient I § no.
Action, right, left, derived from a law of composition I § no.
Actions which commute I § no.
Addition I § no.
Addition of rational integers I § no.
Additively (law written) I § no.
Adjoint of a matrix III § Exercise
Adjunction of a unit element (algebra derived by) III § no.
Affine function II § no.
Affine group II § no.
Affine line, plane, hyperplane II § no.
Affine mapping II § no.
Affine space II § no.
Affine subset, linear variety II § no.
Affinely free, affinely related family II § no.
Affinely independent points II § no.
Algebra derived from an algebra by the adjunction of a unit element III § no.
Algebra generated by generators subject to relations III § no.
Algebra obtained by extension of scalars III § no.
Algebra obtained by restriction of scalars III § no.
Algebra of a group, of a magma, of a monoid III § no.
Algebra of dual numbers III § no.
Algebra of formal power series III § no.
Algebra of Hamiltonian quaternions III §2 no.
Algebra of octonians of type ( , , 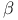 , , 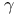 , , 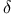 ) III Appendix no. ) III Appendix no.
Algebra of quaternions III § no.
Algebra of quaternions of type ( , , 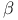 , , 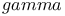 ), of type ( ), of type ( , , 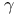 ) III § no. ) III § no.
Algebra, A-Algebra III § no.
Algebra, alternating graded III § no.
Algebra, alternative III Appendix no.
Algebra, anticommutative graded III §4 no.
Algebra, associative III § no.
Algebra, Cayley III § no.
Algebra, commutative III § no.
Algebra, exterior, of a module III § no.
Algebra, free III § no.
Algebra, free associative III § no.
Algebra, free associative and commutative III § no.
Algebra, free, of a module III § Exercise
Algebra, graded, over a graded ring III § no.
Algebra, opposite III § no.
Algebra, product III § no.
Algebra, quadratic III § no.
Algebra, quadratic, of type ( , , 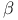 ) III § no. ) III § no.
Algebra, quotient III § no.
Algebra, Rees III § Exercise
Algebra, restricted, of a monoid III § no.
Algebra, symmetric, of a module III § no.
Algebra, tensor, of a module III § no.
Algebra, total, of a monoid III §2 no.
Algebra, unital III § no.
Algebra, universal unital associative, defined by a generating system related by a family of relators III § no.
Algebra, universal, defined by a generating system related by a family of relators III §2 no.
Algebra, universal, generated by a set subjected to identities III § no.
Algebras, linearly disjoint III § no.
Alternating graded algebra III § no.
Alternating group III § no.
Alternating multilinear mapping III § no.
Alternative algebra III Appendix no.
Amalgamated sum I § no.
Annihilated by a scalar (element) II § no.
Annihilator, left, right I § no.
Annihilator, of a subset, of an element of a module II § no.
Antiautomorphism III § no.
Anticocommutative graded cogcbra III § no.
Anticocommutative skew graded bigebra III §11 no.
Anticommutative graded algebra III § no.
Anticommutative skew graded bigebra III § no.
Antiderivation, K-antiderivation III § no.
Antiendomorphism of a ring II § no.
Associated (B-module) with an A-module and a ring homomorphism A —> A II § no.
Associated (faithful module) with a module II § no.
Associated (law of action) with an action I § no.
Associated (linear mapping) with an affine linear mapping II § no.
Associated (vector subspace) with a homogeneous element of a symmetric algebra III § no.
Associated (vector subspace) with a homogeneous element of a tensor algebra III § no.
Associated (vector subspace) with a homogeneous element of an exterior algebra III § no.
Associated (vectorspace) with a module over an integral domain II § no.
Associative algebra III § no.
Associative algebra, free III § no.
Associative and commutative algebra, free III § no.
Associative law I § no.
Associativity relations in a multiplication table III § no.
Associativity theorem I § no.
Associator III Appendix no.
Attached (affine space) to a vector space II § no.
Augmentation III § no.
Automorphism with no fixed point I § Exercise
Automorphism, inner of a group I § no.
Automorphism, inner, of a ring I § no.
Barycentre of m points, barycentre of a family of weighted points II §9 no.
Barycentric coordinate II § no.
Bases dual to one another II § no.
Basic family in a group I § no.
Basis 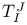 (M) associated with a basis of M III § no. (M) associated with a basis of M III § no.
Basis dual of a basis of a module II § no.
Basis of a module II § no.
Basis of an algebra III § no.
Basis of type ( , , 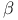 ) of a quadratic algebra III § no. ) of a quadratic algebra III § no.
Basis of type ( , , 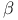 , , 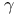 ), of type ( ), of type ( , , 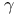 ), of a quaternion algebra III § no. ), of a quaternion algebra III § no.
Basis, Hamel II § no.
Basis, projective II §9 Exercise
Biadditive, Z-bilinear mapping II § no.
Bicentralizer I § no.
Bicentralizer of a subalgebra III § no.
Bicyclic group I § Exercise
Bidual of a module II § no.
Bigebra of a monoid III § no.
Bigebra, anticommutative, anticocommutative, skew graded III § no.
Bigebra, cocommutative, commutative, graded III § no.
Bigebra, graded bigebra, skew graded bigebra III § no.
Bigraded group, ring, module II § no.
Bigraduation II § no.
Bilinear mapping II § no.
Bimodule over algebras III § no.
Bimodule, (A, B)-bimodule II § no.
Binomial formula I § no.
Block product of matrices II § no.
Boolean ring I § Exercise
Bordered matrix II § no.
Bracket, 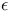 -bracket of two derivations III § no. -bracket of two derivations III § no.
C-multilinear mapping II § no.
Cancellable, left, right, cancellable, element I §2 no
Cartan — Brauer — Hua Theorem I § Exercise
Cayley algebra III § no.
Cayley extension of an algebra III § no.
Cayley norm, trace III § no.
Cayley octonians III Appendix no.
Cayley — Hamilton theorem III § no.
Central element I § no.
Central extension I § no.
Central homothety II § no.
Central ring homomorphism II § no.
Central series, lower I § no.
| centralizer I § no.
Centralizer of a subalgebra of an associative algebra III § no.
Centralizer of a subset I § no.
Centralizer of a subset of a field II § no.
Centralizer subalgebra III § no.
Centralizing element I § no.
Centralizing subset I § no.
Centre I § no.
Centre of a projective linear mapping II § no.
Centre of an algebra III § no.
Change of coordinates, formulae of II § no.
Characteristic of a field I § Exercise
Characteristic polynomial of a matrix III § no.
Characteristic subgroup I § no.
Class, conjugacy I § no.
Class, nilpotency, of a group I § no.
Class, solvability, of a group I § no.
Coassociative cogebra III § no.
Cocommutative bigebra III § no.
Cocommutative cogebra III § no.
Codiagonal mapping II § no.
Codimension of a vector subspace II § no.
Codimension of an affine linear variety II § no.
Coefficients of a formal power series III § no.
Coefficients of a linear combination II § no.
Coefficients of a polynomial III § no.
Coefficients of a system of linear equations II § no.
Cofactor of an element of a square matrix III § no.
Cogebra, A-cogebra III § no.
Cogebra, anticocommutative graded III § no.
Cogebra, coassociative III § no.
Cogebra, cocommutative III § no.
Cogebra, counital III § no.
Cogebra, graded III § no.
Cogebra, opposite III § no.
Coimage of a linear mapping II § no.
Coincidence group I § no.
Cokernel of a linear mapping II § no.
Column of a matrix II § no.
Combination, linear II § no.
Combinations, formal linear (module of) II § no.
Commutation factor III § no.
Commutative algebra III § no.
Commutative field I §9 no.
Commutative graded bigebra III § no.
Commutative group with operators I § no.
Commutative group, free, over X I § no.
Commutative law I § no.
Commutative magma I § no.
Commutative monoid, free, over X I § no.
Commutative ring I § no.
Commutativity relations in a multiplication table III § no 7
Commutativity theorem I § no.
Commutator group I § no.
Commutator of two elements I § no.
Commute, actions which I § 5 no.
Commute, elements which I § no.
Compatible (equivalence relation) with a law of composition I § no 6
Compatible (equivalence relation) with an action I § no.
Compatible (graduation) with a coproduct III § no.
Compatible (graduation) with a ring, module, structure II § no.
Compatible (graduation) with an algebra structure III § no.
Compatible (mapping) with an action I § no.
Compatible (mapping) with the operation of a monoid I § no.
Compatible law of composition and equivalence relation I § no.
Compatible module or multimodule structure II § no.
Compatible, left, right (equivalence relation), with a law of composition I § no.
Complementary minors III § no.
Component of an element in a direct sum II § no.
Component of an element with respect to a basis II § no.
Component submodule of a direct sum II § no.
Component, homogeneous, of an element in a graded group II § no.
Component, S-connected I § Exercise
Composition in M(X) I § no.
Composition of a family with finite support I § no.
Composition of an ordered sequence I § no.
Composition of the empty family I § no.
Composition of words I § no.
Composition series I § no.
Composition, law of I § no.
Condition, maximal (resp. minimal) (set of subgroups satisfying the) I § Exercise
Congruence modulo a rational integer I § no 10
Congruent (elements) modulo an ideal I § no.
Conjugacy class in a group I § no.
Conjugate elements in a group I § no.
Conjugate elements under the operation of a group I § no.
Conjugate subsets in a group I § no.
Conjugation, conjugate in a Cayley algebra III § no.
Conjugation, conjugate in a quadratic algebra III § no.
Constants of structure of an algebra with respect to a basis III § no.
Contraction of two indices in a mixed tensor III § no.
Contragradient of an isomorphism II § no.
Contragredient of an invertible square matrix II § no.
Contravariant tensor III § no.
Coordinate form II § no.
Coordinate of an element with respect to a basis II § no.
Coordinate, barycentric II § no.
Coordinates of a tensor over M with respect to a basis of M III § no.
Coordinates, homogeneous (system of), of a point in a projective space II § no.
Coproduct III § no.
Coset (right, left) modulo a subgroup I § no.
Cotranspose of an endomorphism III § no.
Counit III § no.
Counital cogebra III § no.
Covariant tensor III § no.
Cramer formulae, system III § no.
Cross-ratio II § Exercise
Crossed homomorphism I § Exercise
Crossed product III § Exercise
Cycle of a permutation I § no.
Cyclic group I § no.
Decomposable p-vector III § no.
Decomposition, direct, of a ring I § no.
Decomposition, reduced decomposition of an element in an amalgamated sum of monoids I § no.
Defined (group) by generators and relations I § no.
Defined (monoid) by generators and relations I § no.
Degree of a homogeneous element in a graded group II § no.
Degree of a polynomial with respect to the indeterminates 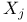 such that such that 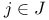 III § no. III § no.
Degree, total degree, of a monomial III § no.
Degree, total degree, of a polynomial III § no.
Degree, total degree, of an element of a free algebra, of a free associative algebra III § no.
Denominator I § no.
Derivation of a ring A into a ring A III § no.
Derivation, K-derivation III § no.
Derivative, partial III § no.
Derived (element) from an element of the free algebra by substituting elements for the indeterminates III § no.
Derived (element) from an element of the free associative algebra by substituting elements for the indeterminates III § no.
Derived (left action, right action) from a law of composition I § no.
Derived group of a group I § no.
Derived series of a group I § no.
Determinant of a matrix III § no.
Determinant of a sequence of vectors III § no.
Determinant of an endomorphism III § no.
Determinant, Cauchy III § Exercise
Determinant, Vandermonde III § no.
Diagonal elements of a square matrix II § no.
Diagonal matrix of matrices II § no.
Diagonal of a square matrix, diagonal matrix II § no.
Diagram, exact II § no.
Differences, group of I § no.
Differences, monoid of I § no.
Differential of an element III § no.
Dihedral group I § Exercise
Dilatation II § Exercise
Dimension of a free module II § no.
Dimension of a projective space II § no.
Dimension of a vector space II § no.
Dimension of an affine linear variety II § no.
Dimension of an affine space II § no.
Dimorphism II § no.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



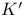 -structure on a vector K-space
-structure on a vector K-space 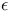 -derivation of a graded algebra,
-derivation of a graded algebra, 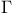 -morphism (
-morphism (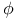 -homomorphism
-homomorphism 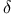 ,
,  ,
, 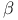 ,
, 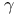 ,
, 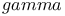 ), of type (
), of type ( (M) associated with a basis of M
(M) associated with a basis of M  such that
such that